关于 scikit-learn 实现规范化的方法详解

一、fit_transform 方法

1. 最大最小归一化手动化与自动化代码对比演示 1：

公式：

$X_{std}=\frac{X_{}-X_{.}min(axis=0)}{X_{.}max(axis=0)-X_{.}min(axis=0)}$

$X_{scaled}=X_{std}\times (max-min)+min$ ，范围 $[0,1]$

代码演示：

#!/usr/bin/env python
# -*-coding:utf-8-*-
from sklearn.preprocessing import MinMaxScaler
import numpy as np

data = np.array([[4,2,3],
                [1,5,6]])

print("data格式: ",type(data))
# 手动归一化
feature_range = [0,1]  # 要映射的区间
print("每一列的最小值: ",data.min(axis=0))  # axis 坐标轴 0 ，从上往下，每一列的最小值
print("每一列的最大值: ",data.max(axis=0))  # axis 坐标轴 0 ，从上往下，每一列的最大值
x_std = (data-data.min(axis=0))/(data.max(axis=0)-data.min(axis=0))  # axis 坐标轴 0 ，从上往下，列 ，标准化
x_scaled = x_std*(feature_range[1]-feature_range[0]) + feature_range[0]
print('手动归一化结果：\n{}'.format(x_scaled))

# 自动归一化
scaler = MinMaxScaler()
print('自动归一化结果:\n{}'.format(scaler.fit_transform(data)))

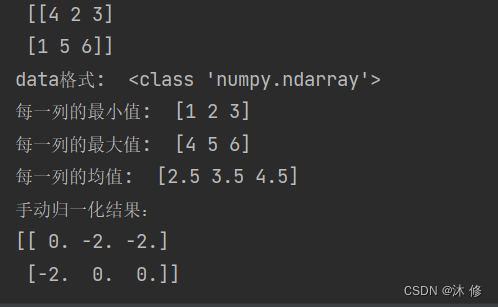
运行结果：

> 这里 [ 4 ]   算是一列，同理 [ 2 ] [ 3 ]  各自算一列
> 	  [ 1 ]				   [ 5 ] [ 6 ]

在第一列中，最小的是1，第二列最小的是 2，第三列最小的是3，所以 data.min(axis) 的值便是 [1, 2, 3 ]
同理可得 data.max(axis) 的值，得出每一列的最大值 [ 4, 5, 6 ]

2. 均值归一化手动化代码演示：

公式：

$X_{std}=\frac{X-X_{mean}}{X_{max}-X_{min}}$
$X_{scaled}=X_{std}\times (max-min)+min$ ，范围 $[-1,1]$

手动化代码演示 实例1：

#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np

data = np.array([[ 0, -3,  1],
              [ 3,  1,  2],
              [ 0,  1, -1]])
              
print("矩阵: \n",data)
print("data格式: ",type(data))
# 手动归一化
feature_range = [-1,1]  # 要映射的区间
print("每一列的最小值: ",data.min(axis=0))  # axis 坐标轴 0 ，从上往下，每一列的最小值
print("每一列的最大值: ",data.max(axis=0))  # axis 坐标轴 0 ，从上往下，每一列的最大值
print("每一列的均值: ",data.mean(axis=0))   # axis 坐标轴 0 ，从上往下，每一列的均值
x_std = (data-data.mean(axis=0))/(data.max(axis=0)-data.min(axis=0))  # axis 坐标轴 0 ，从上往下，列 ，标准化
x_scaled = x_std*(feature_range[1]-feature_range[0]) + feature_range[0]
print('手动归一化结果：\n{}'.format(x_scaled))

运行结果 1：

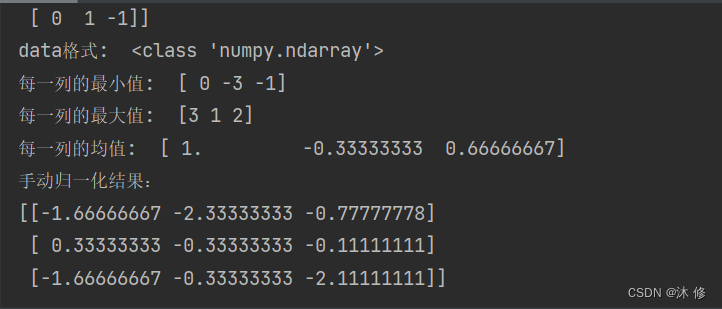
手动化代码演示 实例2：

#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np

data = np.array([[4,2,3],
                [1,5,6]])
              
print("矩阵: \n",data)
print("data格式: ",type(data))
# 手动归一化
feature_range = [-1,1]  # 要映射的区间
print("每一列的最小值: ",data.min(axis=0))  # axis 坐标轴 0 ，从上往下，每一列的最小值
print("每一列的最大值: ",data.max(axis=0))  # axis 坐标轴 0 ，从上往下，每一列的最大值
print("每一列的均值: ",data.mean(axis=0))   # axis 坐标轴 0 ，从上往下，每一列的均值
x_std = (data-data.mean(axis=0))/(data.max(axis=0)-data.min(axis=0))  # axis 坐标轴 0 ，从上往下，列 ，标准化
x_scaled = x_std*(feature_range[1]-feature_range[0]) + feature_range[0]
print('手动归一化结果：\n{}'.format(x_scaled))

运行结果 2：

3. 小数定标归一化手动化代码演示：

公式：

$X_{new}=\frac{X}{10^k}$

• k 取决于 $X$ 内的属性取值中的最大绝对值
• 小数定标规范化就是通过移动小数点的位置来进行规范化。
• 小数点移动多少位取决于 $X$ 内的属性的取值中的最大绝对值。

这里的 $X$ 内的属性代指样本实例的某种属性，比如长度、宽度、数量等。

手动化代码演示：

#!/usr/bin/env python
# -*-coding:utf-8-*-

from sklearn import preprocessing
import numpy as np

# 初始化数据
data = np.array([[ 0, -3,  1],
              [ 3,  1,  2],
              [ 0,  1, -1]])

# 小数定标规范化    # 手动归一化
j = np.ceil(np.log10(np.max(abs(data))))  # abs函数返回一个绝对值的矩阵
scaled_data = data/(10**j)  #幂函数运算
print(scaled_data)

abs()函数可以对矩阵内的所有数据进行绝对值处理，返回一个只有绝对值的矩阵，np.max() 方法则对绝对值矩阵进行一个最大值处理，找出矩阵内最大的一个值出来，而ceil()方法则是向上取整数，可不是四舍五入那种取整数的方法，而是直接去掉浮点数。
由此得到了以原始数据集内绝对值的最大值为基础的 k 值，利用公式算出了归一化后的新数据。

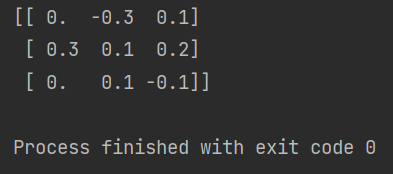
运行结果：

参考链接：
python abs是什么意思？abs函数有什么用处？

Python numpy.log10用法及代码示例

numpy_ceil函数

4. 零-均值标准化(均值移除)手动与自动化代码演示：

官方文档

sklearn.preprocessing.scale()函数

sklearn.preprocessing.scale(X, axis=0, with_mean=True, with_std=True, copy=True)

沿着某个轴(axis)标准化数据集，以均值为中心，以分量为单位方差
axis 的值可以是 0 或 1 ， 0 代表了从上往下，列，1代表了从左到右，行

参数	数据类型	意义
X	{array-like, sparse matrix}	以此数据为中心缩放
axis	int (0 by default)	沿着计算均值和标准差的轴。如果是0，独立的标准化每个特征，如果是1则标准化每个样本（即行）
with_mean	boolean, True by default	如果是True，缩放之前先中心化数据
with_std	boolean, True by default	如果是True，以单位方差法缩放数据（或者等价地，单位标准差）
copy	boolean, optional, default True	False：原地执行行标准化并避免复制（如果输入已经是一个numpy数组或者scipy.sparse CSC矩阵以及axis是1 —— 行复制）

公式：

$X_{new}=\frac{X-X_{mean}}{X_{std}}$ ，均值为 0，方差为 1

手动化与自动化代码对比演示：

#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np
from sklearn import preprocessing

data = np.array([[ 0, -3,  1],
              [ 3,  1,  2],
              [ 0,  1, -1]])
print("矩阵: \n",data)
print("data格式: ",type(data))
# 手动归一化
feature_range = [0,1]  # 要映射的区间
print("每一列的均值: ",data.mean(axis=0))   # axis 坐标轴 0 ，从上往下，每一列的均值
print("每一列的方差: ",data.std(axis=0))   # axis 坐标轴 0 ，从上往下，每一列的均值
x_std = (data-data.mean(axis=0))/(data.std(axis=0))  # axis 坐标轴 0 ，从上往下，列 ，标准化

print('手动标准化结果：\n{}'.format(x_std))

data = np.array([[ 0, -3,  1],
              [ 3,  1,  2],
              [ 0,  1, -1]])

# 将数据进行Z-Score规范化   自动标准化
scaled_data = preprocessing.scale(data)
print("自动标准化结果: \n",scaled_data)

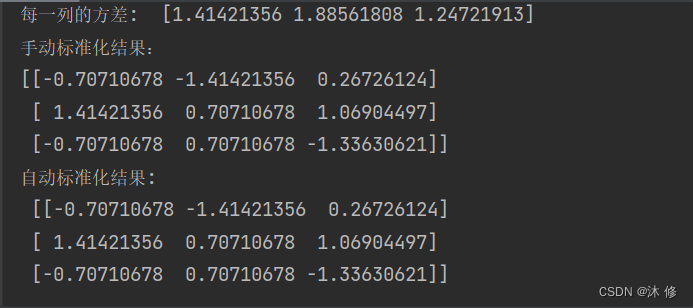
运行结果：

fit、transform 是什么？

1. MinMaxScaler 归一化接口的 fit 拟合函数

MinMaxScaler 的 fit 函数的官方定义：

Compute the minimum and maximum to be used for later scaling.
翻译一下：计算用于进行特征缩放的最大值、最小值

也就是说，通过 fit 函数可以先对需要归一化的数据集进行最大、最小值的计算，至于说最终归一化的结果是多少，对不起，fit 函数到此为止了。

fit n. 拟合

从这里可以知道其实 fit，拟合函数 fit 只能做到将最有价值的最大、最小值，从数据集中提取出来，然后就无法进行下一步的操作 —— 归一化 或 标准化，还有这里提到的仅仅是 MinMaxScaler 模块，这是最大最小归一化模块，要区分下一个要介绍的 StandardScaler 标准化接口的 fit 拟合函数

MinMaxScaler 的 fit 拟合函数代码演示：

#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np
from sklearn.preprocessing import MinMaxScaler

# 创建数组
data_rn = np.random.randint(-10, 10, 10).reshape(5, 2)  # np模块在-10 到 10 的范围内随机抽取10 个数，并且组成 5行 2 列的矩阵
print("矩阵: \n",data_rn)
# 进行归一化
scaler_mmc = MinMaxScaler()
scaler_mmc_fit = scaler_mmc.fit(data_rn)   # 默认 axix=0 按列处理，也就是处理向量
print("提取矩阵中的最大值: ",scaler_mmc_fit.data_max_)  # 最大值
print("提取矩阵中的最小值: ",scaler_mmc_fit.data_min_)  # 最小值
print("提取矩阵中的极差值: ",scaler_mmc_fit.data_range_) # 极差 最大值减最小值，有两列最大最小值，那么就会有两个极差

运行结果：

这是提取每一列的最大值和最小值，第一列最大值是5，第二列最大值是3，第一列最小值是-8，第二列最小值是-4。

2. StandardScaler 标准化接口的 fit 拟合函数

StandardScaler 的 fit 函数的官方定义：

Compute the mean and std to be used for later scaling
翻译一下：计算用于进行特征缩放的均值、标准差
使用StandardScaler 模块的 fit 拟合函数可以对需要标准化的数据集进行均值、标准差的计算
.

StandardScaler 的 fit 拟合函数代码演示：

#!/usr/bin/env python
# -*-coding:utf-8-*-
import numpy as np
from sklearn.preprocessing import StandardScaler

# 创建数组
data_rn = np.random.randint(-10, 10, 10).reshape(5, 2)  # np模块在-10 到 10 的范围内随机抽取10 个数，并且组成 5行 2 列的矩阵
print("矩阵: \n",data_rn)
# 进行标准化
scaler_ss = StandardScaler()
scaler_ss_fit = scaler_ss.fit(data_rn)
print("均值: ",scaler_ss_fit.mean_) # 均值，默认对列获取均值
print("方差: ",scaler_ss_fit.var_) # 方差，默认对列获取方差

运行结果：

可以看出均值和方差都是对每一列进行提取，然后均值和方差都各自得到了两个有价值的均值和方差，所以 fit 拟合函数的存在意义便是如此，从数据中提取有价值的数据出来，为后面的其他数据预处理操作，做准备。

总结一下 fit 的用法：
简单来说，就是求得数据集的均值、方差、最大值、最小值等固有的属性，经常和 transform 搭配使用

从算法模型的角度上讲，fit 拟合过程可以理解为一个训练过程。

transform 与 fit_transform 函数的理解

官方文档的定义：

MinMaxScaler：Scale features of X according to feature_range.
StandardScaler：Perform standardization by centering and scaling

翻译一下：

MinMaxScaler：根据 feature_range 进行 $X$ 的缩放
StandardScaler：通过居中和缩放执行标准化
也就是说，其实 transform 才是真正做归一化和标准化的函数，fit 拟合函数只是做了前面的准备工作。

从算法模型的角度上讲，transform 过程可以理解为一个转换过程。
用法也很简单，对前面 fit 过的数据集直接进行操作即可

# 归一化
scaler_mmc = MinMaxScaler()
scaler_mmc_fit = scaler_mmc.fit(data_rn)   # 默认 axix=0 按列处理，也就是处理向量
scaler_mmc_result = scaler_mmc.transform(data_rn)
# 标准化
scaler_ss = StandardScaler()
scaler_ss_fit = scaler_ss.fit(data_rn)
scaler_ss_result = scaler_ss.transform(data_rn)  

最终的结果和直接进行 fit_transform 的结果一致。即：

fit + transform = fit_transform

即 fit_transform 是 fit 和 transform 的组合，整个过程既包括了训练又包含了转换 fit_transform
对数据先拟合 fit，找到数据的整体指标，如均值、方差、最大值最小值等，然后对数据集进行转换transform，从而实现数据的标准化、归一化操作。

项目中使用技巧 —— fit_transform 和 transform

了解了 fit、transform 的用法之后，可以再来学习下在项目中使用的小技巧。

项目的数据集一般都会分为 训练集和测试集，训练集用来训练模型，测试集用来验证模型效果。

要想训练的模型在测试集上也能取得很好的得分，不但需要保证训练集数据和测试集数据分布相同，还必须保证对它们进行同样的数据预处理操作。比如：标准化和归一化。

所以一般对于数据集处理上，会直接对训练集进行 拟合+转换，然后直接对测试集 进行转换。

注意了，是用训练集进行拟合，然后对训练集、测试集都用拟合好的”模型“进行转换，一定要明白这个逻辑！！

MinMaxScaler 接口代码演示：

from sklearn.preprocessing import MinMaxScaler 

scaler_mmc = MinMaxScaler()
# 训练集操作
new_train_x = scaler_mmc.fit_transform(train_x)
# 测试集操作
new_test_x = scaler_mmc.tranform(test_x)

StandardScaler 接口代码演示：

from sklearn.preprocessing import StandardScaler

scaler_ss = StandardScaler()
# 训练集操作
new_train_x = scaler_ss.fit_transform(train_x)
# 测试集操作
new_test_x = scaler_ss.tranform(test_x)

一定要注意，一定要注意，一定要注意：
不能对训练集和测试集都使用 fit_transform，虽然这样对测试集也能正常转换（归一化或标准化），但是两个结果不是在同一个标准下的，具有明显差异。

总结：

1. 在用机器学习解决问题时，会将数据集划分成训练集和测试集；
2. 我们可以先用fit_transform()方法处理训练集，再用transform()方法处理测试集。这时，在归一化测试集时，使用的是训练集的统计量，这么做是为了让训练集和测试集更相似。使算法在两者上的表现尽可能相同(这里意味着使用了fit_transform()方法后，相当于使用了 fit() 方法，然后在使用transform() 方法，也就不需要 fit() 了，因为 fit_transform() 方法已经将训练集的 fit() 后的数据，都存储了下来，供 transform() 方法使用)；
3. 若对测试集使用了fit_transform()方法，则会用测试集自己的统计量来归一化数据。在测试集上千万不要混用这两个方法，如果在测试集上使用了fit_transform()方法，会导致在测试集上的损失一直比验证集上的大很多；
4. 还有一个fit()方法没说，这个是最简单的，它和fit_transform()是相同的，只不过后者会返回转换后的结果，而前者是不会返回的，只会训练转换器；
5. 首先，如果要想在 fit_transform 的过程中查看数据的分布，可以通过分解动作先 fit 再 transform，fit 后的结果就包含了数据的分布情况；
6. 如果不关心数据分布只关心最终的结果可以直接使用 fit_transform 一步到位；
7. 其次，在项目上对训练数据和测试数据需要使用同样的标准进行转换，切记不可分别进行 fit_transform。

参考链接：

做数据处理，你连 fit、transform、fit_transform 都分不清？

对sklearn中transform()和fit_transform()的深入理解

python numpy实现 标准差，方差

【机器学习】数据归一化——MinMaxScaler理解

二、normalize() 方法

normalize 方法的参数：

sklearn.preprocessing.normalize(X, norm='l2', *, axis=1, copy=True, return_norm=False)

$X$: 要规范化的数据
$norm$：{‘l1’, ‘l2’, ‘max’}，指定范数，默认是矩阵的 2 - 范数，即 l2，但通常而言，常用矩阵的 1- 范数，即 l1 范数，l1归一化：将每个数据除以l1范数(所有数据列的绝对值之和的最大值)
max是矩阵的无穷范数、$||A|{|}_{\propto }$

这个方法经常用于确保数据点没有因为特征的基本性质而产生较大的差异，即确保数据处于同一数量级，提高不同特征数据的可比性。

$axis$：轴，默认是 axis = 1 ， 即按样本的行进行计算，用于规范化数据的轴。如果为 1，则独立地对每个样本进行归一化，否则（如果为 0）对每个特征进行归一化，即特征向量。

$copy$：bool, default=True

总思路参考链接：

scikit-learn初级