1.任务描述
本关任务:
- 了解有信息搜索策略的算法思想;
- 能够运用计算机语言实现搜索算法;
- 应用
A*搜索算法解决罗马尼亚问题;
2.相关知识
A*搜索
- 算法介绍
A*算法常用于 二维地图路径规划,算法所采用的启发式搜索可以利用实际问题所具备的启发式信息来指导搜索,从而减少搜索范围,控制搜索规模,降低实际问题的复杂度。
- 算法原理:
A*算法的原理是设计一个代价估计函数:其中 **评估函数F(n)**是从起始节点通过节点n的到达目标节点的最小代价路径的估计值,函数G(n)是从起始节点到n节点的已走过路径的实际代价,函数H(n)是从n节点到目标节点可能的最优路径的估计代价 。
函数 H(n)表明了算法使用的启发信息,它来源于人们对路径规划问题的认识,依赖某种经验估计。根据 F(n)可以计算出当前节点的代价,并可以对下一次能够到达的节点进行评估。
采用每次搜索都找到代价值最小的点再继续往外搜索的过程,一步一步找到最优路径。
3.编程要求
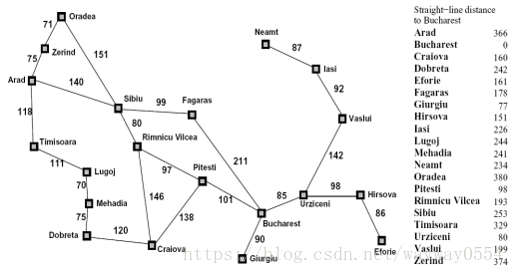
罗马尼亚问题:agent在罗马尼亚度假,目前位于 Arad 城市。agent明天有航班从Bucharest 起飞,不能改签退票。
现在你需要寻找到 Bucharest 的最短路径,在右侧编辑器补充void A_star(int goal,node &src,Graph &graph)函数,使用编写的搜索算法代码求解罗马尼亚问题:
4.测试说明
平台会对你编写的代码进行测试:
预期输出:
solution: 0-> 15-> 14-> 13-> 1-> end
cost:418
5.实验过程
下面是关于非补充部分的代码解释:
1.宏定义每个城市名和编号
#define A 0
#define B 1
#define C 2
#define D 3
#define E 4
#define F 5
#define G 6
#define H 7
#define I 8
#define L 9
#define M 10
#define N 11
#define O 12
#define P 13
#define R 14
#define S 15
#define T 16
#define U 17
#define V 18
#define Z 19
2.记录启发函数h数组,即从n节点到目标节点可能的最优路径的估计代价
int h[20] =//从n节点到目标节点可能的最优路径的估计代价
{ 366,0,160,242,161,
178,77,151,226,244,
241,234,380,98,193,
253,329,80,199,374 };
3.定义城市节点的结构体
struct node
{
int g; //从起始节点到n节点的已走过路径的实际代价
int h; //从n节点到目标节点可能的最优路径的估计代价
int f; //代价估计函数
int name;
node(int name, int g, int h) { //构造函数
this->name = name;
this->g = g;
this->h = h;
this->f = g + h;
};
//重载运算符
bool operator <(const node& a)const { return f < a.f; }
};
4.定义图结构,记录图中各节点和边的信息
class Graph //图结构
{
public:
Graph() {
memset(graph, -1, sizeof(graph)); //图初始化为-1,代表无边
}
int getEdge(int from, int to) { //获取边的开销
return graph[from][to];
}
void addEdge(int from, int to, int cost) { //新增一条边及其开销
if (from >= 20 || from < 0 || to >= 20 || to < 0)
return;
graph[from][to] = cost;
}
void init() { //图初始化
addEdge(O, Z, 71);
addEdge(Z, O, 71);
addEdge(O, S, 151);
addEdge(S, O, 151);
addEdge(Z, A, 75);
addEdge(A, Z, 75);
addEdge(A, S, 140);
addEdge(S, A, 140);
addEdge(A, T, 118);
addEdge(T, A, 118);
addEdge(T, L, 111);
addEdge(L, T, 111);
addEdge(L, M, 70);
addEdge(M, L, 70);
addEdge(M, D, 75);
addEdge(D, M, 75);
addEdge(D, C, 120);
addEdge(C, D, 120);
addEdge(C, R, 146);
addEdge(R, C, 146);
addEdge(S, R, 80);
addEdge(R, S, 80);
addEdge(S, F, 99);
addEdge(F, S, 99);
addEdge(F, B, 211);
addEdge(B, F, 211);
addEdge(P, C, 138);
addEdge(C, P, 138);
addEdge(R, P, 97);
addEdge(P, R, 97);
addEdge(P, B, 101);
addEdge(B, P, 101);
addEdge(B, G, 90);
addEdge(G, B, 90);
addEdge(B, U, 85);
addEdge(U, B, 85);
addEdge(U, H, 98);
addEdge(H, U, 98);
addEdge(H, E, 86);
addEdge(E, H, 86);
addEdge(U, V, 142);
addEdge(V, U, 142);
addEdge(I, V, 92);
addEdge(V, I, 92);
addEdge(I, N, 87);
addEdge(N, I, 87);
}
private:
int graph[20][20]; //图数组,用来保存图信息,最多有20个节点
};
5.一些数据结构的定义
bool list[20]; //用于记录节点i是否在openList集合中
vector<node> openList; //扩展节点集合
bool closeList[20]; //已访问节点集合
stack<int> road; //路径
int parent[20]; //父节点,用于回溯构造路径
1.补充void A_star(int goal, node& src, Graph& graph)函数
主要思想是利用一个估价函数f(n)来评估每个节点n的优先级,f(n)由两部分组成:g(n)表示从起点到节点n的实际代价,h(n)表示从节点n到终点的预估代价。A*算法每次选择f(n)最小的节点进行扩展,直到找到终点或者没有可扩展的节点为止
代码如下:
void A_star(int goal, node& src, Graph& graph)//A*搜索算法
{
openList.push_back(src); //扩展集合加入起始节点
sort(openList.begin(), openList.end()); //排序扩展集合的节点,以取出代价最小的节点
while (!openList.empty())
{
/********** Begin **********/
node curNode = openList[0]; //取出扩展集合第一个节点,即代价最小的节点
if (curNode.name == goal) { //如果当前节点就是目标节点,则退出
return;
}
openList.erase(openList.begin()); //将当前节点从扩展列表中删除
closeList[curNode.name] = true; //将当前节点加入已访问节点
list[curNode.name] = false; //标记当前节点已不在扩展集合中
for (int i = 0; i < 20; i++) { //开始扩展当前节点,即找到其邻居节点
if (graph.getEdge(i, curNode.name) == -1) { //若不是当前节点的邻居节点,跳到下一个节点
continue;
}
if (closeList[i]) { //若此节点已加入已访问集合closeList,也跳到下一个节点
continue;
}
int g1 = curNode.g + graph.getEdge(i, curNode.name); //计算起始节点到当前节点i的g值
int h1 = h[i]; //获得当前节点i的h值
if (list[i]) { //如果节点i在openList中
for (int j = 0; j < openList.size(); j++) {
if (i == openList[j].name) { //首先找到节点i的位置,即j
if (g1 < openList[j].g) { //如果新的路径的花销更小,则更新
openList[j].g = g1;
openList[j].f = g1 + openList[j].h;
parent[i] = curNode.name; //记录父节点
break;
}
}
}
}
else { //如果节点i不在openList,则将其加入其中(因为扩展时访问了它)
node newNode(i, g1, h1); //创建新节点,其参数已知
openList.push_back(newNode); //新节点加入openList中
parent[i] = curNode.name; //记录父节点
list[i] = true; //记录节点i加入了openList
}
}
sort(openList.begin(), openList.end()); //扩展完当前节点后要对openList重新排序
/********** End **********/
}
}
首先扩展起始节点,将扩展集合中的节点按照优先级进行排序。接着按照优先级不断扩展扩展集合中的节点,直到找到终点或者没有可扩展的节点为止。
每次扩展首先取出扩展集合第一个节点,判断其是否为目标节点,若是则退出。扩展该节点后需要将其加入已访问集合,并从扩展集合中删除,同时用list数组标记其已扩展。
接着扩展该节点,即寻找其邻居节点。
如果邻居节点在扩展集合中,则查看其更新后代价是否比原本的代价更优,优则更新它。同时记录父节点以用于回溯生成路径
如果邻居节点不在扩展集合中,则将其加入扩展集合中,记录父节点,并用list数组标记为在扩展集合中
每次扩展完节点后都要对扩展集合里的节点进行一次优先级的排序,用于下一个循环来取出当前优先级最高的节点
6.void print_result(Graph& graph)函数
用于打印路径和开销
void print_result(Graph& graph) //用于打印路径和开销
{
int p = openList[0].name; //p即为目标节点
int lastNodeNum;
road.push(p); //目标节点压入栈中,之后最后才输出
while (parent[p] != -1) //不断回溯获得一条完整路径
{
road.push(parent[p]);
p = parent[p];
}
lastNodeNum = road.top(); //起始节点
int cost = 0; //总开销
cout << "solution: ";
while (!road.empty()) //栈不为空就继续循环
{
cout << road.top() << "-> ";
if (road.top() != lastNodeNum) //如果栈顶元素不是终点
{
cost += graph.getEdge(lastNodeNum, road.top()); //添加花销
lastNodeNum = road.top(); //更新栈顶元素
}
road.pop(); //弹出栈顶元素
}
cout << "end" << endl;
cout << "cost:" << cost;
}
6.完整代码
#include<iostream>
#include<vector>
#include<memory.h>
#include<stack>
#include<algorithm>
#define A 0
#define B 1
#define C 2
#define D 3
#define E 4
#define F 5
#define G 6
#define H 7
#define I 8
#define L 9
#define M 10
#define N 11
#define O 12
#define P 13
#define R 14
#define S 15
#define T 16
#define U 17
#define V 18
#define Z 19
using namespace std;
int h[20] =//从n节点到目标节点可能的最优路径的估计代价
{ 366,0,160,242,161,
178,77,151,226,244,
241,234,380,98,193,
253,329,80,199,374 };
/*
*一个节点结构,node
*/
struct node
{
int g; //从起始节点到n节点的已走过路径的实际代价
int h; //从n节点到目标节点可能的最优路径的估计代价
int f; //代价估计函数
int name;
node(int name, int g, int h) { //构造函数
this->name = name;
this->g = g;
this->h = h;
this->f = g + h;
};
//重载运算符
bool operator <(const node& a)const { return f < a.f; }
};
class Graph //图结构
{
public:
Graph() {
memset(graph, -1, sizeof(graph)); //图初始化为-1,代表无边
}
int getEdge(int from, int to) { //获取边的开销
return graph[from][to];
}
void addEdge(int from, int to, int cost) { //新增一条边及其开销
if (from >= 20 || from < 0 || to >= 20 || to < 0)
return;
graph[from][to] = cost;
}
void init() { //图初始化
addEdge(O, Z, 71);
addEdge(Z, O, 71);
addEdge(O, S, 151);
addEdge(S, O, 151);
addEdge(Z, A, 75);
addEdge(A, Z, 75);
addEdge(A, S, 140);
addEdge(S, A, 140);
addEdge(A, T, 118);
addEdge(T, A, 118);
addEdge(T, L, 111);
addEdge(L, T, 111);
addEdge(L, M, 70);
addEdge(M, L, 70);
addEdge(M, D, 75);
addEdge(D, M, 75);
addEdge(D, C, 120);
addEdge(C, D, 120);
addEdge(C, R, 146);
addEdge(R, C, 146);
addEdge(S, R, 80);
addEdge(R, S, 80);
addEdge(S, F, 99);
addEdge(F, S, 99);
addEdge(F, B, 211);
addEdge(B, F, 211);
addEdge(P, C, 138);
addEdge(C, P, 138);
addEdge(R, P, 97);
addEdge(P, R, 97);
addEdge(P, B, 101);
addEdge(B, P, 101);
addEdge(B, G, 90);
addEdge(G, B, 90);
addEdge(B, U, 85);
addEdge(U, B, 85);
addEdge(U, H, 98);
addEdge(H, U, 98);
addEdge(H, E, 86);
addEdge(E, H, 86);
addEdge(U, V, 142);
addEdge(V, U, 142);
addEdge(I, V, 92);
addEdge(V, I, 92);
addEdge(I, N, 87);
addEdge(N, I, 87);
}
private:
int graph[20][20]; //图数组,用来保存图信息,最多有20个节点
};
bool list[20]; //用于记录节点i是否在openList集合中
vector<node> openList; //扩展节点集合
bool closeList[20]; //已访问节点集合
stack<int> road; //路径
int parent[20]; //父节点,用于回溯构造路径
void A_star(int goal, node& src, Graph& graph)//A*搜索算法
{
openList.push_back(src); //扩展集合加入起始节点
sort(openList.begin(), openList.end()); //排序扩展集合的节点,以取出代价最小的节点
while (!openList.empty())
{
/********** Begin **********/
node curNode = openList[0]; //取出扩展集合第一个节点,即代价最小的节点
if (curNode.name == goal) { //如果当前节点就是目标节点,则退出
return;
}
openList.erase(openList.begin()); //将当前节点从扩展列表中删除
closeList[curNode.name] = true; //将当前节点加入已访问节点
list[curNode.name] = false; //标记当前节点已不在扩展集合中
for (int i = 0; i < 20; i++) { //开始扩展当前节点,即找到其邻居节点
if (graph.getEdge(i, curNode.name) == -1) { //若不是当前节点的邻居节点,跳到下一个节点
continue;
}
if (closeList[i]) { //若此节点已加入已访问集合closeList,也跳到下一个节点
continue;
}
int g1 = curNode.g + graph.getEdge(i, curNode.name); //计算起始节点到当前节点i的g值
int h1 = h[i]; //获得当前节点i的h值
if (list[i]) { //如果节点i在openList中
for (int j = 0; j < openList.size(); j++) {
if (i == openList[j].name) { //首先找到节点i的位置,即j
if (g1 < openList[j].g) { //如果新的路径的花销更小,则更新
openList[j].g = g1;
openList[j].f = g1 + openList[j].h;
parent[i] = curNode.name; //记录父节点
break;
}
}
}
}
else { //如果节点i不在openList,则将其加入其中(因为扩展时访问了它)
node newNode(i, g1, h1); //创建新节点,其参数已知
openList.push_back(newNode); //新节点加入openList中
parent[i] = curNode.name; //记录父节点
list[i] = true; //记录节点i加入了openList
}
}
sort(openList.begin(), openList.end()); //扩展完当前节点后要对openList重新排序
/********** End **********/
}
}
void print_result(Graph& graph) //用于打印路径和开销
{
int p = openList[0].name; //p即为目标节点
int lastNodeNum;
road.push(p); //目标节点压入栈中,之后最后才输出
while (parent[p] != -1) //不断回溯获得一条完整路径
{
road.push(parent[p]);
p = parent[p];
}
lastNodeNum = road.top(); //起始节点
int cost = 0; //总开销
cout << "solution: ";
while (!road.empty()) //栈不为空就继续循环
{
cout << road.top() << "-> ";
if (road.top() != lastNodeNum) //如果栈顶元素不是终点
{
cost += graph.getEdge(lastNodeNum, road.top()); //添加花销
lastNodeNum = road.top(); //更新栈顶元素
}
road.pop(); //弹出栈顶元素
}
cout << "end" << endl;
cout << "cost:" << cost;
}
int main()
{
Graph graph;
graph.init();
int goal = B; //目标节点B
node src(A, 0, h[A]); //起始节点A
list[A] = true;
memset(parent, -1, sizeof(parent)); //初始化parent
memset(list, false, sizeof(list)); //初始化list
A_star(goal, src, graph);
print_result(graph);
return 0;
}
运行结果:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ukaYZTHr-1678452048946)(C:\Users\86159\AppData\Roaming\Typora\typora-user-images\1678451967482.png)]](https://img-blog.csdnimg.cn/e733b49ffd4b40f4822b78a1c69c29f9.png)