最小路径和
中等
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
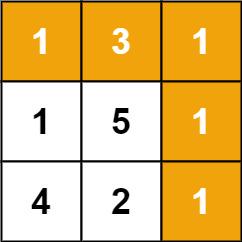
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
题解
我们可以复制一个大小相同的二维数组,初始化(0,0)
我们可以知道每次只能往右往下走,且求最小路径
我们可以先求出第一列和第一行的值,从1开始,每个值都是前一个值加上当前值
例如第一列dp[0][0]=grid[0][0]=1
dp[0][1] = dp[0][0] + grid[1][0] = 2
dp[0][2] = dp[1][0] + grid[2][0] = 6
初始化完第一列第一行后,我们可以知道从(1,1)开始每个值都是左边一个和上边一个的最小值加上当前位置的值就是这条路径的最小值,我们可以先用两个变量获取这两个值,在取小的那个数赋给dp[i][j]

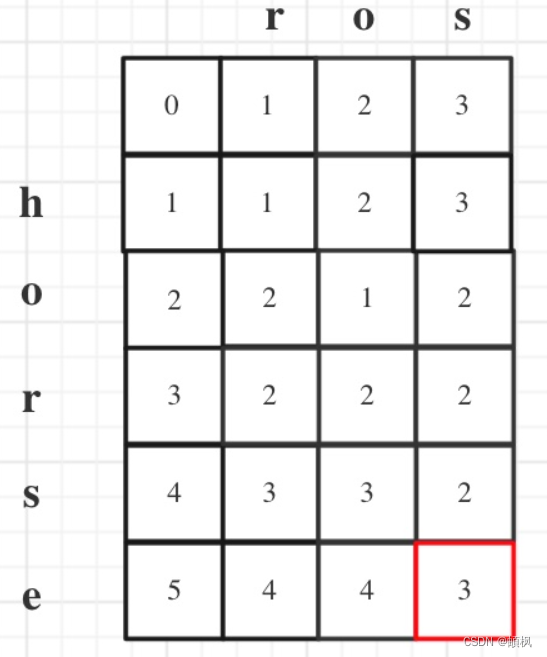
1 | 1+3=4 | 1+3+1=5 |
1+1=2 | 1+1+5=7 | 1+3+1+1=6 |
1+1+4=6 | 1+1+4+2=8 | 1+3+1+1+1=7 |
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int dp[][] = new int[m][n];
dp[0][0] = grid[0][0];
for(int i = 1;i < m;i++){
dp[i][0] = dp[i-1][0] + grid[i][0];
}
for(int j = 1;j < n;j++){
dp[0][j] = dp[0][j-1] + grid[0][j];
}
for(int i = 1;i < m;i++){
for(int j = 1;j < n;j++){
int r = dp[i-1][j] + grid[i][j];
int c = dp[i][j-1] + grid[i][j];
dp[i][j] = Math.min(r,c);
System.out.println(dp[i][j]);
}
}
return dp[m-1][n-1];
}
}