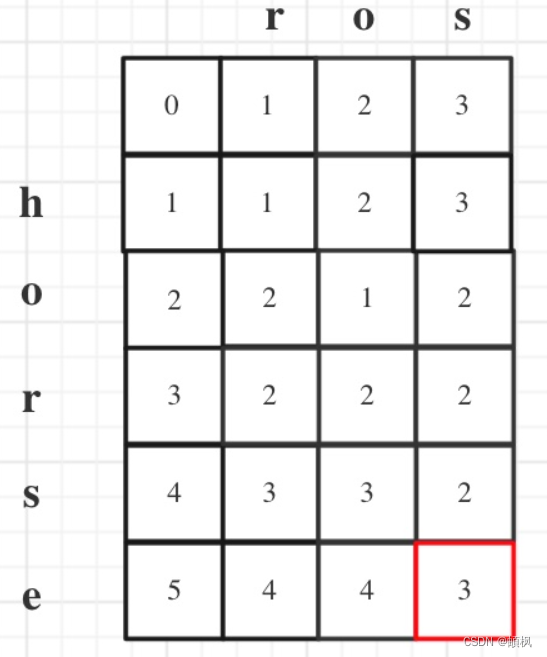
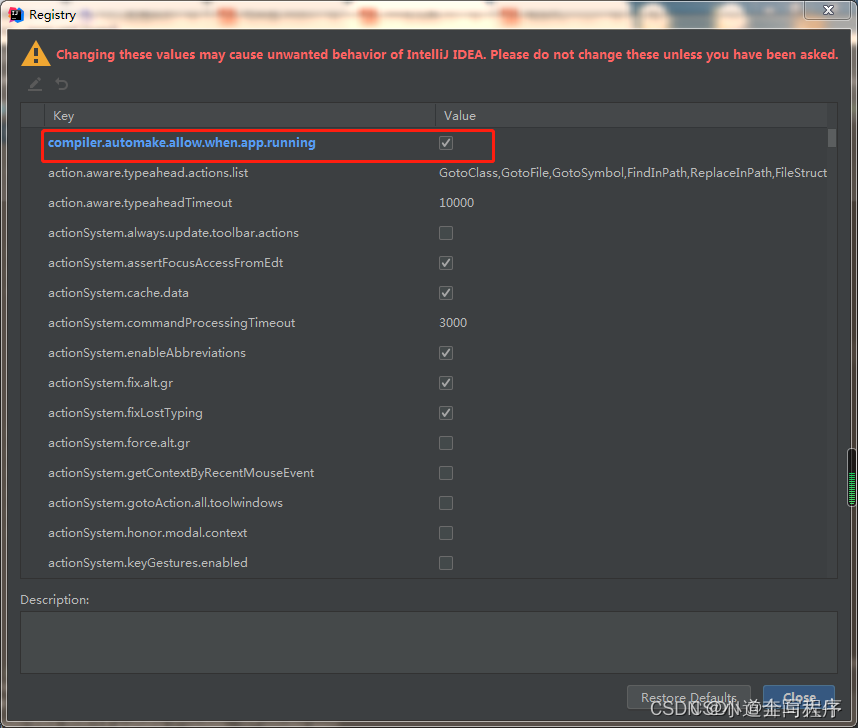
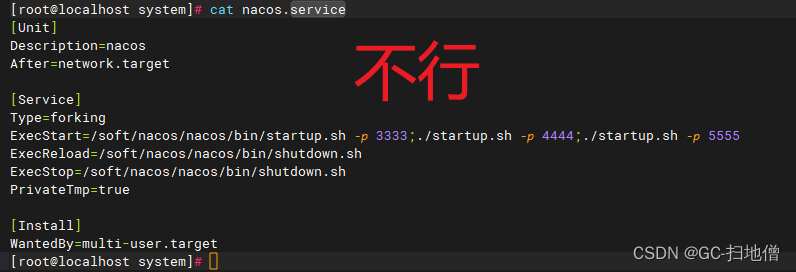
离散型
设随机变量(X,Y)的联合分布律为
| X\Y | 0 | 1 |
|---|---|---|
| 0 | 0.1 | 0.2 |
| 1 | 0.3 | 0.4 |
(1)求E(X)
先求x的边缘分布律,表格里x=0的概率为0.1+0.2,于是我们可得
| X | 0 | 1 |
|---|---|---|
| P | 0.3 | 0.7 |
直接求E(X)即可,得到结果
(2)求E(XY)
直接x与y相乘就行。
记得别乘多了,别的算了又算遍
。
(3)求E(X+Y)
和上面一样,x与y相加就行。
连续型
已知随机变量(X,Y)的概率密度。
(1)求E(X)
和求一维连续型随机变量的步骤差不多。把E(X)的x当作g(x),然后求个这个二重积分即可。
由于函数在除了[0,1]的区间上都为0,对其积分也为0。同时x和y的上下限都已经给出。我们可以得到。
关于二重积分的相关知识在高数下。这里作简述:这里的二重积分是化成了x型。也就是把dx往前提;然后先写x的取值范围再写y的取值范围。由于x是自变量所以上下限应与y无关。所以这里是[0,1]而不是[y,1]。而y是因变量,所以上下限为[0,x]。所要求的式子与dy放在一起。然后就变成了求解定积分--先求对y的积分,再对得出来的结果求x的积分。
运算过程太多,这里写关键的。即
(2)求E(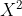 )
)
求步骤和上面一样,只不是是g(x)=
,所以式子变成了
上下限没变,计算方法没变。这里就直接放结果为
(3)求E(XY)
还是和上面一样的,式子变成了,结果为