从参数数量视角理解深度学习神经网络算法 DNN, CNN, RNN, LSTM 以python为工具

---

      ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ

1. 神经网络数据预处理

使用python写神经网络算法前，通常需要先对数据进行预处理，使得数据称为符合算法要求的形式。这不限于归一化和特征提取。特征和标签的形式常常是初学者容易糊涂的。
常见的情况可以分为两种，一种是常规的预测场景，另一种则是文本预测场景。
 

---

1.1 常规预测情景

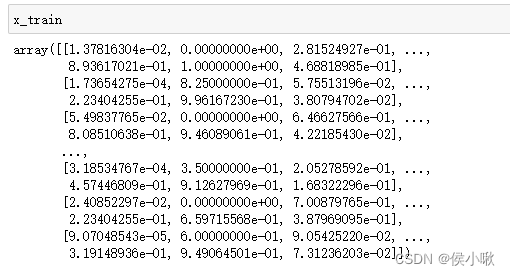
在常规的预测场景下，输入数据的shape可以分为三维情景和二维情景。
 
若为三维情景，输入数据的shape为(a,b,c)，其中c>1。即表示，共有a条样本，b个特征。每个特征的特征值的维度为c。（其中c=1时效果等同于二维情景，但设定方式有一定区别）
API中对应的参数:
input_shape=(c,b)
input_length=b
input_dim=c
 
若为二维情景，设输入数据的shape是(a,b)，则input_shape=(b,)
二维情景下的input_shape=(b,)相当于三维情境下的input_shape=(1,b)。
           
 
对于输出层，无论是分类问题还是回归问题，根据输出值个数，即每个标签值的维度来设定输出层神经元的数量。
如，对于对每个样本只输出一个一个数值的回归问题，则输出层只需要一个神经元，对于每个样本输出两个或多个回归值的问题，则在输出层可以设置多个神经元，每个神经元对应其中一个预测的输出。
对于分类问题，在输出层设定一个神经元即可以实现一般的二分类问题；对于二个类别以上的分类问题，则可以先对输入的数据进行预处理：假设有[0,1,2]三类，0类则可以改写为[1,0,0]，1类则则可以改写为[0,1,0]，2类则可以改写为[0,0,1]。然后在输出层设置3个神经元，每个神经元则负责输出一个数字，输出的3个数字组成一个形如[x1,x2,x3]的长度为3的一维数组。其中x1是预测出的该样本标签为0类的概率，x2是预测出的该样本标签为1类的概率，x3是预测出的该样本标签为2的概率。得到预测结果后，[x1,x2,x3]其中最大的数字对应的索引，即为预测出该样本可能的类别。需要进一步去转换。

---

1.2 文本预测场景

对于文本预测场景，则在数据预处理阶段有着一套相对成熟的编码思路。
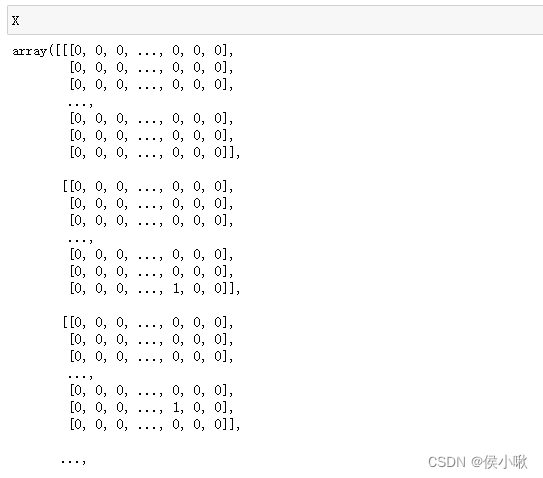
文本预测场景的数据形式通常都是三维形式，一般不再有二维形式。输入数据的shape为(a,b,c)，则表示a条样本数据，使用前b个字符，预测下一个或多个字符。c则等于训练样本中所有可能的种类的数量。
将每个特征的特征值都转化为形如：[0 0 … 0 1 0 0 … 0 ]的矩阵形式。其中该矩阵的每个位置，都表示一个字符，0表示否，1表示是该字符。该矩阵长度则为c。
相应的，标签数据也需要转化为这种形式。若只预测后边一个数据，则设置c个神经元，其余逻辑同上述多维情景。

    

---

2.全连接神经网络 DNN

对全连接神经网络，
首先以一个简单的神经网络结构为例：一个中间层，一个输出层。中间层设定5个神经元，输出层设定1个神经元。
 

全连接神经网络的每层参数的数量可以总结为，该层输入特征数据的数量（input_length）乘以该层神经元的数量，再加上该层神经元的数量。

代码示例如下

from keras.models import Sequential
from keras.layers import Dense

model1 = Sequential()
# 中间层 （或 隐藏层）
# 使用Dense()方法直接写第一个隐藏层，而不用写输入层时，要设定input_shape参数
model1.add(Dense(units = 5,   
                input_shape=(10,)     
                )  
           )  
# 输出层 1个神经元
model1.add(Dense(1))
model1.summary()

        
其中中间层有55个参数，即输入的10个特征，乘以5个神经元的数量，加上5个神经元对应着5个偏置参数。10×5+5=55。
5个神经元有5个输出值，即下一个Dense，即输出层的输入维度为5，而输出层神经元数量为1，且也对应着一个偏置，所以输出层的参数数量为5×1+1=6个。两个层一共有61个参数。
 
模型图示如下：

from keras.utils import plot_model  
plot_model(model1, show_shapes=True)  

            

---

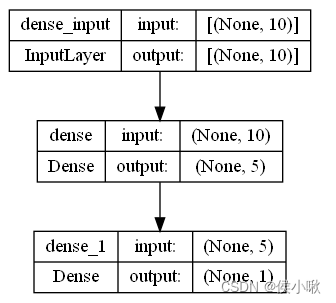
如果输入的是三维数据，(n,10,3)为例，则在传入参数时，一定要注意，input_shape=(3,10)，而不能写成(10,3)。
 
参数的个数与输入数据的维度input_dim无关（上边的数字3）。

model2 = Sequential()
model2.add(Dense(units = 5,   
                input_shape=(3,10)     
                )  
           )  


model2.add(Dense(1))
model2.summary()

输出结果：
          

from keras.utils import plot_model  
plot_model(model2, show_shapes=True)     

模型图示如下：
            
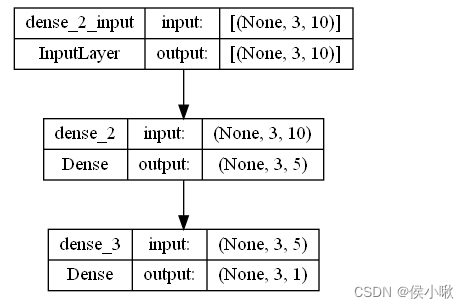
输入数据的是二维数据或三维数据，并不影响参数个数。

---

3.卷积神经网络CNN

这里建议选择使用Conv2D接口。(相对的是Conv1D)
 
设定卷积层神经元个数为32，即卷积层输出32个特征映射。
滤波核大小设定为3×3，输入数据的shape为(50,50,3)，可以理解为高50像素，宽50像素，且有3个色彩通道的图片，也可以理解为，每个样本初始数据有50×50个特征，每个特征的特征值shape为(3,)。
 
池化层使用2维最大池化。
 
输出层只设定一个神经元。
 
则卷积层的参数个数 = （卷积核长×卷积核宽×色彩通道数量+1）× 卷积层神经元个数
其中1指的是一个偏置参数。（卷积核长×卷积核宽×色彩通道数量+1） 衡量的是每个特征映射对应的参数数量。
 
池化层没有参数。
 
输出层参数数量为，输入数据的维度×输出层神经元个数 + 1

代码示例如下

from keras.models import Sequential
from keras import layers


model3 = Sequential()
# 卷积层  100个特征映射，卷积核大小为7*7，(400,300,3)为输入数据的shape
model3.add(layers.Conv2D(100, (7, 7), input_shape=(400, 300, 3)))
# 最大池化层 3×3池化（也称池化步幅为3） 该层只做特征提取，没有参数
model3.add(layers.MaxPooling2D(3, 3))
# 展平层 该层也无参数
model3.add(layers.Flatten())
# 输出层 一个神经元
model3.add(layers.Dense(1))

model3.summary()

卷积层参数数量=(7×7×3+1)×100=14800。
         

from keras.utils import plot_model  
plot_model(model3, show_shapes=True)   

模型图示如下：
          

---

4.循环神经网络 RNN

每个RNN层有一个循环核。一个循环核有多个记忆体。
 
time_step不影响参数的个数。
 
设 RNN层 输入向量的维度 为input_dim
RNN层神经元个数 为 units
 
则RNN层的参数个数为 $input\_dim\times units++unit{s}^2+units$。输出层的参数数量计算方法还是常规思路。
 
为了更直观，特在下图示例中标出。 
以输入数据维度为5，记忆体个数为3，输出数据维度为5为例。神经网络包含一个隐藏层和一个输出层。
 

---

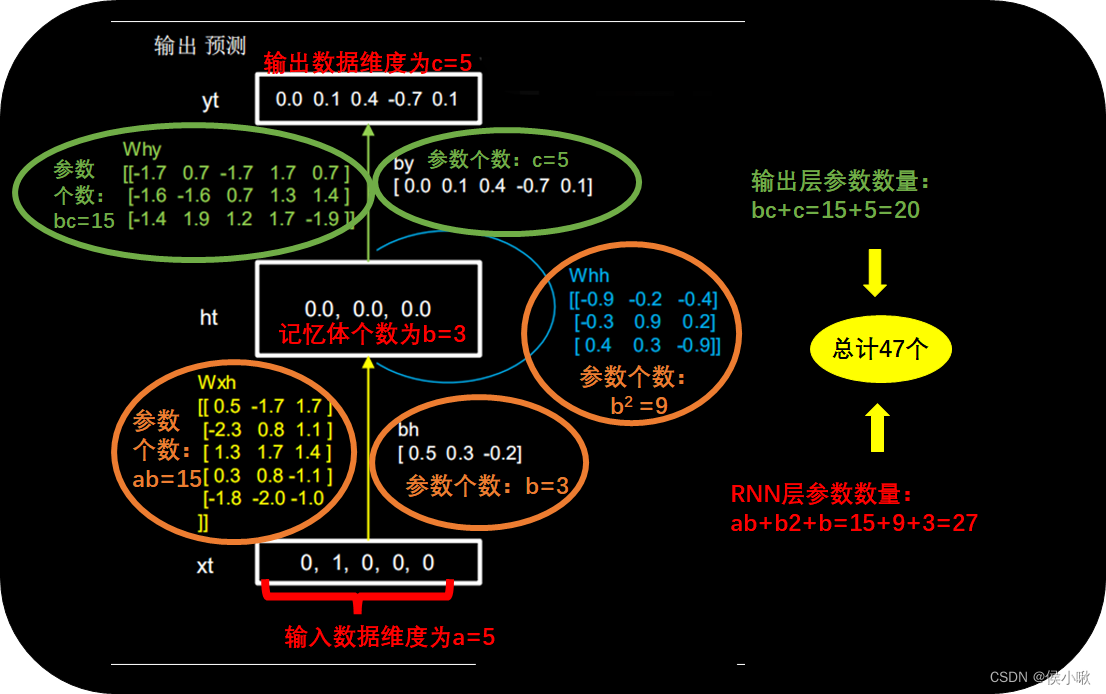
代码如下：

time_step = 10 # time_step不影响参数数量
input_dim = 5
units=3 # RNN层的神经元个数，也是记忆体的个数
output_dim = 5


model4 = Sequential()
# RNN层 5个神经元 输入数据维度为5
model4.add(layers.SimpleRNN(units=units, input_shape=(time_step,input_dim),activation='relu'))
# 输出层 一个神经元 输出数据维度为5
model4.add(layers.Dense(output_dim))

model4.summary()

         
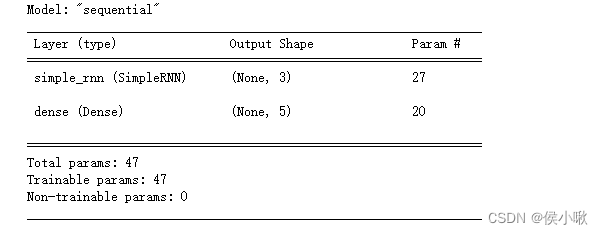
模型图示及代码：

from keras.utils import plot_model  
plot_model(model4, show_shapes=True)     

            

---

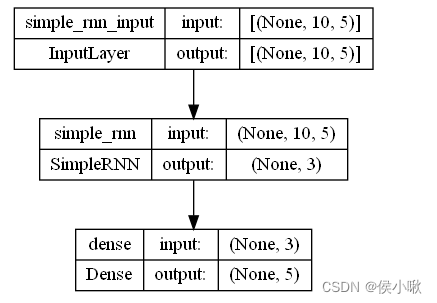
5.长短期记忆神经网络 LSTM

LSTM模型的核心是三个门和一个记忆细胞，LSTM层的参数数量为相同参数RNN模型的RNN层参数数量的4倍（单层的4倍，而非整个模型参数数量的4倍）。
输入门，遗忘门，记忆细胞，输出门的公式依次如下：
 
 输入门：$i_t=\sigma (W_i{x}_t+U_i{h}_{t-1}+b_i)$
 
 遗忘门：$f_t=\sigma (W_f{x}_t+Uf{h}_{t-1}+b_f)$
 
 内部记忆单元：$c_t^{\prime }=tanh(W_c{x}_t+U_c{h}_{t-1})$
 
        $c_t=f_t{c}_{t-1}+i_t{c}_t^{\prime }$
 

 输出门：$o_t=\sigma (W_o{x}_t+U_o{h}_{t-1}+b_o)$
 
     $h_t=o_{t}tanh(c_t)$
从上边公式可以看出，相比于上边RNN中的$W_{xh},b_h,W_{hh}$三个参数矩阵中的参数，LSTM神经网络在每个门中都多了一组$W,U,b$参数。一共多了三组，所以是4倍数量的参数。

from keras.models import Sequential
from keras.layers import Dense,LSTM

time_step = 10
input_dim = 5
units=3 # RNN层的神经元个数，也是记忆体的个数
output_dim = 5

model5 = Sequential()
# LSTM层
model5.add(LSTM(units=units,input_shape=(time_step,input_dim),activation='relu'))
# 添加输出层 
model5.add(Dense(units=output_dim, activation='softmax'))

model5.summary()

代码执行结果如下：
         
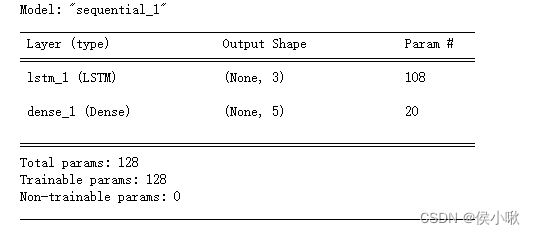
LSTM层参数数量为108，为RNN层27的四倍。加上输出层后总计有128个参数。

---

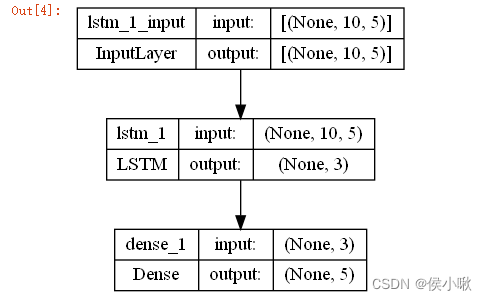
模型结构：

from keras.utils import plot_model  
plot_model(model5, show_shapes=True)     

          

---

🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ