Yan英杰的博客
悟已往之不谏 知来者之可追
目录
空间复杂度
案例1:计算BubbleSort的空间复杂度?
案例2:计算斐波那契额数列的前N项的空间复杂度
案例3:计算阶乘递归Fac的空间复杂度?
案例4:F1和F2两函数是否使用的同一块空间
案例5:计算该程序的空间复杂度
案例6:经典OJ(难度中等)
空间复杂度
 案例1:计算BubbleSort的空间复杂度?
案例1:计算BubbleSort的空间复杂度?
// 1.计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}提问:
当时我在计算该程序的空间复杂度,有个疑问,为什么不把数组算进去
这是因为,我们在计算之前,就已经开辟了数组的栈帧空间,开始前就给出了,所以不用在空间复杂度内加上数组的大小
 案例2:计算斐波那契额数列的前N项的空间复杂度
案例2:计算斐波那契额数列的前N项的空间复杂度
//计算斐波那契额数列的前N项的空间复杂度
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}分析:
我们当前的变量为0,但是我们要求第N项的空间复杂度,所以我们开辟了n+1块空间,用来计算前N项和的空间复杂度,O(N+1)为其空间复杂度,但是大O的渐进表示法,我们计算出斐波那契额数列前N项和的空间复杂度为O(N)
 案例3:计算阶乘递归Fac的空间复杂度?
案例3:计算阶乘递归Fac的空间复杂度?
//计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}
 案例4:F1和F2两函数是否使用的同一块空间
案例4:F1和F2两函数是否使用的同一块空间
//F1和F2两函数是否使用的同一块空间
void F2()
{
int b = 0;
printf("%p\n",&b);
}
void F1()
{
int a = 0;
printf("%p\n",&a);
}
int main()
{
F1();
F2();
return 0;
}解析:
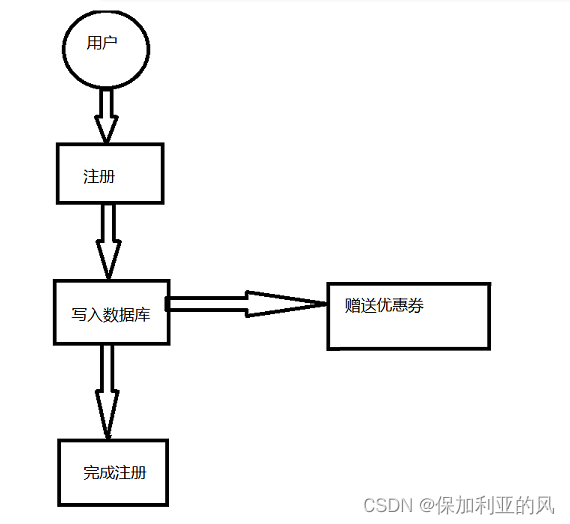
当调用F1函数时在Main函数低地址处进行压栈,当出了F1函数,函数销毁,同时它用过的栈帧空间返回到内存中,当我们再调用F2时,F2继续在Main函数低地址处压栈,所以他俩所维护的栈帧空间其实是同一块
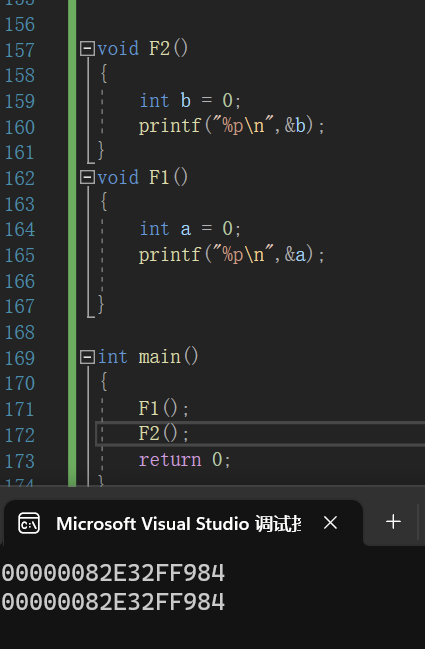
提问:
那如何修改,才能使两个函数指向不同栈帧空间?
分析:
当我们在F1中调用F2时,使得F1函数无法释放栈帧空间,F2就必须在F1低地址处压栈,此时他们两个维护的栈帧空间则不相同
图解:
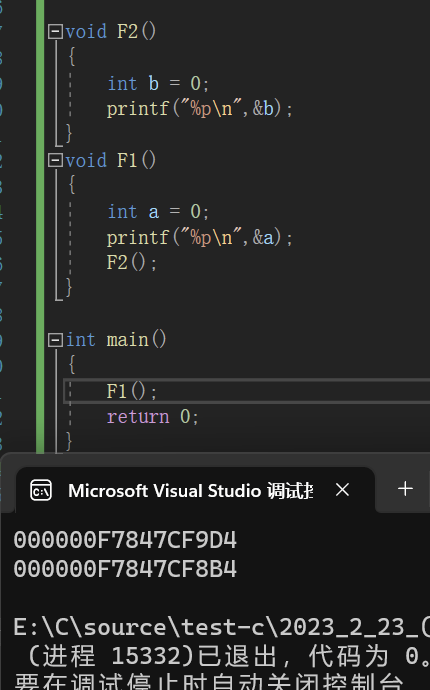
 案例5:计算该程序的空间复杂度
案例5:计算该程序的空间复杂度
//计算该程序的空间复杂度
long long Fib(size_t N)
{
if (N<3)
{
return 1;
}
return Fib(N-1) - Fib(N-2);
}

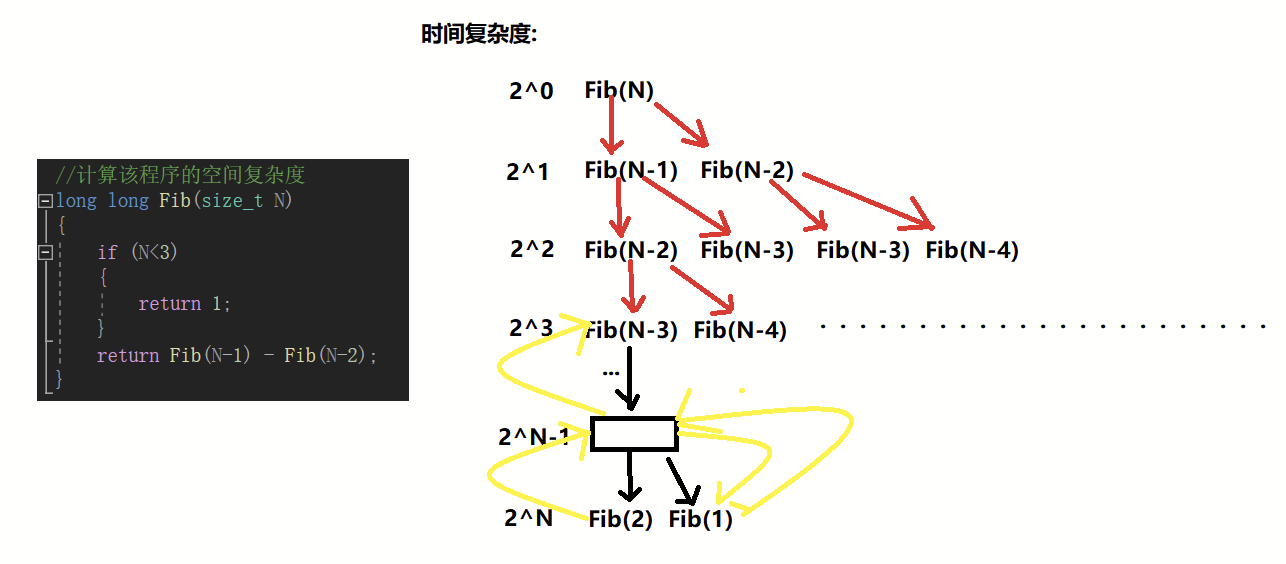
注:时间一去不复返无法重复利用,但是空间用了之后归还,可以重复利用
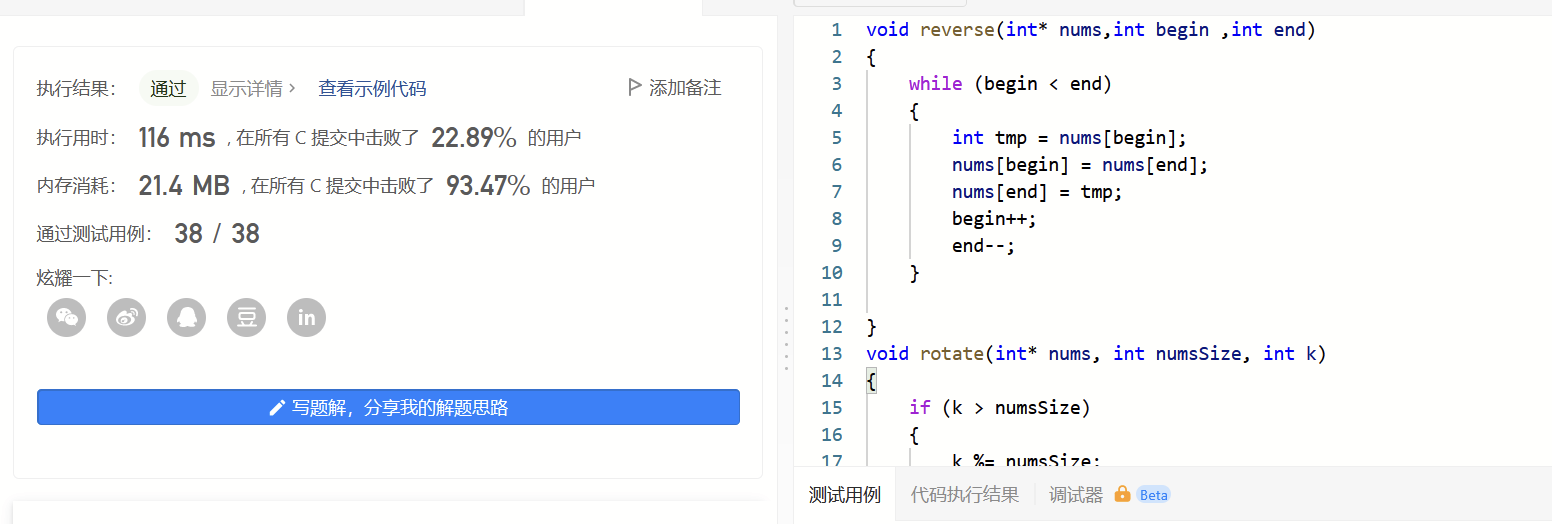
 案例6:经典OJ(难度中等)
案例6:经典OJ(难度中等)
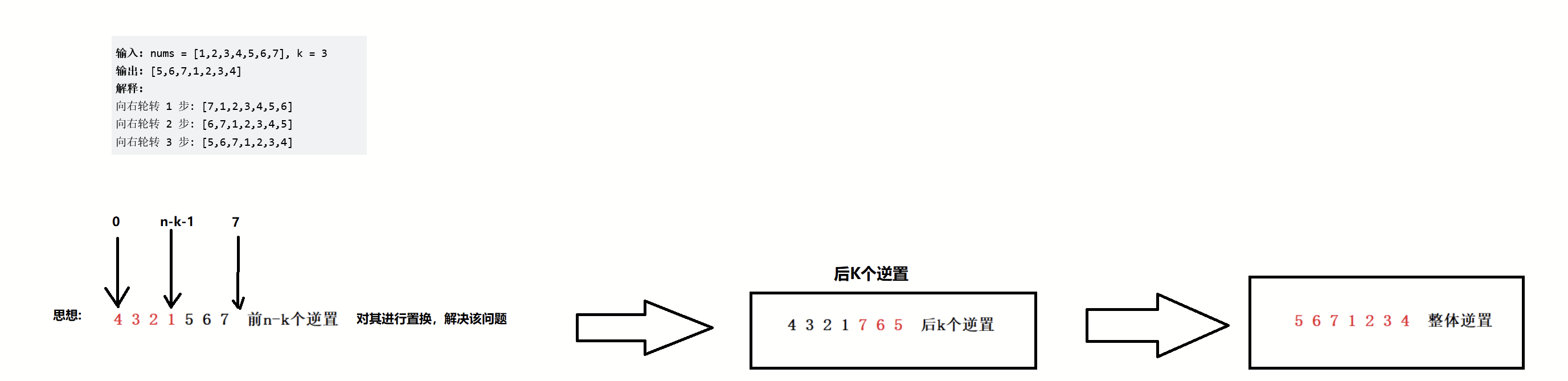
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
图解:
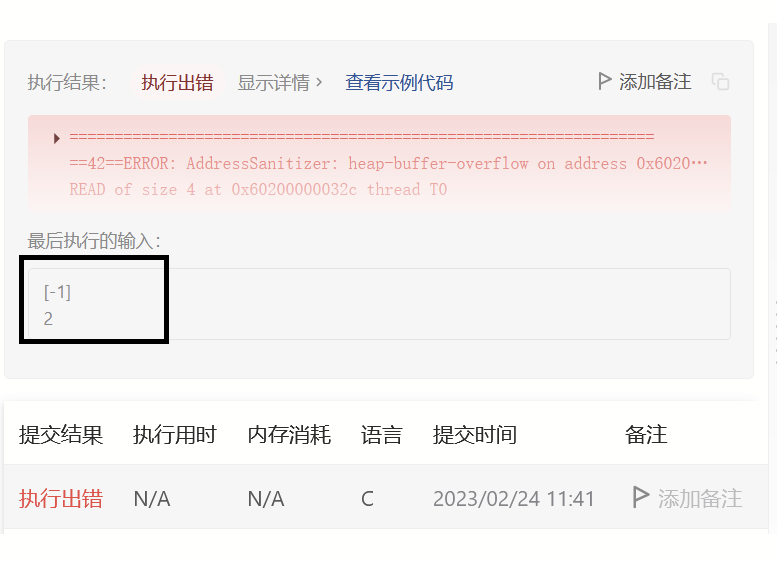
错误示范:
void reverse(int* nums,int begin ,int end) { while (begin < end) { int tmp = nums[begin]; nums[begin] = nums[end]; nums[end] = tmp; begin++; end--; } } void rotate(int* nums, int numsSize, int k) { reverse(nums,0,numsSize-k-1); reverse(nums,numsSize-k,numsSize-1); reverse(nums, 0, numsSize - 1); }
void reverse(int* nums,int begin ,int end)
{
while (begin < end)
{
int tmp = nums[begin];
nums[begin] = nums[end];
nums[end] = tmp;
begin++;
end--;
}
}
void rotate(int* nums, int numsSize, int k)
{
if (k > numsSize)
{
k %= numsSize;
}
reverse(nums,0,numsSize-k-1);
reverse(nums,numsSize-k,numsSize-1);
reverse(nums, 0, numsSize - 1);
}