算法拾遗二十七之窗口最大值或最小值的更新结构
- 滑动窗口
- 题目一
- 题目二
- 题目三
- 题目四
滑动窗口
第一种:R++,R右动,数会从右侧进窗口
第二种:L++,L右动,数从左侧出窗口
题目一

arr是N,窗口大小为W,会返回N-W+1个数
// 暴力的对数器方法
public static int[] right(int[] arr, int w) {
if (arr == null || w < 1 || arr.length < w) {
return null;
}
int N = arr.length;
int[] res = new int[N - w + 1];
int index = 0;
//第一个窗口0-(w-1)
int L = 0;
int R = w - 1;
while (R < N) {
int max = arr[L];
for (int i = L + 1; i <= R; i++) {
max = Math.max(max, arr[i]);
}
res[index++] = max;
L++;
R++;
}
return res;
}
public static int[] getMaxWindow(int[] arr, int w) {
if (arr == null || w < 1 || arr.length < w) {
return null;
}
// qmax 双端队列就是窗口最大值的更新结构
// 里面放下标方便更新
LinkedList<Integer> qmax = new LinkedList<Integer>();
//N-w+1
int[] res = new int[arr.length - w + 1];
int index = 0;
//R表示窗口的右边界
for (int R = 0; R < arr.length; R++) {
//双端队列上最尾巴上的元素是不是小于当前的值的,如果小于等于则从尾巴弹出
while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) {
qmax.pollLast();
}
qmax.addLast(R);
//窗口的过期数的下标
if (qmax.peekFirst() == R - w) {
qmax.pollFirst();
}
//形成窗口的时候,表示需要收集答案,每一步都收集一个答案
if (R >= w - 1) {
res[index++] = arr[qmax.peekFirst()];
}
}
return res;
}
题目二

思路:
如果L-R已经达标了,那么L-R内部的所有子数组都是达标的,因为L-R范围内部的子数组max在变小,min在变大。
如果L-R范围不达标,那么L往左扩大范围和R往右边扩大范围都不达标。
准备一个窗口内最大值的更新结构,同样准备窗口内最小值的更新结构。【同时使用两个结构维持窗口内的最大和最小】
步骤:
1、L不动,R如果满足【L-R范围的最大值和最小值的差值如果都满足小于等于num】则R一直往右边扩
,直到不满足条件为止。(注意此时是L在0为止,算出从零开始的子数组有多少个累加进结果)
2、L向右移动一位,看看R能不能往右扩,再算从L+1位置到能构成条件的子数组有多少个,再累加进结果。
// 暴力的对数器方法
public static int right(int[] arr, int sum) {
if (arr == null || arr.length == 0 || sum < 0) {
return 0;
}
int N = arr.length;
int count = 0;
for (int L = 0; L < N; L++) {
for (int R = L; R < N; R++) {
int max = arr[L];
int min = arr[L];
for (int i = L + 1; i <= R; i++) {
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
if (max - min <= sum) {
count++;
}
}
}
return count;
}
public static int num(int[] arr, int sum) {
if (arr == null || arr.length == 0 || sum < 0) {
return 0;
}
int N = arr.length;
int count = 0;
LinkedList<Integer> maxWindow = new LinkedList<>();
LinkedList<Integer> minWindow = new LinkedList<>();
int R = 0;
for (int L = 0; L < N; L++) {
//依次尝试窗口为0开始,1开始。。。。
while (R < N) {
//R扩到初次不达标的时候停
while (!maxWindow.isEmpty() && arr[maxWindow.peekLast()] <= arr[R]) {
//维护从大到小列表
maxWindow.pollLast();
}
maxWindow.addLast(R);
while (!minWindow.isEmpty() && arr[minWindow.peekLast()] >= arr[R]) {
//维护从小到大列表
minWindow.pollLast();
}
minWindow.addLast(R);
//最大值减去最小值大于sum则初次不达标了停止
if (arr[maxWindow.peekFirst()] - arr[minWindow.peekFirst()] > sum) {
break;
} else {
R++;
}
}
//加结果
count += R - L;
//如果L即将过期则弹出窗口对应值
if (maxWindow.peekFirst() == L) {
maxWindow.pollFirst();
}
if (minWindow.peekFirst() == L) {
minWindow.pollFirst();
}
}
return count;
}
// for test
public static int[] generateRandomArray(int maxLen, int maxValue) {
int len = (int) (Math.random() * (maxLen + 1));
int[] arr = new int[len];
for (int i = 0; i < len; i++) {
arr[i] = (int) (Math.random() * (maxValue + 1)) - (int) (Math.random() * (maxValue + 1));
}
return arr;
}
// for test
public static void printArray(int[] arr) {
if (arr != null) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int maxLen = 100;
int maxValue = 200;
int testTime = 100000;
System.out.println("测试开始");
for (int i = 0; i < testTime; i++) {
int[] arr = generateRandomArray(maxLen, maxValue);
int sum = (int) (Math.random() * (maxValue + 1));
int ans1 = right(arr, sum);
int ans2 = num(arr, sum);
if (ans1 != ans2) {
System.out.println("Oops!");
printArray(arr);
System.out.println(sum);
System.out.println(ans1);
System.out.println(ans2);
break;
}
}
System.out.println("测试结束");
}
题目三

给定两个数组一个是gas数组,一个是cost数组,
0号加油站有1单位的油,但是跑到加油站2需要耗费两单位的油,从哪个加油站开始能转完一圈?
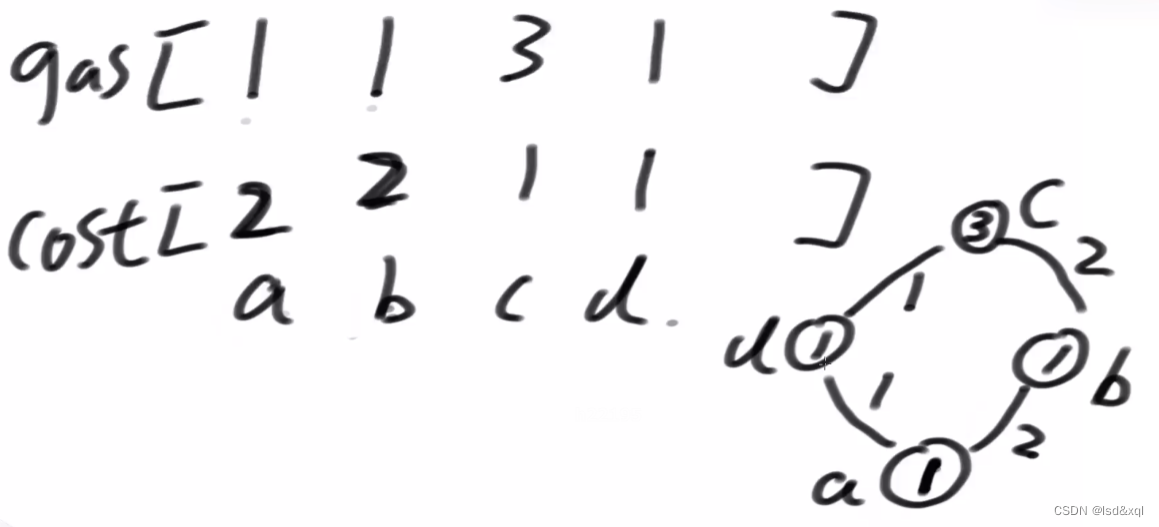
如上图,只能通过从C出发才能跑完一圈
思路:
加工出一个arr数组,就是gas-cost数组,做一个简化
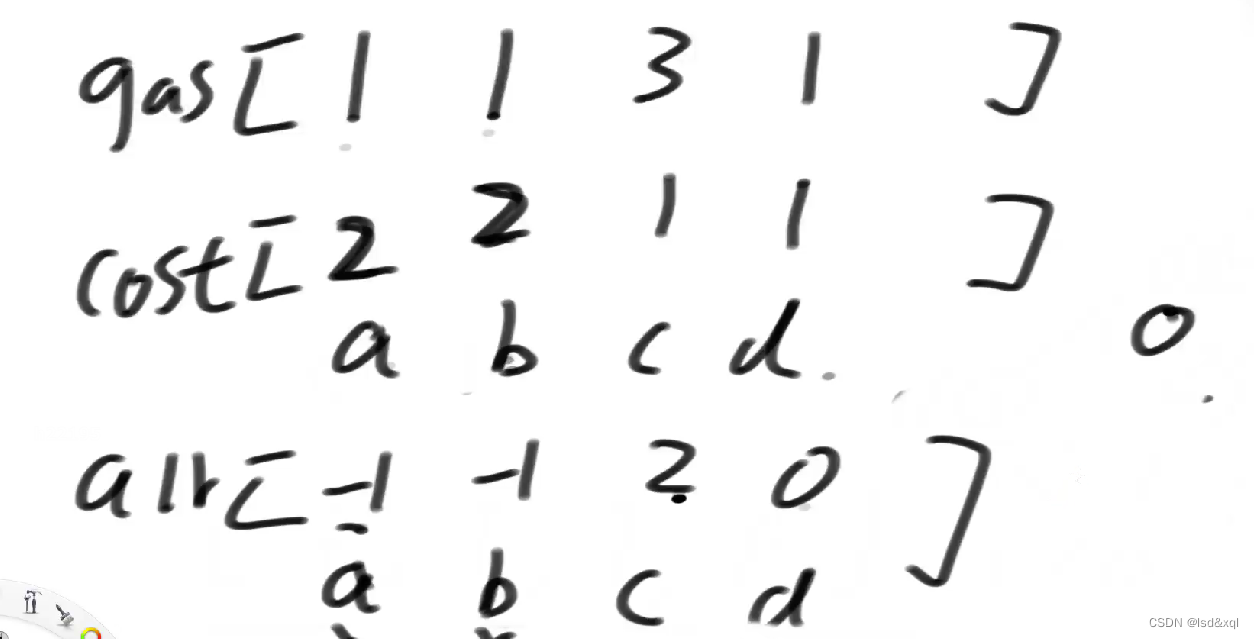
再看如下例子
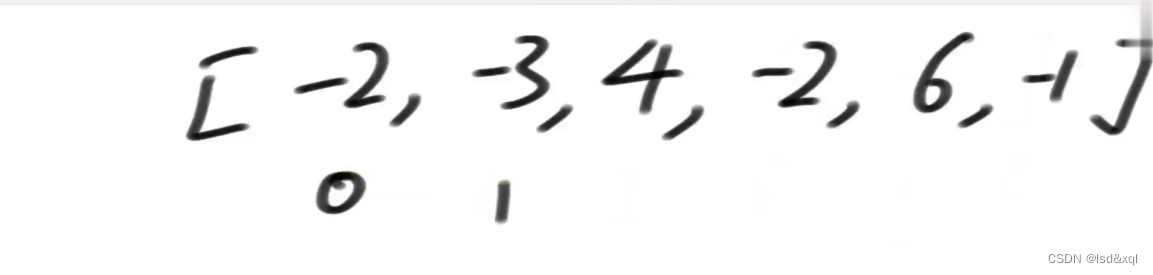
暴力解:搞定循环数组的遍历,从0位置出发找是否有解,从1位置出发找是否有解依次找下去
方法二:
1、先算累加和:
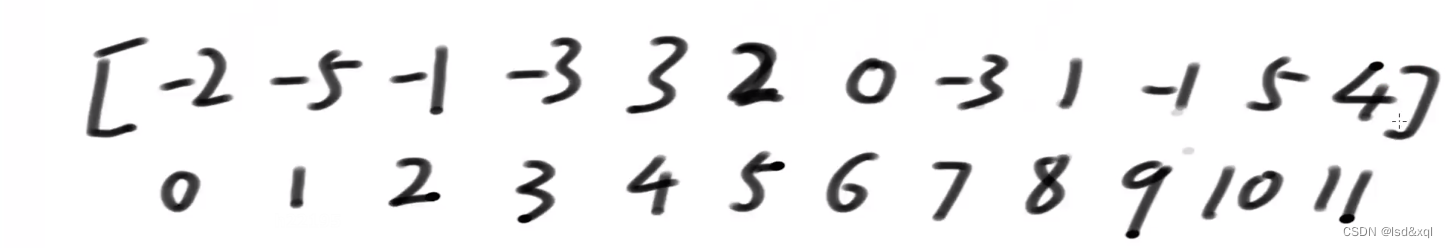
这样写的目的:从零出发一直累加到五之前,可以判断从0位置出发不是良好出发点,再看从1位置出发依次累加
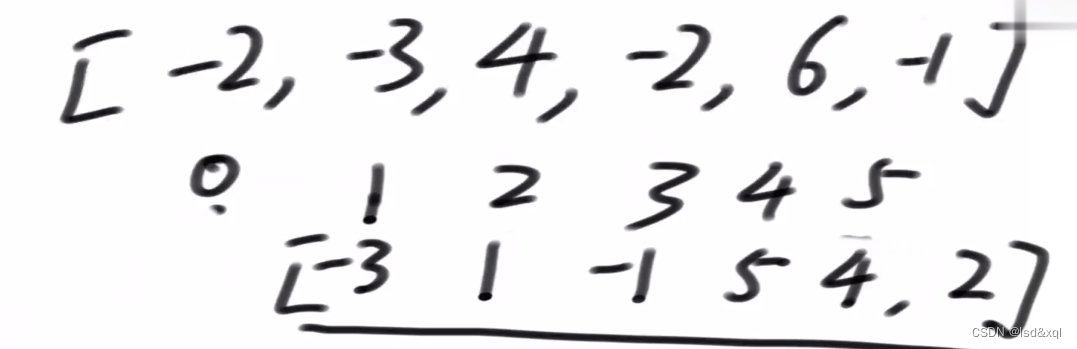
里面包含负数可以知道它不是一个良好出发点,如上图这个数组就是算从零位置开始计算的累加和得到的那个数组减去-2得到的数组。
做一个两倍长度的数组就是想让它所有原始数组中出发的那个位置,在长数组中能把它原始的累加和给加工出来
则每次计算后续的出发点的数组内容时,则减去前一个就能得到了

搞一个窗口,这个窗口就是原始数组的长度,窗口的最小值(最薄弱点)是-5减去出发位置前面一个数,从而还原出原始数组累加和最薄弱点,还原出的结果还是小于0则不是良好出发点,还原出的结果不小于0则是良好出发点
如0位置出发薄弱点为-5,还原出原始累加和为-5-0还是小于0不是良好出发点。
这道题,
要想到窗口往最大值和最小值上面靠,进而想到累加和最薄弱的点
// 测试链接:https://leetcode.com/problems/gas-station
public class GasStation {
// 这个方法的时间复杂度O(N),额外空间复杂度O(N)
public static int canCompleteCircuit(int[] gas, int[] cost) {
boolean[] good = goodArray(gas, cost);
for (int i = 0; i < gas.length; i++) {
if (good[i]) {
return i;
}
}
return -1;
}
public static boolean[] goodArray(int[] g, int[] c) {
int N = g.length;
int M = N << 1;
int[] arr = new int[M];
for (int i = 0; i < N; i++) {
arr[i] = g[i] - c[i];
arr[i + N] = g[i] - c[i];
}
for (int i = 1; i < M; i++) {
arr[i] += arr[i - 1];
}
LinkedList<Integer> w = new LinkedList<>();
for (int i = 0; i < N; i++) {
while (!w.isEmpty() && arr[w.peekLast()] >= arr[i]) {
w.pollLast();
}
w.addLast(i);
}
boolean[] ans = new boolean[N];
for (int offset = 0, i = 0, j = N; j < M; offset = arr[i++], j++) {
if (arr[w.peekFirst()] - offset >= 0) {
ans[i] = true;
}
if (w.peekFirst() == i) {
w.pollFirst();
}
while (!w.isEmpty() && arr[w.peekLast()] >= arr[j]) {
w.pollLast();
}
w.addLast(j);
}
return ans;
}
}
题目四

public class Code04_MinCoinsOnePaper {
public static int minCoins(int[] arr, int aim) {
return process(arr, 0, aim);
}
public static int process(int[] arr, int index, int rest) {
if (rest < 0) {
return Integer.MAX_VALUE;
}
if (index == arr.length) {
return rest == 0 ? 0 : Integer.MAX_VALUE;
} else {
int p1 = process(arr, index + 1, rest);
int p2 = process(arr, index + 1, rest - arr[index]);
if (p2 != Integer.MAX_VALUE) {
p2++;
}
return Math.min(p1, p2);
}
}
// dp1时间复杂度为:O(arr长度 * aim)
public static int dp1(int[] arr, int aim) {
if (aim == 0) {
return 0;
}
int N = arr.length;
int[][] dp = new int[N + 1][aim + 1];
dp[N][0] = 0;
for (int j = 1; j <= aim; j++) {
dp[N][j] = Integer.MAX_VALUE;
}
for (int index = N - 1; index >= 0; index--) {
for (int rest = 0; rest <= aim; rest++) {
int p1 = dp[index + 1][rest];
int p2 = rest - arr[index] >= 0 ? dp[index + 1][rest - arr[index]] : Integer.MAX_VALUE;
if (p2 != Integer.MAX_VALUE) {
p2++;
}
dp[index][rest] = Math.min(p1, p2);
}
}
return dp[0][aim];
}
public static class Info {
public int[] coins;
public int[] zhangs;
public Info(int[] c, int[] z) {
coins = c;
zhangs = z;
}
}
public static Info getInfo(int[] arr) {
HashMap<Integer, Integer> counts = new HashMap<>();
for (int value : arr) {
if (!counts.containsKey(value)) {
counts.put(value, 1);
} else {
counts.put(value, counts.get(value) + 1);
}
}
int N = counts.size();
int[] coins = new int[N];
int[] zhangs = new int[N];
int index = 0;
for (Entry<Integer, Integer> entry : counts.entrySet()) {
coins[index] = entry.getKey();
zhangs[index++] = entry.getValue();
}
return new Info(coins, zhangs);
}
// dp2时间复杂度为:O(arr长度) + O(货币种数 * aim * 每种货币的平均张数)
public static int dp2(int[] arr, int aim) {
if (aim == 0) {
return 0;
}
// 得到info时间复杂度O(arr长度)
Info info = getInfo(arr);
int[] coins = info.coins;
int[] zhangs = info.zhangs;
int N = coins.length;
int[][] dp = new int[N + 1][aim + 1];
dp[N][0] = 0;
for (int j = 1; j <= aim; j++) {
dp[N][j] = Integer.MAX_VALUE;
}
// 这三层for循环,时间复杂度为O(货币种数 * aim * 每种货币的平均张数)
for (int index = N - 1; index >= 0; index--) {
for (int rest = 0; rest <= aim; rest++) {
dp[index][rest] = dp[index + 1][rest];
for (int zhang = 1; zhang * coins[index] <= aim && zhang <= zhangs[index]; zhang++) {
if (rest - zhang * coins[index] >= 0
&& dp[index + 1][rest - zhang * coins[index]] != Integer.MAX_VALUE) {
dp[index][rest] = Math.min(dp[index][rest], zhang + dp[index + 1][rest - zhang * coins[index]]);
}
}
}
}
return dp[0][aim];
}
// dp3时间复杂度为:O(arr长度) + O(货币种数 * aim)
// 优化需要用到窗口内最小值的更新结构
public static int dp3(int[] arr, int aim) {
if (aim == 0) {
return 0;
}
// 得到info时间复杂度O(arr长度)
Info info = getInfo(arr);
int[] c = info.coins;
int[] z = info.zhangs;
int N = c.length;
int[][] dp = new int[N + 1][aim + 1];
dp[N][0] = 0;
for (int j = 1; j <= aim; j++) {
dp[N][j] = Integer.MAX_VALUE;
}
// 虽然是嵌套了很多循环,但是时间复杂度为O(货币种数 * aim)
// 因为用了窗口内最小值的更新结构
for (int i = N - 1; i >= 0; i--) {
for (int mod = 0; mod < Math.min(aim + 1, c[i]); mod++) {
// 当前面值 X
// mod mod + x mod + 2*x mod + 3 * x
LinkedList<Integer> w = new LinkedList<>();
w.add(mod);
dp[i][mod] = dp[i + 1][mod];
for (int r = mod + c[i]; r <= aim; r += c[i]) {
while (!w.isEmpty() && (dp[i + 1][w.peekLast()] == Integer.MAX_VALUE
|| dp[i + 1][w.peekLast()] + compensate(w.peekLast(), r, c[i]) >= dp[i + 1][r])) {
w.pollLast();
}
w.addLast(r);
int overdue = r - c[i] * (z[i] + 1);
if (w.peekFirst() == overdue) {
w.pollFirst();
}
dp[i][r] = dp[i + 1][w.peekFirst()] + compensate(w.peekFirst(), r, c[i]);
}
}
}
return dp[0][aim];
}
public static int compensate(int pre, int cur, int coin) {
return (cur - pre) / coin;
}
// 为了测试
public static int[] randomArray(int N, int maxValue) {
int[] arr = new int[N];
for (int i = 0; i < N; i++) {
arr[i] = (int) (Math.random() * maxValue) + 1;
}
return arr;
}
// 为了测试
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// 为了测试
public static void main(String[] args) {
int maxLen = 20;
int maxValue = 30;
int testTime = 300000;
System.out.println("功能测试开始");
for (int i = 0; i < testTime; i++) {
int N = (int) (Math.random() * maxLen);
int[] arr = randomArray(N, maxValue);
int aim = (int) (Math.random() * maxValue);
int ans1 = minCoins(arr, aim);
int ans2 = dp1(arr, aim);
int ans3 = dp2(arr, aim);
int ans4 = dp3(arr, aim);
if (ans1 != ans2 || ans3 != ans4 || ans1 != ans3) {
System.out.println("Oops!");
printArray(arr);
System.out.println(aim);
System.out.println(ans1);
System.out.println(ans2);
System.out.println(ans3);
System.out.println(ans4);
break;
}
}
System.out.println("功能测试结束");
System.out.println("==========");
int aim = 0;
int[] arr = null;
long start;
long end;
int ans2;
int ans3;
System.out.println("性能测试开始");
maxLen = 30000;
maxValue = 20;
aim = 60000;
arr = randomArray(maxLen, maxValue);
start = System.currentTimeMillis();
ans2 = dp2(arr, aim);
end = System.currentTimeMillis();
System.out.println("dp2答案 : " + ans2 + ", dp2运行时间 : " + (end - start) + " ms");
start = System.currentTimeMillis();
ans3 = dp3(arr, aim);
end = System.currentTimeMillis();
System.out.println("dp3答案 : " + ans3 + ", dp3运行时间 : " + (end - start) + " ms");
System.out.println("性能测试结束");
System.out.println("===========");
System.out.println("货币大量重复出现情况下,");
System.out.println("大数据量测试dp3开始");
maxLen = 20000000;
aim = 10000;
maxValue = 10000;
arr = randomArray(maxLen, maxValue);
start = System.currentTimeMillis();
ans3 = dp3(arr, aim);
end = System.currentTimeMillis();
System.out.println("dp3运行时间 : " + (end - start) + " ms");
System.out.println("大数据量测试dp3结束");
System.out.println("===========");
System.out.println("当货币很少出现重复,dp2比dp3有常数时间优势");
System.out.println("当货币大量出现重复,dp3时间复杂度明显优于dp2");
System.out.println("dp3的优化用到了窗口内最小值的更新结构");
}
}