学习了二叉树，今天来整理一下笔记吧！

一：树的理解

树的度是不限制的，一个双亲结点可以有很多子节点，但是子节点是不能交叉的，也就是不能有环。

树的的最大层次叫做这棵树的深度或者高度；

树的代码表示：

用代码如何连接这些数据，让他和树有一样的访问顺序呢

可以用左孩子右兄弟的算法：

typedef int DataType;
struct Node{
    struct Node* child;
    struct Node* brother;
    DataType x;
};

每一个结点含有有两个指向：指向孩子和兄弟结点

windos的文件管理使用的结构就是树

二、二叉树的个人理解

二叉树也是树，是每一个结点的孩子数为一个，两个，没有孩子。

二叉树的左右孩子是有区分的，不能颠倒，有序树

满二叉树：

除了最后一层的结点，其他每一层的结点都是有两个孩子，它的结点总数是2^k-1;

完全二叉树：

倒数第二层的结点，存在有的结点不是有两个孩子。最后一层的结点数从左到右必须连续；

二叉树的一些性质：

根节点为1：第i层的节点数最大为2^（i-1）

深度为k的二叉树的总结点数为：2^k-1;

度为0的结点数比度为2的节点数多一个：n0 = n2+1；

具有n各节点的二叉树，它的深度为：k = log2（n+1）

若二叉树上下，左右的顺序标号，则序号为i的结点，它的双亲是（i-1）/2

它的左孩子为2*i+1，右孩子为2*i+2，但是总数不能超过总结点数n；

三、二叉树的存储结构

逻辑结构方便我们记忆的就是为树的样子；

顺序存储：

二、链式存储：

每一个结点包含左孩子和右孩子和存储的数据x：

typedef int TypeData;
struct BinaryTreeNode{
    struct TreeNode* left;
    struct TreeNode* right;
    TypeData x;
}; 

完全二叉树的顺序结构的实现：

完全二叉树适合用顺序存储来实现；

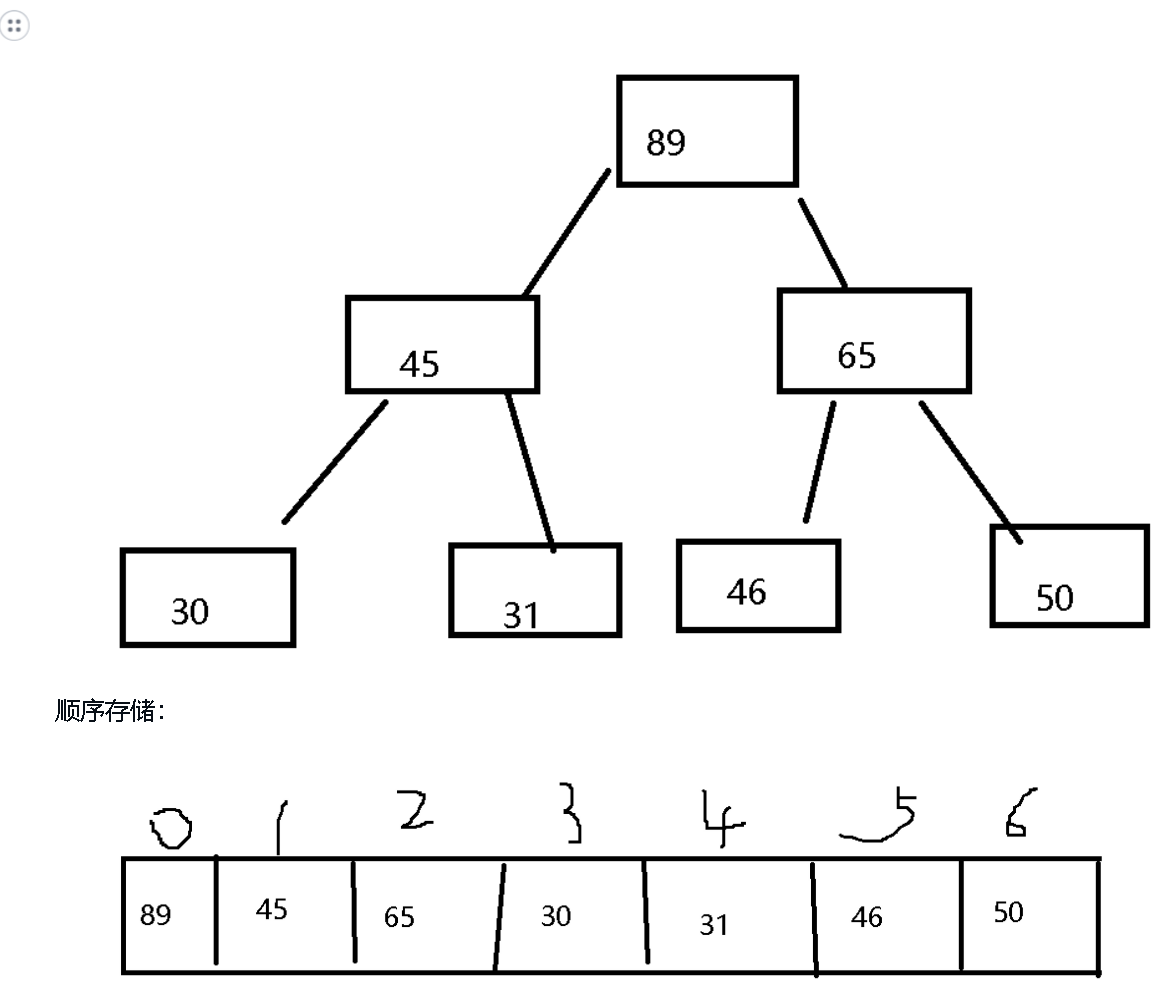
将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。上图就是大堆； 堆的性质： 堆中某个节点的值总是不大于或不小于其父节点的值； 堆总是一棵完全二叉树。