前言:给定一个链表,判断是否为循环链表并找环形链表的入口点



首先我们需要知道什么是双向循环链表,具体如下图所示。
对于链表,我们如何去判断链表是循环链表呢?又寻找入环点呢?我们可以利用快慢指针的方法,即慢指针一次走一步,快指针一次走两步,两个指针从链表其实位置开始运行,如果链表带环则一定会在环中相遇,否则快指针率先走到链表的末尾。为什么呢?原理是什么呢?我们利用图解分析一波?
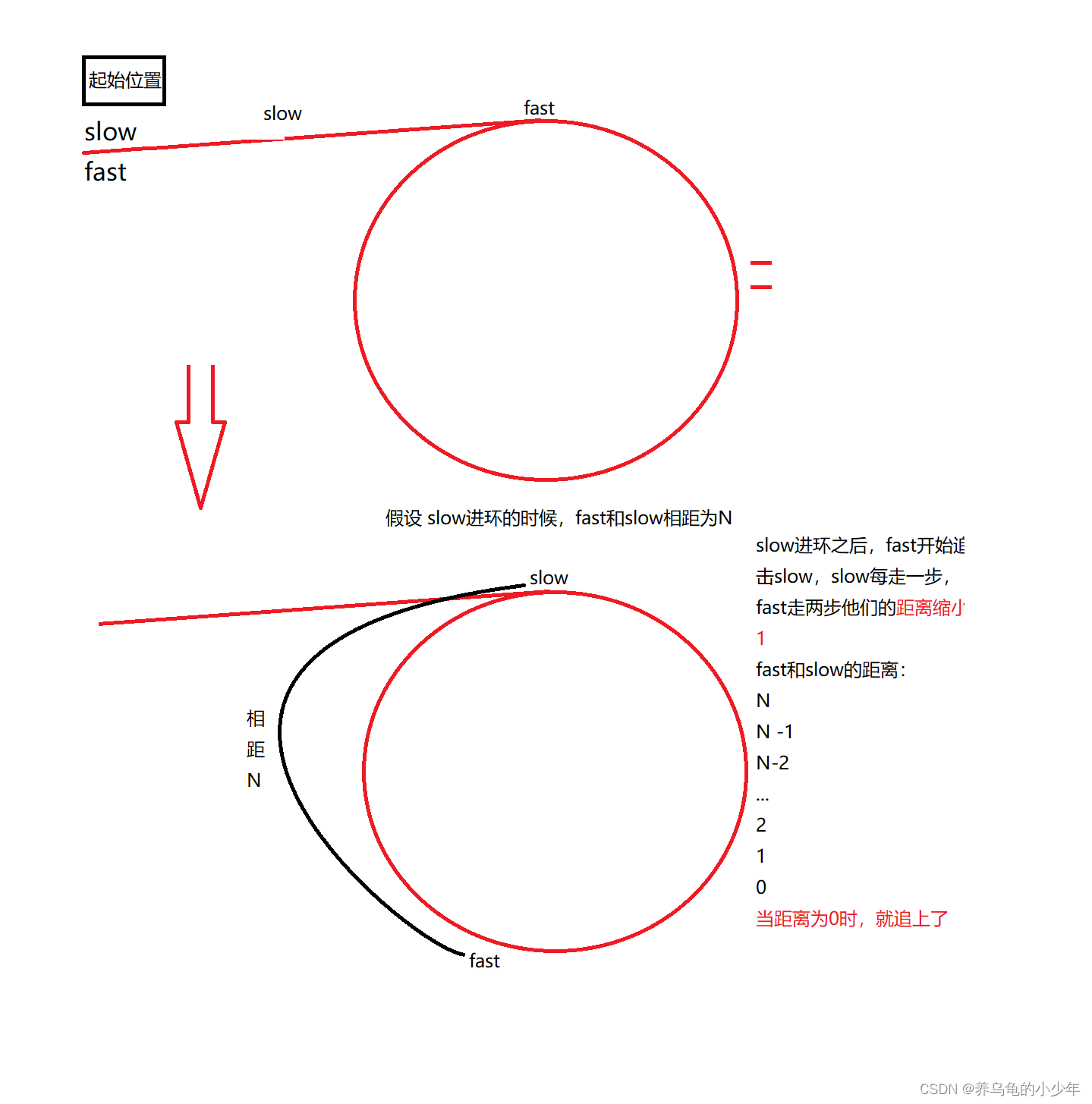
问题2:如果slow走一步,fast走三步,他们还会相遇吗?会不会错过呢?我们图解分析一下:
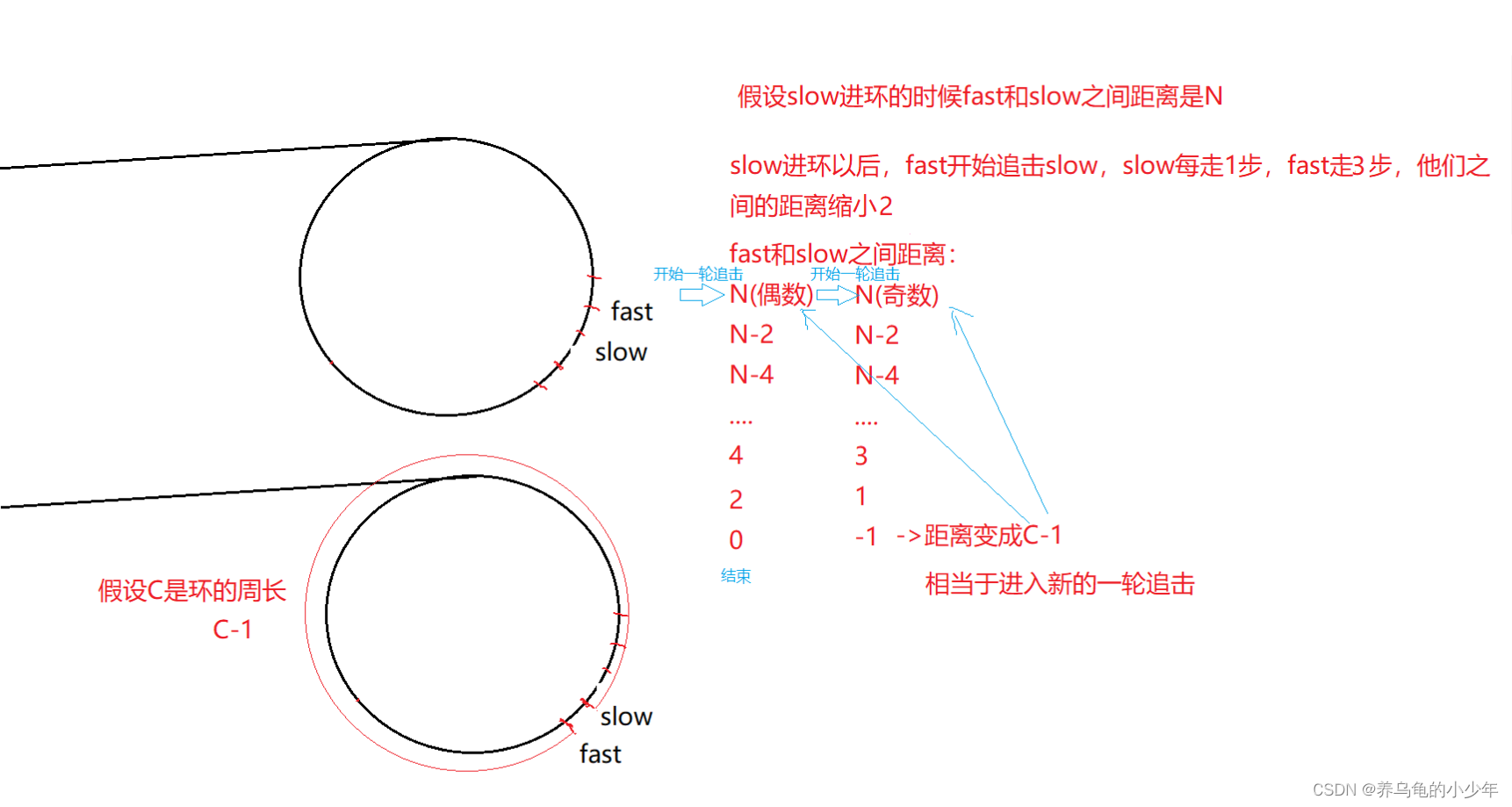
开始追击的时候,他们fast每走一次,他们之间的距离就会缩小2,这时候就要分N奇偶的情况了,为偶的话一定会相遇,为奇的话,每次减少2步,最后fast会超越slow一步,假设环的周长是C的话也就是 fast和slow之间 会相距C - 1步,这时候又要分C-1奇偶情况,为偶数的话,一定会相遇,为奇数的话,就会陷入奇数循环,永远不会为偶。也就不会相遇。
问题3:如何找入口点呢?
快慢指针,相差一步的情况,我们知道一定会相遇,我们假设起始点距离入口点的距离为L,入口点距离相遇点的距离为X,环的周长为C,则相遇点距离入口点的距离为C - X,slow走的距离一定为:L + X因为,快指针走的路数一定是满指针的2倍,如果,满指针走了一圈半,或者两圈,则快指针一定走了三圈或者四圈,所以,满指针是不可能走超过一圈的步数的。那快指针呢?快指针走了多少呢?是 L + C + X ?因为是慢指针步数的二倍,所以是 2 * (L + X) = L + C + X 推出来L = C - X ?这真的合理吗 肯定是不合理的 我们可以画个图推翻它,如下所示:
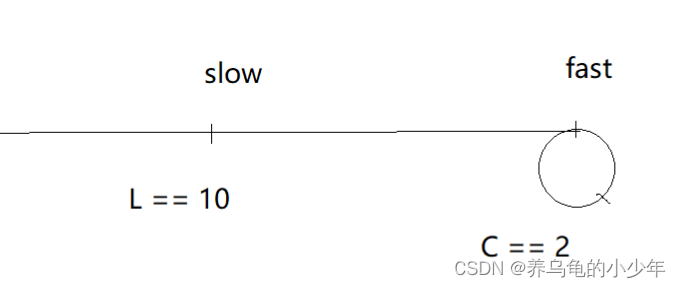
当环很小的时候,譬如只有两个节点,而L为10个节点 fast每次两步,都绕九个环了,慢指针才进环,所以上面的推理是不合理的。

fast正确走的步数应该是 L + n * C + X,根据二倍的关系的话。2 * (L + X)= L + n * C + X 可以推出 L = n * C - X 为了方便 进一步转换成 L = (n - 1)C + C - X;当n为1时候,及L = C - X,所以得出结论:如果定义两个指针同时从相遇点开始走一定会在入口点相遇。详细代码如下:
解题思路:
如果链表存在环,则fast和slow会在环内相遇,定义相遇点到入口点的距离为X,定义环的长度为C,定义头到入口的距离为L,fast在slow进入环之后一圈内追上slow,则会得知:
slow所走的步数为:L + X
fast所走的步数为:L + X + N * C
并且fast所走的步数为slow的两倍,故:
2*(L + X) = L + X + N * C
即: L = N * C - X
所以从相遇点开始slow继续走,让一个指针从头开始走,相遇点即为入口节点
*/
typedef struct ListNode Node;
struct ListNode *detectCycle(struct ListNode *head) {
Node* slow = head;
Node* fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
//走到相遇点
if(slow == fast)
{
// 求环的入口点
Node* meet = slow;
Node* start = head;
while(meet != start)
{
meet = meet->next;
start = start->next;
}
return meet;
}
}
return NULL;
}