文章目录

一、查找
- 1. 无序表的顺序查找
- 2. 折半查找
- 3. 分块查找
- 4. 二叉排序树BST
- 5. 哈希表查找
二、排序
- 1. 不带哨兵的直接插入排序
- 2. 带哨兵的直接插入排序
- 3. 带哨兵、折半查找的直接插入排序
- 4. 希尔排序
- 5. 冒泡排序
- 6. 快速排序
- 7. 选择排序
- 8. 堆排序
- 9. 归并排序
二叉树
- 1. 递归先序遍历
- 2. 非递归先序遍历
- 3. 递归中序遍历
- 4. 非递归中序遍历
- 5. 递归后序遍历
- 6. 非递归后序遍历
- 7. 广度遍历二叉树
- 8. 深度遍历

一、查找

1. 无序表的顺序查找

把待查关键字key存入表头（哨兵），从后向前逐个比较，可免去查找过程中每一步都要检测是否查找完毕，加快速度。

// 下标从1开始，头节点为空
public static int sentrySearch(int[] arr, int target){
	arr[0] = target;
	int index = arr.length-1;
	while(arr[index] != target){
		--index;
	}
	if(index == 0) return -1;
	return index;
}

空间复杂度：O(1)
时间复杂度：O(n)
平均查找长度：ASL =（n+1）/ 2

2. 折半查找

首先将给定值key与表中中间位置的元素比较，若相等则查找成功，返回该元素的存储位置；若不等则所需查找的元素只能在中间元素以外的前半部分或后半部分。

public static int Sort(int[] nums, int target){
	int low = 0;
	int high = nums.length;
	while(low < high){
		mid = (low + high) / 2;
		if(target == nums[mid]) return mid;
		if(target < nums[mid]) high = mid-1;
		if(target > nums[mid]) low = mid+1;
	}
	return -1
}

空间复杂度：O(1)
时间复杂度：O( $log_2$ n)
平均查找长度：ASL = $log_2$ （n+1）

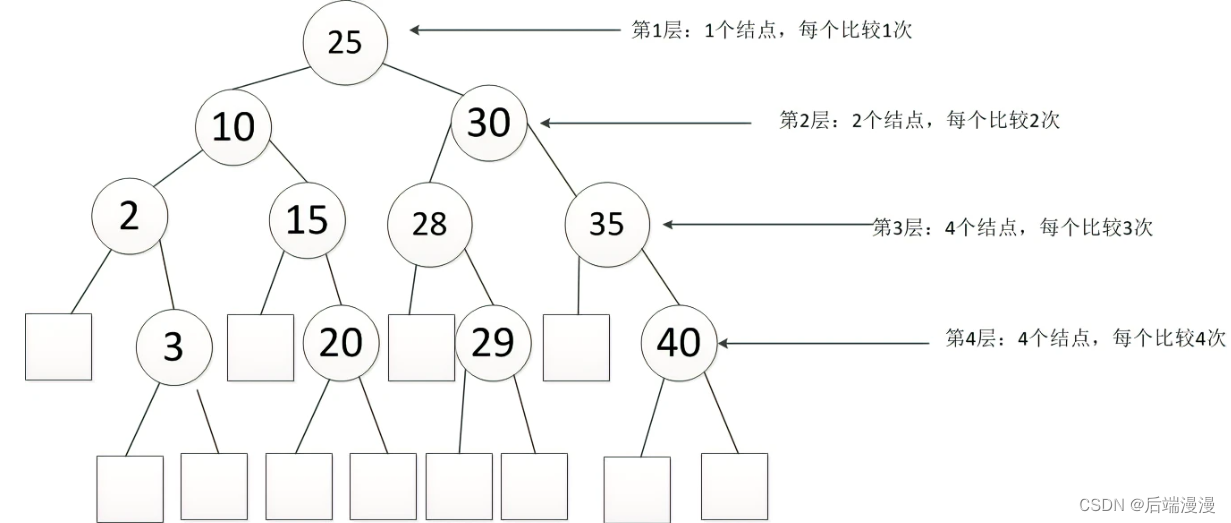
3. 分块查找

分块查找又称索引顺序查找，它是顺序查找的一种改进方法：将n个数据元素“按块有序”划分为m块（m<=n）。每一块中的数据元素不必有序，但块与块之间必须“按块有序”，即第1快中的任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都小于第3块中的任一元素，……

查找分两部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；然后在已确定的快中用顺序法进行查找。

@AllArgsConstructor
class IndexItem {
	public int index; //值比较的索引
 	public int start; //开始位置
	public int length;//块元素长度(非空)
}

public int indexSearch(int key){
	int[] mainList = new int[]{
		22, 12, 13, 8, 9, 20, 
		33, 42, 44, 38, 24, 48,
		60, 58, 74, 49, 86, 53
	}

	IndexItem[] indexItemList = new IndexItem[]{
		new IndexItem(22,1,6),
		new IndexItem(48,7,6),
		new IndexItem(86,13,6);
	}

	// 第一步，查找在哪一块
	int index = 0;
	for(;index < indexItemList.length; index++){
		if(indexItemList[index].index >= key ) break;
	} 

	int num = 0;
	for(int i=0; i<index; i++){
		num += indexlist[i].length;
	}

	for(int i=num; i<num+indexItemList.length; i++){
		if(MainList[i] == key) return i;
	}

	return -1;
}

时间复杂度：O(log(m)+n/m)，n个数据分成m块
平均查找长度：ASL=ASL折半查找+ASL顺序查找= $log_2$ (m+1) +（n/m+1）/2

4. 二叉排序树BST

    private static class BinaryTreeNode {
        int data;
        BinaryTree lchild;
        BinaryTree rchild;
    }

public class BinarySearchTree {

    public static BinaryTreeNode serachBinaryTree(BinaryTreeNode btn, int key) {
        if (btn == null) { // 树节点不存在，返回
            return new BinaryTreeNode();
        } else if (key == btn.data) { // 查找成功
            return btn;
        } else if (key < btn.data) { // 关键字小于根节点查找左子树
            return serachBinaryTree(btn.lchild, key);
        } else { // 关键字大于根节点查找右子树
            return serachBinaryTree(btn.rchild, key);
        }
    }
}

时间复杂度：O(logn)
空间复杂度：O(1)
平均查找长度ASL：查找成功的平均查找长度、查找失败的平均查找长度

5. 哈希表查找

常用的哈希函数

直接地址法：H(key)=key或H(key)=a*key+b
除留余数法：H(key)= key mod p
数字分析法：可选取关键字的若干数位组成哈希地址，原则是使得到的哈希地址尽量避免冲突。
平方取中法：取关键字平方后的中间几位为哈希地址
常用的处理冲突方法
开发地址法：有线性探查法和平方探查法
链式地址法：把所有的同义词用单链表链接起来的方法，种方哈希表中每个单元中存放的不再是记录本身，而是相应同义词单链表的头指针。

时间复杂度：O(1)
空间复杂度：O(n)

二、排序

注意：下标都是从1开始的

1. 不带哨兵的直接插入排序

public void InsertSort(int nums[]){
	int temp;
	for(int i=2; i<nums.length; i++){
		temp = nums[i];
		int j = i;
		while(nums[j]<nums[j-1] && j > 1){
			nums[j] = nums[j-1];
		}
		nums[j+1] = temp;
	}
}

时间复杂度：最差时间复杂度O(n²)、平均时间复杂度O(n²)
空间复杂度：O(1)
稳定性：稳定

2. 带哨兵的直接插入排序

public void InsertSort(int nums[]){
	for(int i=2; i<nums.length; i++){
		nums[0] = nums[i];
		int j = i;
		while(nums[j]<nums[j-1]){
			nums[j] = nums[j-1];
		}
		nums[j+1] = nums[0];
	}
}

时间复杂度：最差时间复杂度O(n²)、平均时间复杂度O(n²)
空间复杂度：O(1)
稳定性：稳定

3. 带哨兵、折半查找的直接插入排序

折半查找跟顺序查找的效率都是一样的，因为将元素向后退的次数是一样的。

public void InsertSort(int nums[]){
	int low,high,mid;
	for(int i=2;i<=n;i++){
		A[0]=A[i];
		low=1;high=i-1;
		while(low<=high){
			mid=(low+high)/2;
			if(A[mid]>A[0]) high=mid-1;			//可用A[0]，也可用A[i]
			else low=mid+1
		}
		for(int j=i-1;j>=high+1;--j)	//注意这里只能用high，不能用low，mid
			A[j+1]=A[j];
		A[high+1]=A[0];
	}
}

时间复杂度：最差时间复杂度O(n²)、平均时间复杂度O(n²)
空间复杂度：O(1)
稳定性：稳定

4. 希尔排序

先追求表中元素的部分有序，再逐渐逼近全局有序。

public void ShellSort(int arr[], int gap){
	while(gap>=1){
		for(int i=0; i<gap; i++){
			for(int j=i+gapl j<arr.length; j+=gap){
				int temp = arr[i];
				for(int k = j-gap; k>=i&&arr[k]>temp; k-=gap){
						arr[k+gap] = arr[k];
				}
				arr[k+gap] = temp;
			}
		}
	}
}

时间复杂度：O(n^1.3~2)
空间复杂度：O(1)
稳定性：不稳定

5. 冒泡排序

public static void BubbleSort(int nums[]){
	for(int i = 1; i< nums.length; i++){
		boolean flag = true;
		for(int j = 0; j<nums.length-i; j++){
			if(arr[j] > arr[j+1]){
				int temp = arr[j];
				arr[j] = arr[j+1];
				arr[j+1] = temp;

				flag = false;
			}
		}
		if(flag) break;
	}
}

时间复杂度：最坏时间复杂度O(n²)、平均时间复杂度O(n²)
空间复杂度：O(1)
稳定性：稳定

6. 快速排序

public void quickSort(int[] nums, int left, int right){
	
	while(left >= right) return;
	
	int pivot = a[left];
	int i=left;
	int j=right;

	while(i < j){
		while(pivot <= a[j] && i<j) j--;
		while(pivot >= a[i] && i<j) i++;

		int temp = a[i];
		a[i] = a[j];
		a[j] = temp;
	}

	a[left] = a[i];
	a[i] = pivot;
   	
   	quickSort(a,left,i-1);//对左边的子数组进行快速排序
   	quickSort(a,i+1,right);//对右边的子数组进行快速排序
}

时间复杂度：最差时间复杂度O(n²)、平均时间复杂度O(n²)
空间复杂度：O(log₂n)~O(n)
稳定性：不稳定

7. 选择排序

public void SelectSort(int[] nums){
	for(int i=0; i<nums.length; i++){
		int temp = i;
		for(int j=i+1; j<nums.length; j++){
			if(nums[j] < nums[temp]) temp = j;
		}
		int swap = nums[i];
		nums[i] = nums[temp];
		nums[temp] = swap;
	}
}

时间复杂度：最差时间复杂度O(n²)、平均时间复杂度O(n²)
空间复杂度：O(1)
稳定性：稳定

8. 堆排序

堆排序分为两个过程：输出堆顶、调整新堆

void HeadAdjust(int A[],int k,int len){		//调整指定根节点A[k]
	A[0]=A[k];
	for(int i=k*2;i<=len;i*=2){
		if(i<len&&A[i]<A[i+1]) i++;		//不管要不要交换，先选出最大的子结点
		if(A[0]>=A[i]) break;		//不用交换，而且后面是一定调整好的了
		else{
			A[k]=A[i]
			k=i;			//这里与A[K]=A[0]相呼应，其实也可以选择A[i]=A[0]，每次都交换
		}
	}
	A[k]=A[0];
}

void BuildMaxHeap(int A[],int len){	//从最后一个子树根节点开始调整，调整全部根节点
	for(int i=len/2;i>0;--i)			
		HeadAdjust(A,i,len);
}

void HeapSort(int A[],int len){
	BuildMaxHeap(A,len);			//堆初始化
	
	for(i=len;i>1;i--){				
		Swap(A[i],A[1]);			//将最大值放在最后，然后重新在指定位置调整
		HeapAdjuest(A,1,i-1)		//截断最后一位，并且重新从第一位调整
	}
}

时间复杂度：最差时间复杂度O(nlog₂n)、平均时间复杂度O(nlog₂n)
空间复杂度：O(1)
稳定性：不稳定

9. 归并排序

把两个或多个已经有序的序列合并成一个

public static int[] sort(int[] a,int low,int high){
        int mid = (low+high)/2;
        if(low<high){
            sort(a,low,mid);
            sort(a,mid+1,high);
            //左右归并
            merge(a,low,mid,high);
        }
        return a;
    }
     
    public static void merge(int[] a, int low, int mid, int high) {
        int[] temp = new int[high-low+1];
        int i= low;
        int j = mid+1;
        int k=0;
        // 把较小的数先移到新数组中
        while(i<=mid && j<=high){
            if(a[i]<a[j]){
                temp[k++] = a[i++];
            }else{
                temp[k++] = a[j++];
            }
        }
        // 把左边剩余的数移入数组 
        while(i<=mid){
            temp[k++] = a[i++];
        }
        // 把右边边剩余的数移入数组
        while(j<=high){
            temp[k++] = a[j++];
        }
        // 把新数组中的数覆盖nums数组
        for(int x=0;x<temp.length;x++){
            a[x+low] = temp[x];
        }
    }

时间复杂度：最差时间复杂度O(nlog₂n)、平均时间复杂度O(nlog₂n)
空间复杂度：O(n)
稳定性：稳定

二叉树

1. 递归先序遍历

public static void preOrder(TreeNode root){
	if(root == null) return;
	
	System.out.println(root.value);
	if(root.left != null) PreOrder(root.left);
	if(root.right != null) PreOrder(root.right);
}

2. 非递归先序遍历

public static void preOrder(TreeNode root){
	Stack<TreeNode> stack = new Stack<TreeNode>();
	while(root != null || !stack.isEmpty()){
		while(root!=null){							// 1. 下去的时候
			System.out.println(root.value);		// 访问
			stack.push(root);					// 入栈
			root = root.left					// 左孩子
		}
		if(!stack.isEmpty()){		// 2. 回来的时候
			root = stack.pop();					// 出栈
			root = root.right;					// 右孩子
		}
	}
}

3. 递归中序遍历

public static void midOrder(TreeNode root){
	if(root == null) return;
	
	if(root.left != null) PreOrder(root.left);
	System.out.println(root.value);
	if(root.right != null) PreOrder(root.right);
}

4. 非递归中序遍历

public static void minOrder(TreeNode root){
	Stack<TreeNode> stack = new Stack<TreeNode>();
	while(root != null || !stack.isEmpty()){
		while(root!=null){							// 1. 下去的时候
			stack.push(root);					// 入栈
			root = root.left					// 左孩子
		}
		if(!stack.isEmpty()){		// 2. 回来的时候
			root = stack.pop();					// 出栈
			System.out.println(root.value);		// 访问
			root = root.right;					// 右孩子
		}
	}
}

5. 递归后序遍历

public static void postOrder(TreeNode root){
	if(root == null) return;
	
	if(root.left != null) PreOrder(root.left);
	if(root.right != null) PreOrder(root.right);
	System.out.println(root.value);
}

6. 非递归后序遍历

public void postorderTraversal(TreeNode root) {
    Deque<TreeNode> stack = new LinkedList<TreeNode>();
	TreeNode prev = null;			// prev是指上一个遍历到的结点
    
    if (root == null) return res;

    while (root != null || !stack.isEmpty()) {
        while (root != null) {
            stack.push(root);
            root = root.left;
        }
        root = stack.pop();

		// 要是没有右孩子，或者右孩子已经看过了，就打印根结点
        if (root.right == null || root.right == prev) {
            System.out.println(root.value);
            prev = root;		// 保留最近遍历过的一次结点
            root = null;		//这里设为null，就是好好的把结点输出
        } 
        // 右孩子不是空的，并且上次prev没有走过的，就push进栈。
        else{	 
			stack.push(root);
            root = root.right;
		}
    }
}

7. 广度遍历二叉树

public  static void bfs(TreeNode root){
	Queue<TreeNode> queue = new LinkedList<TreeNode>();

	if(root == null) return;
	queue.add(root);
	
	while(!queue.isEmpty()){
		TreeNode t = queue.remove();
		System.out.println(root.value);	
		if(t.left != null) queue.add(t.left);
		if(t.right != null) queue.add(t.right);
	}
}

8. 深度遍历

    public void dfs(TreeNode root){
        Stack<TreeNode> stack=new Stack<TreeNode>();
 
        if(root==null)
            return list;
	    
	    //压入根节点
        stack.push(root);
    	
    	//然后就循环取出和压入节点，直到栈为空，结束循环
        while (!stack.isEmpty()){
            TreeNode t=stack.pop();
            if(t.right!=null)
                stack.push(t.right);
            if(t.left!=null)
                stack.push(t.left);
            System.out.println(t.value);
        }
}