剑指 Offer day5， day6

二分查找和二叉树的题目

剑指 Offer 04. 二维数组中的查找

剑指 Offer 04. 二维数组中的查找 - 力扣（Leetcode）

依然是利用特殊的数据状况改进查找的速度，注意边界条件。

题解这个类比二叉树的思路非常巧妙。不过是从左下到右上。

解题思路：

若使用暴力法遍历矩阵 matrix ，则时间复杂度为 O(NM) 。暴力法未利用矩阵 “从上到下递增、从左到右递增” 的特点，显然不是最优解法。

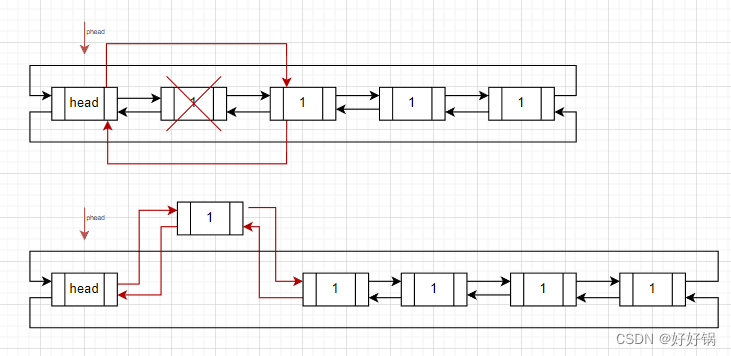
如下图所示，我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于 二叉搜索树 ，即对于每个元素，其左分支元素更小、右分支元素更大。因此，通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素，本文称之为 标志数 ，以 matrix 中的 左下角元素 为标志数 flag ，则有:

1. 若 flag > target ，则 target 一定在 flag 所在 行的上方 ，即 flag 所在行可被消去。

2. 若 flag < target ，则 target 一定在 flag 所在 列的右方 ，即 flag 所在列可被消去。

算法流程：

1. 从矩阵 matrix 左下角元素（索引设为 (i, j) ）开始遍历，并与目标值对比：
   当 matrix[i][j] > target 时，执行 i-- ，即消去第 i 行元素；
   当 matrix[i][j] < target 时，执行 j++ ，即消去第 j 列元素；
   当 matrix[i][j] = target 时，返回 true ，代表找到目标值。

2. 若行索引或列索引越界，则代表矩阵中无目标值，返回 false 。

   每轮 i 或 j 移动后，相当于生成了“消去一行（列）的新矩阵”， 索引(i,j) 指向新矩阵的左下角元素（标志数），因此可重复使用以上性质消去行（列）。

复杂度分析：
时间复杂度 O(M+N) ：其中，N 和 M 分别为矩阵行数和列数，此算法最多循环 M+N 次。
空间复杂度 O(1) : i, j 指针使用常数大小额外空间。

class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if(matrix.size() < 1 || matrix[0].size() < 1) {
            return false;
        }
        if(matrix[0][0] > target || matrix[matrix.size()-1][matrix[0].size()-1] < target){
            return false;
        }
        int top = 0, left = matrix[0].size()-1;
        while(left >= 0 && top < matrix.size()){
            if(matrix[top][left] > target){
                left--;
            } else if(matrix[top][left] < target){
                top++;
            } else{
                return true;
            }
        }
        return false;
    }
};

剑指 Offer 11. 旋转数组的最小数字

剑指 Offer 11. 旋转数组的最小数字 - 力扣（Leetcode）

依旧是有序数组，所以注意二分法的使用。重点是中点等于右侧值的时候边界的变化。

解题思路：

如下图所示，寻找旋转数组的最小元素即为寻找 右排序数组 的首个元素 nums[x] ，称 x 为 旋转点 。

排序数组的查找问题首先考虑使用 二分法 解决，其可将 遍历法 的 线性级别 时间复杂度降低至 对数级别 。

算法流程：

1. 初始化： 声明 i, j 双指针分别指向 nums 数组左右两端；
2. 循环二分： 设 m=(i+j)/2 为每次二分的中点（ “/” 代表向下取整除法，因此恒有 i≤m<j），可分为以下三种情况：
   a. 当 nums[m]>nums[j] 时： m 一定在 左排序数组 中，即旋转点 x一定在 [m+1,j] 闭区间内，因此执行 i=m+1；
   b. 当 nums[m]<nums[j] 时： m 一定在 右排序数组 中，即旋转点 x一定在[i,m] 闭区间内，因此执行 j=m；
   c. 当 nums[m]=nums[j] 时： 无法判断 m 在哪个排序数组中，即无法判断旋转点 x在 [i,m] 还是 [m+1,j] 区间中。解决方案： 执行 j=j−1 缩小判断范围，分析见下文。
3. 返回值： 当 i=j 时跳出二分循环，并返回 旋转点的值 nums[i] 即可。

复杂度分析：

• 时间复杂度 O(log⁡2N)： 在特例情况下（例如 [1,1,1,1]），会退化到 O(N)。时间复杂度 O(log⁡2N)

• 空间复杂度 O(1) ： i, j, m 变量使用常数大小的额外空间。

class Solution {
public:
    int minArray(vector<int>& numbers) {
        int left = 0, right = numbers.size() - 1;
        while(left < right){
            int mid = left + (right - left) / 2;
            if(numbers[mid] > numbers[right]){
                left = mid + 1;
            } else if(numbers[mid] < numbers[right]){
                right = mid;
            } else{
                right--;
            }
        }
        return numbers[left]; 
    }
};

剑指 Offer 50. 第一个只出现一次的字符

剑指 Offer 50. 第一个只出现一次的字符 - 力扣（Leetcode）

哈希表的运用。

本题考察 哈希表 的使用，本文介绍 哈希表 和 有序哈希表 两种解法。其中，在字符串长度较大、重复字符很多时，“有序哈希表” 解法理论上效率更高。

方法一：哈希表

1. 遍历字符串 s ，使用哈希表统计 “各字符数量是否 >1 ”。
2. 再遍历字符串 s ，在哈希表中找到首个 “数量为 1 的字符”，并返回。

算法流程：

1. 初始化： 字典 (Python)、HashMap(Java)、map(C++)，记为 dic ；
2. 字符统计： 遍历字符串 s 中的每个字符 c ；
   a. 若 dic 中 不包含 键(key) c ：则向 dic 中添加键值对 (c, True) ，代表字符 c 的数量为 1 ；
   b. 若 dic 中 包含 键(key) c ：则修改键 c 的键值对为 (c, False) ，代表字符 c 的数量 >1 。
3. 查找数量为 1 的字符： 遍历字符串 s 中的每个字符 c ；
   a. 若 dic中键 c 对应的值为 True ：，则返回 c 。
4. 返回 ’ ’ ，代表字符串无数量为 1 的字符。

复杂度分析：
时间复杂度 O(N) ： N 为字符串 s 的长度；需遍历 s 两轮，使用 O(N) ；HashMap 查找操作的复杂度为 O(1)；
空间复杂度 O(1) ： 由于题目指出 s 只包含小写字母，因此最多有 26 个不同字符，HashMap 存储需占用 O(26)=O(1) 的额外空间。

方法二：有序哈希表

方法二：有序哈希表
在哈希表的基础上，有序哈希表中的键值对是 按照插入顺序排序 的。基于此，可通过遍历有序哈希表，实现搜索首个 “数量为 1 的字符”。

哈希表是 去重 的，即哈希表中键值对数量 ≤ 字符串 s 的长度。因此，相比于方法一，方法二减少了第二轮遍历的循环次数。当字符串很长（重复字符很多）时，方法二则效率更高。

复杂度分析：
时间和空间复杂度均与 “方法一” 相同，而具体分析：方法一 需遍历 s 两轮；方法二 遍历 s 一轮，遍历 dic 一轮（ dic 的长度不大于 26 ）。

剑指 Offer 32 - I. 从上到下打印二叉树

剑指 Offer 32 - I. 从上到下打印二叉树 - 力扣（Leetcode）

二叉树的层序遍历，使用队列来完成。

解题思路：

• 题目要求的二叉树的 从上至下 打印（即按层打印），又称为二叉树的 广度优先搜索（BFS）。
• BFS 通常借助 队列 的先入先出特性来实现。

算法流程：

1. 特例处理： 当树的根节点为空，则直接返回空列表 [] ；
2. 初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] ；
3. BFS 循环： 当队列 queue 为空时跳出；
   a. 出队： 队首元素出队，记为 node；
   b. 打印： 将 node.val 添加至列表 tmp 尾部；
   c. 添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
4. 返回值： 返回打印结果列表 res 即可。

复杂度分析：
时间复杂度 O(N) ： N 为二叉树的节点数量，即 BFS 需循环 N 次。
空间复杂度 O(N) ： 最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 O(N) 大小的额外空间。

这种方式需要注意当前层的size是不能变的，要先记录下来。

class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        if(root == NULL){return {};}
        queue<TreeNode*> que;
        vector<int> result;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i = 0; i < size; i++){
                TreeNode* cur = que.front();
                result.push_back(cur->val);
                que.pop();
                if(cur->left != NULL){que.push(cur->left);}
                if(cur->right != NULL){que.push(cur->right);}
            }
        }
        return result;
    }
};

还有直接添加的方式：

class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        vector<int> res;
        if(!root)
            return res;
        queue<TreeNode*> q;
        q.push(root);
        while(q.size()){
            TreeNode* node=q.front();
            q.pop();
            res.push_back(node->val);
            if(node->left)
                q.push(node->left);
            if(node->right)
                q.push(node->right);
        }
        return res;

    }
};

剑指 Offer 32 - II. 从上到下打印二叉树 II

剑指 Offer 32 - II. 从上到下打印二叉树 II - 力扣（Leetcode）

每一次记录完了再记录层序，思路和初级版本类似，收集结果的位置不同而已。

解题思路：

建议先做 面试题32 - I. 从上到下打印二叉树 再做此题，两题仅有微小区别，即本题需将 每一层打印到一行 。

I. 按层打印： 题目要求的二叉树的 从上至下 打印（即按层打印），又称为二叉树的 广度优先搜索（BFS）。BFS 通常借助 队列 的先入先出特性来实现。

II. 每层打印到一行： 将本层全部节点打印到一行，并将下一层全部节点加入队列，以此类推，即可分为多行打印。

算法流程：

1. 特例处理： 当根节点为空，则返回空列表 [] ；
2. 初始化： 打印结果列表 res = [] ，包含根节点的队列 queue = [root] ；
3. BFS 循环： 当队列 queue 为空时跳出；
   a. 新建一个临时列表 tmp ，用于存储当前层打印结果；
   b. 当前层打印循环： 循环次数为当前层节点数（即队列 queue 长度）；
   1. 出队： 队首元素出队，记为 node；
   2. 打印： 将 node.val 添加至 tmp 尾部；
   3. 添加子节点： 若 node 的左（右）子节点不为空，则将左（右）子节点加入队列 queue ；
      c. 将当前层结果 tmp 添加入 res 。
4. 返回值： 返回打印结果列表 res 即可。

复杂度分析：
时间复杂度 O(N) ： N 为二叉树的节点数量，即 BFS 需循环 N 次。
空间复杂度 O(N) ： 最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 O(N) 大小的额外空间。

剑指 Offer 32 - III. 从上到下打印二叉树 III

剑指 Offer 32 - III. 从上到下打印二叉树 III - 力扣（Leetcode）

利用了双端队列的性质，减少了额外的储存空间和逆转数组等操作。

解题思路：

方法一：层序遍历 + 双端队列

• 利用双端队列的两端皆可添加元素的特性，设打印列表（双端队列） tmp ，并规定：
  奇数层 则添加至 tmp 尾部 ，
  偶数层 则添加至 tmp 头部 。

算法流程：

1. 特例处理： 当树的根节点为空，则直接返回空列表 [] ；
2. 初始化： 打印结果空列表 res ，包含根节点的双端队列 deque ；
3. BFS 循环： 当 deque 为空时跳出；
   1. 新建列表 tmp ，用于临时存储当前层打印结果；
   2. 当前层打印循环： 循环次数为当前层节点数（即 deque 长度）；
      1. 出队： 队首元素出队，记为 node；
      2. 打印： 若为奇数层，将 node.val 添加至 tmp 尾部；否则，添加至 tmp 头部；
      3. 添加子节点： 若 node 的左（右）子节点不为空，则加入 deque ；
   3. 将当前层结果 tmp 转化为 list 并添加入 res ；
4. 返回值： 返回打印结果列表 res 即可；

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()) {
            LinkedList<Integer> tmp = new LinkedList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                if(res.size() % 2 == 0) tmp.addLast(node.val); // 偶数层 -> 队列头部
                else tmp.addFirst(node.val); // 奇数层 -> 队列尾部
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            res.add(tmp);
        }
        return res;
    }
}

方法二：层序遍历 + 双端队列（奇偶层逻辑分离）

方法一代码简短、容易实现；但需要判断每个节点的所在层奇偶性，即冗余了 NNN 次判断。
通过将奇偶层逻辑拆分，可以消除冗余的判断。

算法流程：

与方法一对比，仅 BFS 循环不同。

• BFS 循环： 循环打印奇 / 偶数层，当 deque 为空时跳出；
  1. 打印奇数层： 从左向右 打印，先左后右 加入下层节点；
  2. 若 deque 为空，说明向下无偶数层，则跳出；
  3. 打印偶数层： 从右向左 打印，先右后左 加入下层节点；

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) deque.add(root);
        while(!deque.isEmpty()) {
            // 打印奇数层
            List<Integer> tmp = new ArrayList<>();
            for(int i = deque.size(); i > 0; i--) {
                // 从左向右打印
                TreeNode node = deque.removeFirst();
                tmp.add(node.val);
                // 先左后右加入下层节点
                if(node.left != null) deque.addLast(node.left);
                if(node.right != null) deque.addLast(node.right);
            }
            res.add(tmp);
            if(deque.isEmpty()) break; // 若为空则提前跳出
            // 打印偶数层
            tmp = new ArrayList<>();
            for(int i = deque.size(); i > 0; i--) {
                // 从右向左打印
                TreeNode node = deque.removeLast();
                tmp.add(node.val);
                // 先右后左加入下层节点
                if(node.right != null) deque.addFirst(node.right);
                if(node.left != null) deque.addFirst(node.left);
            }
            res.add(tmp);
        }
        return res;
    }
}

方法三：层序遍历 + 倒序

• 此方法的优点是只用列表即可，无需其他数据结构。
• 偶数层倒序： 若 res 的长度为 奇数 ，说明当前是偶数层，则对 tmp 执行 倒序 操作。

复杂度分析：
时间复杂度 O(N) ： NNN 为二叉树的节点数量，即 BFS 需循环 N 次，占用 O(N) 。共完成 少于 N 个节点的倒序操作，占用 O(N) 。
空间复杂度 O(N) ： 最差情况下，即当树为满二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 O(N) 大小的额外空间。

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<List<Integer>> res = new ArrayList<>();
        if(root != null) queue.add(root);
        while(!queue.isEmpty()) {
            List<Integer> tmp = new ArrayList<>();
            for(int i = queue.size(); i > 0; i--) {
                TreeNode node = queue.poll();
                tmp.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            if(res.size() % 2 == 1) Collections.reverse(tmp);
            res.add(tmp);
        }
        return res;
    }
}