NumPy 简单入门基础
我的另一篇文章 : Numpy介绍-深度学习:Numpy介绍-深度学习(Numpy介绍深度学习使用看这些足够了)
import numpy as np
my_array = np.array([1, 2, 3, 4, 5])
print(my_array)
[1 2 3 4 5]
print(my_array.shape)
(5,)
数组基础
创建一个数组
NumPy围绕这些称为数组的事物展开。实际上它被称之为 ndarrays,你不知道没事儿。使用NumPy提供的这些数组,我们就可以以闪电般的速度执行各种有用的操作,如矢量和矩阵、线性代数等数学运算!(开个玩笑,本文章中我们不会做任何繁重的数学运算)
a = np.array([0, 1, 2, 3, 4, 5])
b = np.array((0, 1, 2, 3, 4, 5))
c = np.arange(6)
d = np.linspace(0, 2 * np.pi, 6)
print(a)
print(b)
print(c)
print(d)
[0 1 2 3 4 5]
[0 1 2 3 4 5]
[0 1 2 3 4 5]
[0. 1.25663706 2.51327412 3.76991118 5.02654825 6.28318531]
a = np.array(
[
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35],
]
)
print(a[2, 4])
25
数组切片
# MD slicing
print(a[0, 1:4]) # >>>[12 13 14]
print(a[1:4, 0]) # >>>[16 21 26]
print(a[::2, ::2])
# >>>[[11 13 15]
# [21 23 25]
# [31 33 35]]
print(a[:, 1]) # >>>[12 17 22 27 32]
[12 13 14]
[16 21 26]
[[11 13 15]
[21 23 25]
[31 33 35]]
[12 17 22 27 32]
多维数组切片
# MD Array,
a = np.array(
[
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35],
]
)
print(a[2, 4]) # >>>25
# MD slicing
print(a[0, 1:4]) # >>>[12 13 14]
print(a[1:4, 0]) # >>>[16 21 26]
print(a[::2, ::2]) # >>>[[11 13 15]
# [21 23 25]
# [31 33 35]]
print(a[:, 1]) # >>>[12 17 22 27 32]
25
[12 13 14]
[16 21 26]
[[11 13 15]
[21 23 25]
[31 33 35]]
[12 17 22 27 32]
如你所见,通过对每个以逗号分隔的维度执行单独的切片,你可以对多维数组进行切片。因此,对于2D数组,我们的第一片定义了行的切片,第二片定义了列的切片。
注意,只需输入数字就可以指定行或列。上面的第一个示例从数组中选择第0列。
下面的图表说明了给定的示例切片是如何进行工作的。
numpy数组切片工作原理:
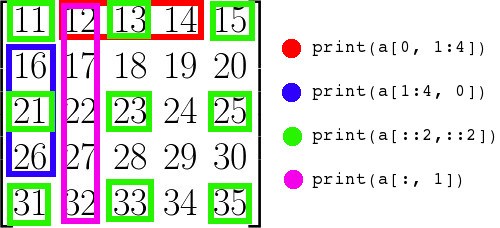
数组属性
# Array properties
a = np.array(
[
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35],
]
)
print(type(a)) # >>><class 'numpy.ndarray'>
print(a.dtype) # >>>int64
print(a.size) # >>>25
print(a.shape) # >>>(5, 5)
print(a.itemsize) # >>>8
print(a.ndim) # >>>2
print(a.nbytes) # >>>200
<class 'numpy.ndarray'>
int32
25
(5, 5)
4
2
100
正如你在上面的代码中看到的,NumPy数组实际上被称为ndarray。我不知道为什么他妈的它叫ndarray,如果有人知道请留言!我猜它代表n维数组。
数组的形状是它有多少行和列,上面的数组有5行和5列,所以它的形状是(5,5)。
itemsize属性是每个项占用的字节数。这个数组的数据类型是int 32,一个int 32中有32位,一个字节中有8位,除以32除以8,你就可以得到它占用了多少字节,在本例中是8。
ndim 属性是数组的维数。这个有2个。例如,向量只有1。
nbytes 属性是数组中的所有数据消耗掉的字节数。你应该注意到,这并不计算数组的开销,因此数组占用的实际空间将稍微大一点。
使用数组
基本操作符
只是能够从数组中创建和检索元素和属性不能满足你的需求,你有时也需要对它们进行数学运算。 你完全可以使用四则运算符 +、- 、/ 来完成运算操作。
# Basic Operators
a = np.arange(25)
a = a.reshape((5, 5))
b = np.array(
[
10,
62,
1,
14,
2,
56,
79,
2,
1,
45,
4,
92,
5,
55,
63,
43,
35,
6,
53,
24,
56,
3,
56,
44,
78,
]
)
b = b.reshape((5, 5))
print(a + b)
print(a - b)
print(a * b)
print(a / b)
print(a**2)
print(a < b)
print(a > b)
print(a.dot(b))
[[ 10 63 3 17 6]
[ 61 85 9 9 54]
[ 14 103 17 68 77]
[ 58 51 23 71 43]
[ 76 24 78 67 102]]
[[-10 -61 1 -11 2]
[-51 -73 5 7 -36]
[ 6 -81 7 -42 -49]
[-28 -19 11 -35 -5]
[-36 18 -34 -21 -54]]
[[ 0 62 2 42 8]
[ 280 474 14 8 405]
[ 40 1012 60 715 882]
[ 645 560 102 954 456]
[1120 63 1232 1012 1872]]
[[0. 0.01612903 2. 0.21428571 2. ]
[0.08928571 0.07594937 3.5 8. 0.2 ]
[2.5 0.11956522 2.4 0.23636364 0.22222222]
[0.34883721 0.45714286 2.83333333 0.33962264 0.79166667]
[0.35714286 7. 0.39285714 0.52272727 0.30769231]]
[[ 0 1 4 9 16]
[ 25 36 49 64 81]
[100 121 144 169 196]
[225 256 289 324 361]
[400 441 484 529 576]]
[[ True True False True False]
[ True True False False True]
[False True False True True]
[ True True False True True]
[ True False True True True]]
[[False False True False True]
[False False True True False]
[ True False True False False]
[False False True False False]
[False True False False False]]
[[ 417 380 254 446 555]
[1262 1735 604 1281 1615]
[2107 3090 954 2116 2675]
[2952 4445 1304 2951 3735]
[3797 5800 1654 3786 4795]]
数组特殊运算符
NumPy还提供了一些别的用于处理数组的好用的运算符。
# dot, sum, min, max, cumsum
a = np.arange(10)
print(a.sum()) # >>>45
print(a.min()) # >>>0
print(a.max()) # >>>9
print(a.cumsum()) # >>>[ 0 1 3 6 10 15 21 28 36 45]
45
0
9
[ 0 1 3 6 10 15 21 28 36 45]
sum()、min()和max()函数的作用非常明显。将所有元素相加,找出最小和最大元素。
然而,cumsum()函数就不那么明显了。它将像sum()这样的每个元素相加,但是它首先将第一个元素和第二个元素相加,并将计算结果存储在一个列表中,然后将该结果添加到第三个元素中,然后再将该结果存储在一个列表中。这将对数组中的所有元素执行此操作,并返回作为列表的数组之和的运行总数。
进阶索引
花式索引
花式索引是获取数组中我们想要的特定元素的有效方法。
# Fancy indexing
a = np.arange(0, 100, 10)
indices = [1, 5, -1]
b = a[indices]
print(a) # >>>[ 0 10 20 30 40 50 60 70 80 90]
print(b) # >>>[10 50 90]
[ 0 10 20 30 40 50 60 70 80 90]
[10 50 90]
整数数组索引
使用切片索引到numpy数组时,生成的数组视图将始终是原始数组的子数组。 相反,整数数组索引允许你使用另一个数组中的数据构造任意数组。 这是一个例子:
import numpy as np
a = np.array([[1, 2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
[1 4 5]
[1 4 5]
[2 2]
[2 2]
正如你在上面的示例中所看到的,我们使用我们想要检索的特定索引序列对数组进行索引。这反过来返回我们索引的元素的列表。
布尔屏蔽
布尔屏蔽是一个有用的功能,它允许我们根据我们指定的条件检索数组中的元素。
# Boolean masking
import matplotlib.pyplot as plt
a = np.linspace(0, 2 * np.pi, 50)
b = np.sin(a)
plt.plot(a, b)
mask = b >= 0
plt.plot(a[mask], b[mask], "bo")
mask = (b >= 0) & (a <= np.pi / 2)
plt.plot(a[mask], b[mask], "go")
plt.show()
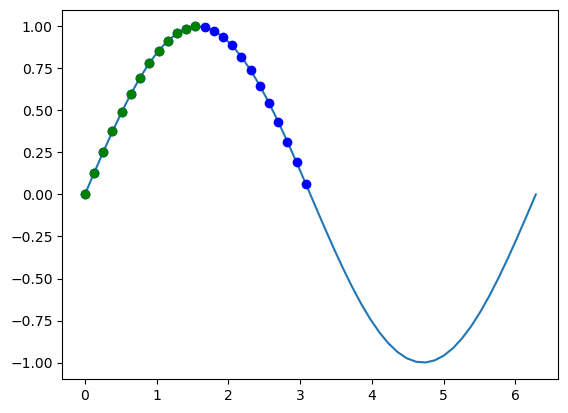
上面的示例显示了如何进行布尔屏蔽。 你所要做的就是将数组传递给涉及数组的条件,它将为你提供一个值的数组,为该条件返回true。
缺省索引
不完全索引是从多维数组的第一个维度获取索引或切片的一种方便方法。 例如,如果数组a=[1,2,3,4,5],[6,7,8,9,10],那么[3]将在数组的第一个维度中给出索引为3的元素,这里是值4。
# Incomplete Indexing
a = np.arange(0, 100, 10)
b = a[:5]
c = a[a >= 50]
print(b) # >>>[ 0 10 20 30 40]
print(c) # >>>[50 60 70 80 90]
[ 0 10 20 30 40]
[50 60 70 80 90]
Where 函数
where() 函数是另外一个根据条件返回数组中的值的有效方法。 只需要把条件传递给它,它就会返回一个使得条件为真的元素的列表。
# Where
a = np.arange(0, 100, 10)
b = np.where(a < 50)
c = np.where(a >= 50)[0]
print(b) # >>>(array([0, 1, 2, 3, 4]),)
print(c) # >>>[5 6 7 8 9]
(array([0, 1, 2, 3, 4], dtype=int64),)
[5 6 7 8 9]