2019年第九届MathorCup高校数学建模挑战赛
B题 环形穿梭车系统的设计与调度
原题再现:


整体求解过程概述(摘要)
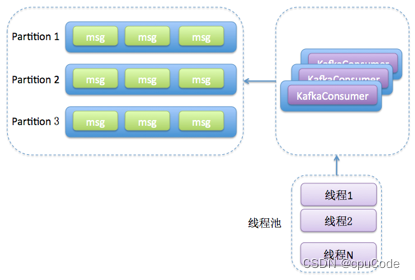
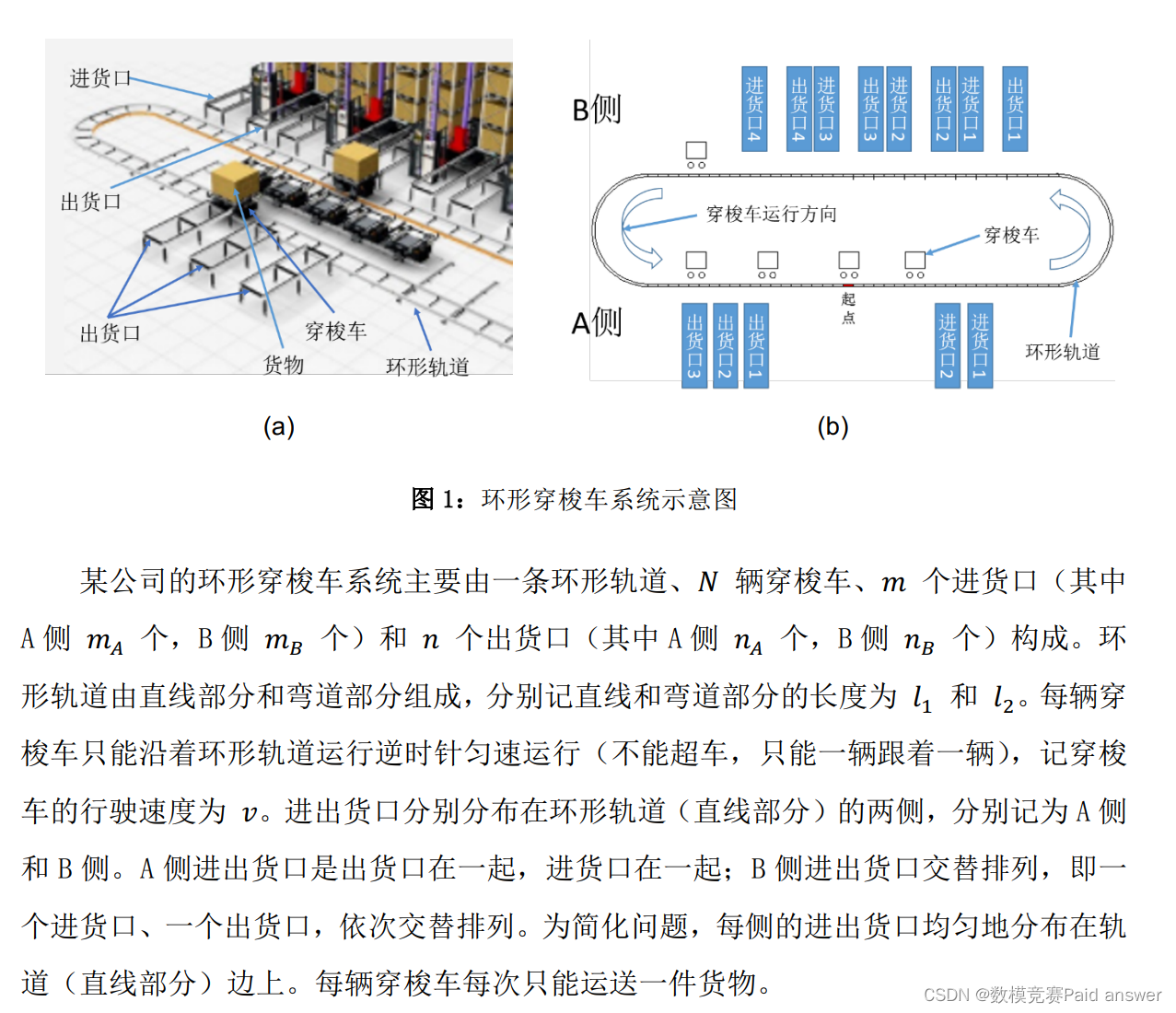
环形穿梭车系统为集多种高新技术于一体的自动搬运设备,行驶和输送速度快、灵活性好、自动化程度高。但由于系统采用封闭式轨道,不合理的系统参数设计及车辆调度会加剧轨道堵塞,降低运行效率。因此,本文对环形穿梭车系统的设计和调度进行深入研究,主要解决了如下若干问题:
问题 1,根据给定环形穿梭车系统约定及任务,将穿梭车看成质点,建立以总完工任务为目标函数的模型,约束条件为不可超车,穿梭车只能执行一个搬运任务及各参数取值范围限制等。利用自适应遗传算法对模型进行求解,算法初始种群由规则调度生成,加快收敛速度。对穿梭车数量 N=3,6,9 的情况分别求解模型得到完工时间Ttask为 10880s、6943s 以及 5805s,并对三种情况进行对比分析。
问题 2,基于问题 1 调度模型,考虑穿梭车长度,更改约束条件,穿梭车之间距离定义为从前车尾到后车头,安全距离lsafe=1.3m。对穿梭车数量 N=3,6,9 的情况分别求解模型得到完工时间Ttask分别为 11137s、7122s 以及 5843s,并对问题 1 与问题 2 六种情况作对比分析。
问题 3,根据问题 1 和问题 2 求得总拥堵时间、最大货物吞吐量、复合作业次数以及有效搬运总距离比四个穿梭车系统运行效率评价指标。分别采用层次分析法和熵值法进行初步指标权重选取,然后建立最小二乘主客观一致赋权评价模型,引入拉格朗日函数进行模型进行求解,构造正、负理想方案,得到问题 1 与问题 2 六种情况的最终评价系数 F 分别为:0.5191、0.5475、0.6337、0.4514、0.5761 以及 0.6226;系数越大,系统运行效率越高。
问题 4,从货物角度进行系统建模,引入排队理论,建立 M/M/n 排队模型。以轨道直线部分长度、弯道部分长度、穿梭车行驶速度和穿梭车数量作为系统待优化的参数,将系统服务强度,系统内所有穿梭车空闲概率、系统中平均等待队长和平均正在服务的穿梭车台数作为寻优目标函数;将模型转化多目标寻优问题,采用带约束的粒子群优化算法进行模型求解,得到参数优化结果,建议轨道直线部分长度为 113.5m,弯道部分长度为 7.1m,穿梭车速度为 1.2m/s,穿梭车数目为 6。
模型假设:
1、假设穿梭车无起停加减速时间,为立起立停,即也无最小制动距离等;
2、假设穿梭车位置检测时间、安全检测时间、通讯时间等常数定值时间可不计;
3、假设穿梭车、道口在整个调度运行周期中不发生故障等意外停止运行情况,或此情况对调度优化过程不产生影响。
问题分析:
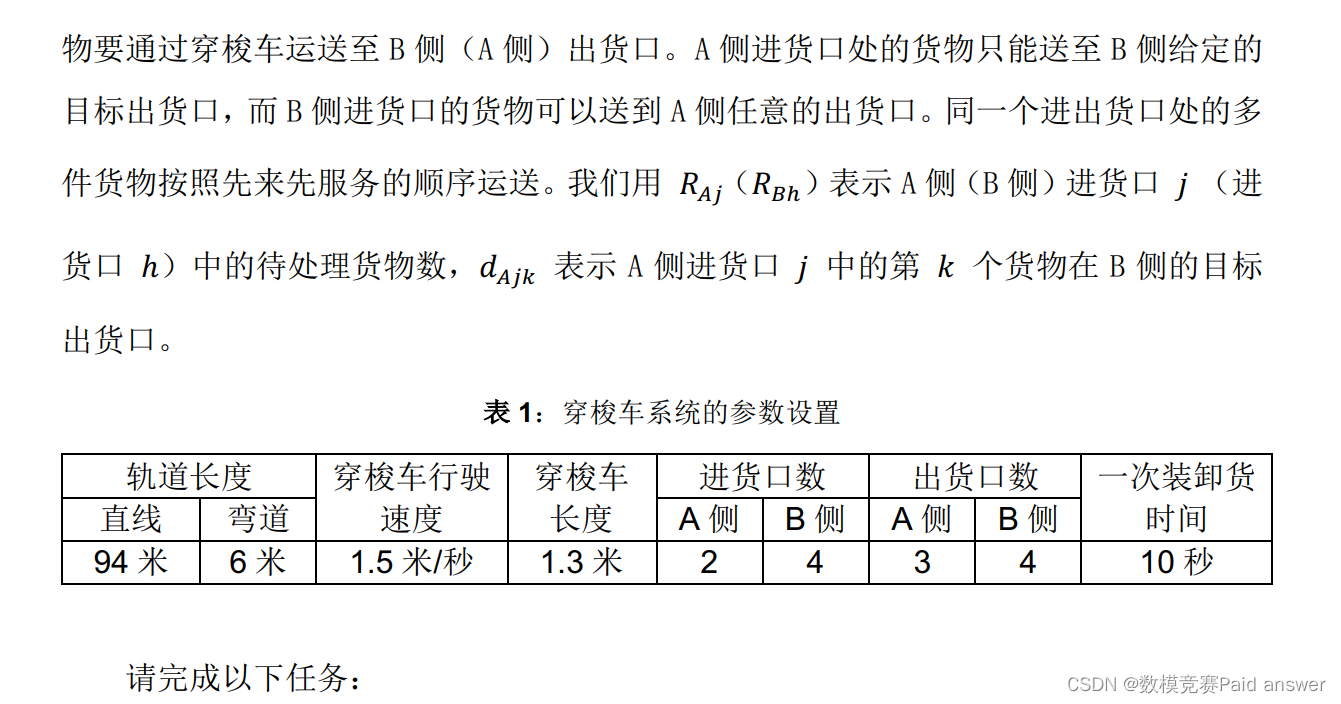
1.不计穿梭车实际长度,建立一般化的调度 N 辆穿梭车完成各个进货口待处理货物的数学模型和相应求解算法,目标为总完工时间最小。并根据表 1 给定系统参数,求解N=3,6,9 时,完成附件 1 附件 2 给定的待处理货物所需时间。
分析:该问题为车辆调度问题,需根据题目给定环形穿梭车系统描述,建立一般化调度模型,使系统在完成任务的基础上总完工时间最短。当不计穿梭车实际长度时,可将穿梭车看为质点。并将建立的调度模型用于实际应用,求解给定系统具体参数,穿梭车数量及任务时的总完工时间。
2.考虑穿梭车实际长度,建立一般化的调度 N 辆穿梭车完成各个进货口待处理货物的数学模型和相应求解算法,目标为总完工时间最小。并根据表 1 给定系统参数,求解N=3,6,9 时,完成附件 1 附件 2 给定的待处理货物所需时间。
分析:该问题大体思路与问题一类似,区别在于该问题不能将穿梭车看为质点,需考虑穿梭车本身长度对系统运行的影响。
3.根据表 1,附件 1 及附件 2 数据,对环形穿梭车系统运行效率进行评价。
分析:该问题为系统运行效率评价问题,先需找到系统评价指标,再对评价指标进行融合得到综合特征评价指标等,最后得到系统评价值。系统评价指标可从穿梭车拥堵时间,系统最大货物吞吐量等角度进行选取,评价指标融合方法有主观或客观多指标融合方法。
4.对此环形穿梭车系统进行参数优化设计,并给出实际可行改进建议。
分析:该问题为系统优化设计问题,首先需分析各参数对系统运行效率的影响,然后对参数值进行寻优,可用带约束的优化方法进行求解。最后根据求解值提出系统参数改进建议。
模型的建立与求解整体论文缩略图



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
The actual procedure is shown in the screenshot
基于遗传算法的穿梭车调度主函数
function [time]=GA()
N=3;num=10;%每次迭代一个口货物的数量,染色体携带的基因个数
popsize=20; %初始种群大小
Generationnmax=20; %最大代数
pcrossover=0.8; %交配概率
pmutation=0.1;%变异概率
fitness=zeros(1,popsize);%%产生初始种群,两个矩阵
A_2=xlsread('A.xlsx');A_2(:,1)=A_2(:,1)+A_2(:,2);A_2(:,2)=A_2(:,1)-A_2(:,2);
A_2(:,1)=A_2(:,1)-A_2(:,2);A_2_ini=A_2;
population=[ceil(4+3*rand(100,4,popsize)),ceil(N*rand(100,6,popsize))];
for i=1:popsize
population(52:100,2,i)=0;
population(72:100,3,i)=0;
population(52:100,8,i)=0;
population(72:100,9,i)=0;
end%%迭代的时候用到的 population 信息,ini 为所有信息,raise 随着迭代不断上升,
best 为最优种群
population_ini=population;population_raise=[];scnew=zeros(num,10,popsize);
smnew=zeros(num,10,popsize);handle_waitbar=waitbar(0,'Please wait...');%%每次迭代10个
货物
for s=1:10
start=10*s-9;
the_end=10*s;%%每次迭代取 ini 对应的 10 行,population_part 的值每次都在变
population_part_s=population_ini(start:the_end,:,:);
A_2_part=A_2_ini(1:the_end,:);Generation=0;
while Generation<Generationnmax
Generation=Generation+1;%%算 raise 后的适应度
for i=1:popsize
fitness(i)=simulation([population_raise;population_part_s(:,:,i)],A_2_part,N);
end%给适应度函数加上一个大小合理的数以便保证种群适应值为正数
fitness=fitness';
valuemax=max(fitness);
fitness=(valuemax-fitness);
fsum=sum(fitness);
Pperpopulation=fitness/fsum;
cumsump=cumsum(Pperpopulation);
cumsump=cumsump';%%只对 part 进行交叉等操作
for j=1:2:popsize %选择操作
seln=selection(cumsump); %交叉操作
scro=crossover(population_part_s,seln,pcrossover);
scnew(:,:,j)=scro(:,:,1);scnew(:,:,j+1)=scro(:,:,2);
smnew(:,:,j)=mutation(scnew(:,:,j),pmutation,N);
smnew(:,:,j+1)=mutation(scnew(:,:,j+1),pmutation,N);
end%产生了新的种群,part
population_part_s=smnew;
end%%计算 raise 后的适应度
for i=1:popsize
fitness(i)=simulation([population_raise();population_part_s(:,:,i)],A_2_part,N);
end
[~,index]=min(fitness); population_raise(start:the_end,:)=population_part_s(:,:,index);
waitbar(s/20,handle_waitbar)
end
close(handle_waitbar);time=simulation(population_raise,A_2_ini,N);
xlswrite('task.xlsx',population_raise);
end
环形穿梭车调度过程
function
[port_state,vehicle_state]=Fnc_update_state(task_assignment,task_information,port_state,veh
icle_state,vehicle_coordinate,in_coordinate,out_coordinate,N)
% vehicle_state 第一行代表 N 个运输车的状态,
%0 表示空闲%1 代表正在装货%2 代表正在运货%3 代表正在卸货
% 第二行代表货物来源于哪个进货口(编号 1-6),从开始装货到开始卸货此数值不为
0
% 第三行代表需要将货物送到哪个出货口(编号 1-7),从开始装货到开始卸货此数值
不为 0
% 第四行在运输车不处于 flag=1 或 3 时为 0,当 flag==1 或 3 时其数字代表装卸货剩余
的时间,本程序中由于取了 h=0.01
% 因为浮点数的判定条件问题所以取这个数字的范围为 0-100,每当进行一个 whlie 循
环 t 增加 0.1, 10s 对应 100 次循环
%%port_state 口的状态,列数为 6,6 个进货口
%%第一行代表每一个口下一个有待装箱的货物编号%%第二行代表这个货物由哪个运
输车负责%%第三行代表这个货物要送到哪个口
for i=1:N%%如果空闲则满足一定条件变成装货
if(vehicle_state(1,i)==0)
%%检测第 i 个车是否到达对应进货口,如果已经到达进货口则进行装箱,
%%并将小车状态改为正在装货,记录起始地和目的地,并将等待时间置 100.
%%0.15=0.1*1.5,代表进货出货区间
delta=vehicle_coordinate(i)-in_coordinate;%index 代表哪个进货口
index=find((0<delta)&(delta<=0.15));%有空闲的运输车到达进货口
if(~isempty(index))
if port_state(2,index)==i
vehicle_state(1,i)=1; vehicle_state(2,i)=index;
vehicle_state(3,i)=port_state(3,index); vehicle_state(4,i)=100;
end
end
%%如果在装货,则时间减一,如果减一后为 0,变为运货状态,此时进货口的状态进行
更新,
%%货物信息进行移位
elseif(vehicle_state(1,i)==1)
vehicle_state(4,i)=vehicle_state(4,i)-1;
if(vehicle_state(4,i)==0)
vehicle_state(1,i)=2;index=vehicle_state(2,i); %%当有一个货物完成装货后,对应 port 货物编号+1,并更新对应 port 信息
port_state(1,index)=port_state(1,index)+1;
port_state(2,index)=task_assignment(port_state(1,index),index);
port_state(3,index)=task_information(port_state(1,index),index);
end
%%处于运货状态时,检测第 i 个车是否到达对应出货口,如果已经到达出货口进行卸货
%%小车状态改为卸货,并将时间置 1000
elseif(vehicle_state(1,i)==2)
delta=vehicle_coordinate(i)-out_coordinate;
index=find((0<delta)&(delta<=0.15));
if(~isempty(index))
if vehicle_state(3,i)==index
vehicle_state(1,i)=3; vehicle_state(4,i)=100;
end
end%%如果在卸货,则时间减一,如果减一后为 0,变为空闲状态,并清空该
车的进货口和出货口信息
elseif(vehicle_state(1,i)==3)
vehicle_state(4,i)=vehicle_state(4,i)-1;
if(vehicle_state(4,i)==0)
vehicle_state(1,i)=0; vehicle_state(2,i)=0; vehicle_state(3,i)=0;
end
end
end
end