顺序结构的基本理解
定义:
把逻辑上相邻的数据元素存储在物理上相邻(占用一片连续的存储单元,中间不能空出来)的存储单元的存储结构

存储位置计算:
L
O
C
(
a
(
i
+
1
)
)
=
L
O
C
(
a
(
i
)
)
+
l
LOC(a(i+1))=LOC(a(i))+l
LOC(a(i+1))=LOC(a(i))+l
L O C ( a ( i ) ) = L O C ( a ( j ) ) + ( i − j ) l LOC(a(i))=LOC(a(j))+(i-j)l LOC(a(i))=LOC(a(j))+(i−j)l
其中 l l l为每个元素所需要占用的存储单元
顺序表的优点:
以物理位置相邻表示逻辑关系,任意元素均可随机存取
顺序表的顺序存储表示:
【地址连续、依次存放、随机存取、类型相同】==>数组(元素)
所以我们可以用一维数组来表示顺序表。但是顺序表长是可以变化的;而数组长度是不可变的,所以我们会额外使用一个变量来表示当前位置在顺序表中的长度
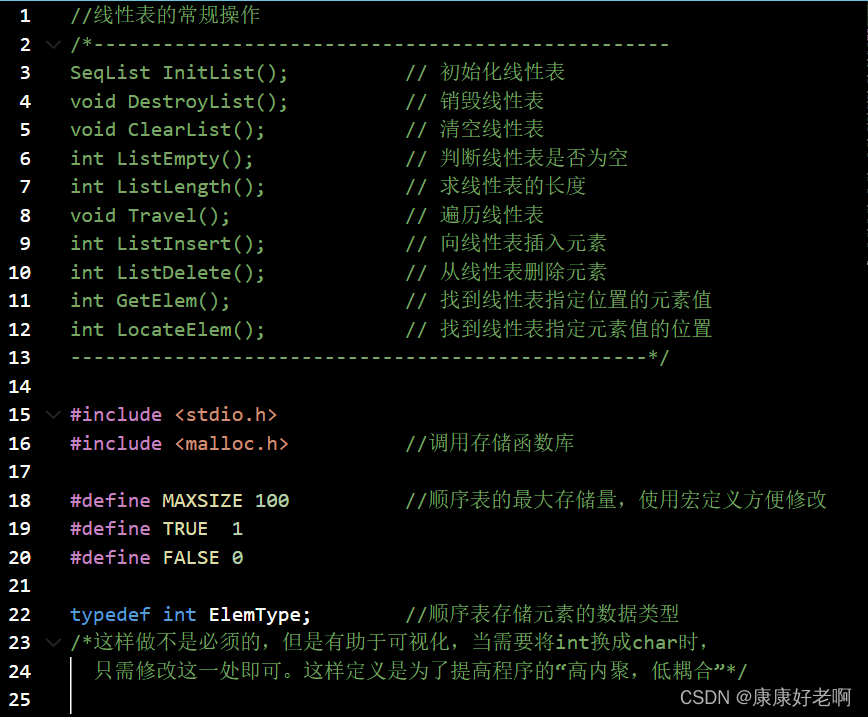
# define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
typedef struct{
ElemType elem[LIST_INIT_SIZE];
int lenth; //当前长度
}SqList
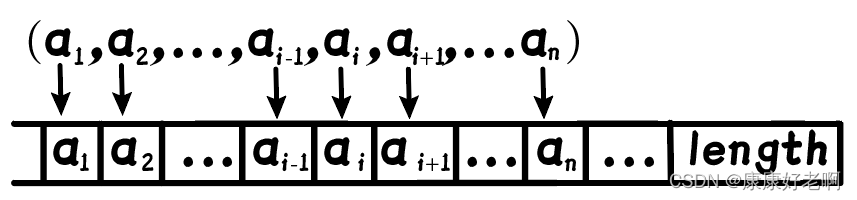
注意:逻辑位序和物理位序相差1(因为数组第一项是a[0])
例子:多项式的顺序存储结构类型定义
P
(
x
)
=
A
x
a
+
B
x
b
+
C
x
c
+
⋅
⋅
⋅
+
Z
(
i
)
x
z
P(x)=Ax^a+Bx^b+Cx^c+···+Z(i)x^z
P(x)=Axa+Bxb+Cxc+⋅⋅⋅+Z(i)xz
其线性表为
P
=
(
(
A
,
a
)
,
(
B
,
b
)
,
(
C
,
c
)
,
.
.
.
,
(
Z
,
z
)
)
P = ( ( A , a ) , ( B , b ) , ( C , c ) , . . . , ( Z , z ) )
P=((A,a),(B,b),(C,c),...,(Z,z))
# define MAXSIZE 1000
typedef struct{ //多项式非零项的意义
float p; //系数
int e; //指数
}Polynomial;
typedef struct{
Polynomial *elem; //存储空间的基地址
int length; //多项式中当前项的系数
}SqList; //多项式的顺序存储结构类型为SqList
补充
补充1:数组静态与动态的区别
| 数组静态分配 | 数组动态分配 |
|---|---|
| typedef struct{ | typedef struct{ |
| ElemType data[maxsize]; | **ElemType *data; ** |
| int length; | int length; |
| }SqList;//顺序表类型 | }SqList;//顺序表类型 |
在数组的静态分配中,data[maxsize]本质上存储的是data[0]的地址;而*data这个指针存储的也是地址,本质上相同。而数组动态分配是由申请储存空间完成的:
SqList L;
L.data = (ElemType*)malloc(sizeof(ElemType)×Maxsize)
补充2:常用函数
需要加载头文件:<stdlib.h>
malloc(m)函数:开辟m字节长度的地址空间,并返回这段空间的首地址
sizeof(x)运算:计算变量x的长度
free§函数:释放指针p所指变量的存储空间,即彻底删除一个变量
(ElemType*)malloc···:强制转换类型方法
补充3:a与b的交换问题
引用类型做参数(C++):
int i=5;
int &j=i;
j是一个引用类型,i的值改变的时候,j的值也会随之发生变化
比如交换a,b的函数,可以有如下两种方式:
| 利用指针类型 | 利用引用类型 |
| ----------------------------- | --------------------------- |
| #include <iostream.h> | #include <iostream.h> |
| void swap(float *m,float *n){ | void swap(float&m,float&n){ |
| float temp; | float temp; |
| temp = *m; | temp=m; |
| *m = *n; | m=n; |
| *n = temp; | n=temp; |
| } | } |
| void main(){ | void main(){ |
| float a,b, *p1, *p2; | float a,b; |
| cin>>a>>b; | cin>>a>>b; |
| p1=&a; p2=&b; | swap(a,b); |
| swap(p1,p2); | count<<a<<endl<<b<<endl; |
| count<<a<<endl<<b<<endl; | } |
| } | |
补充4:宏定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
补充5:内存相关
| 软件 | C | C++ |
|---|---|---|
| 获取内存 | malloc | new |
| 释放内存 | free | delete |
基本操作的实现
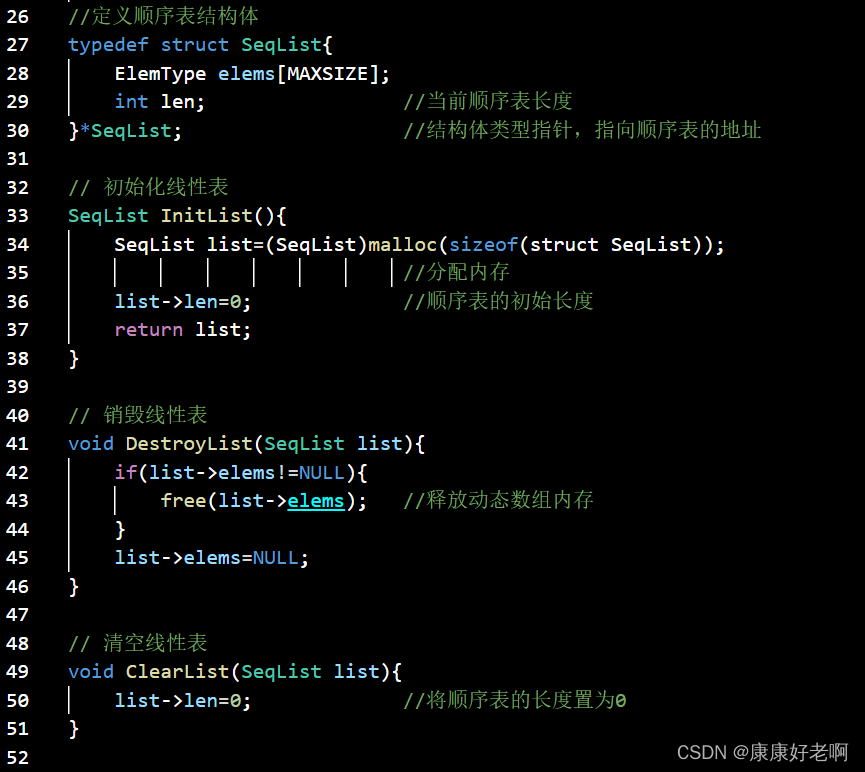
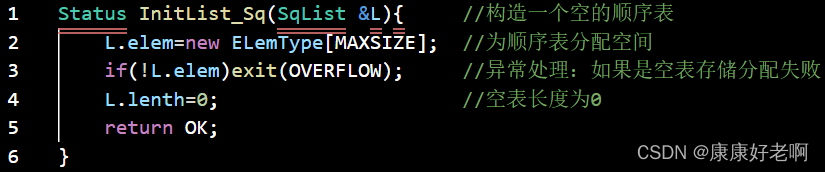
线性表初始化:InitList(&L)
操作结果:构造一个空的线性表L
C++:
C:
线性表销毁:DestoryList(&L)
初始条件:线性表L已经存在
操作结果:销毁线性表L
C++:

C:
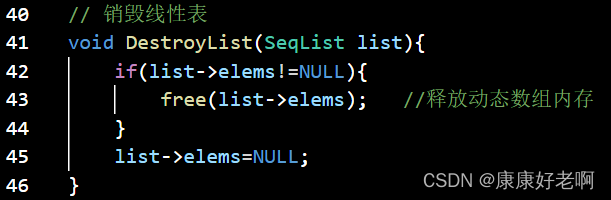
C(1):

线性表清空:ClearList(&L)
初始条件:线性表L已经存在
操作结果:将线性表L重置为空表
C++:

C:

线性表清空判断:ListEmpty(L)
初始条件:线性表L已经存在
操作结果:若线性表L为空表,则返回TRUE;否则返回FALSE
C++:
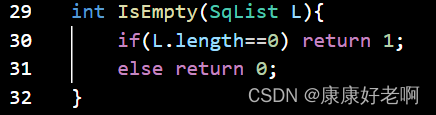
C:
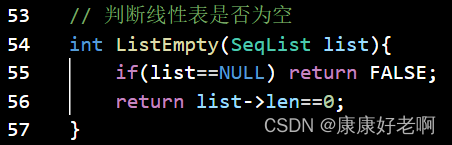
线性表长度:ListLength(L)
初始条件:线性表L已经存在
操作结果:返回线性表L中的数据元素个数
C++:
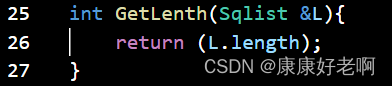
C:
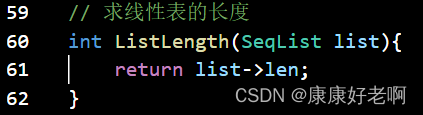
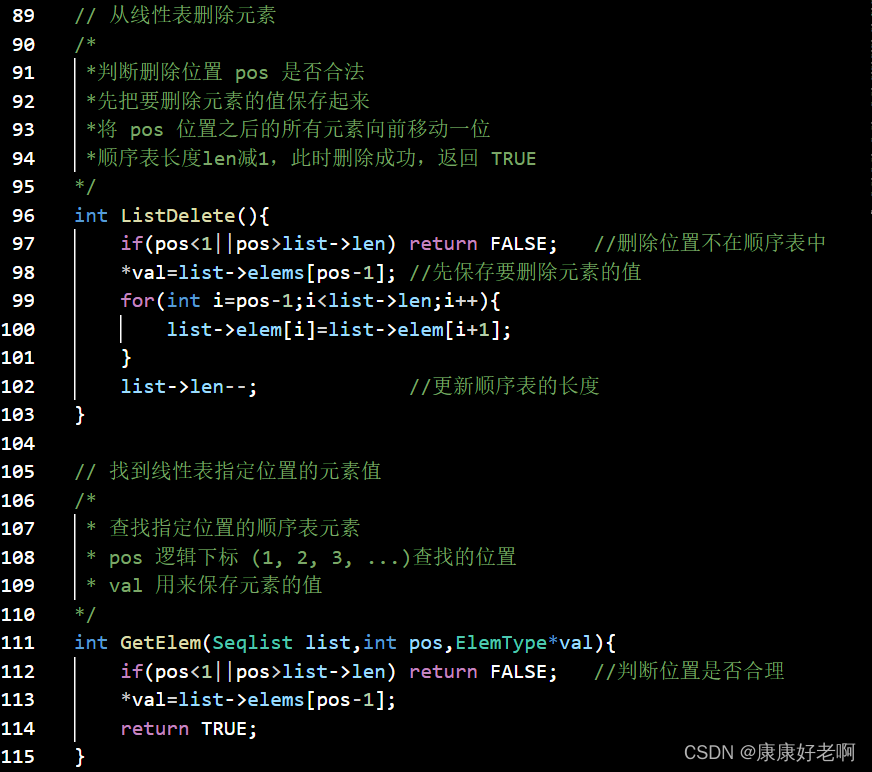
线性表查找:GetElem(L,i,&e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)
操作结果:用e返回线性表L中第i个数据元素的值
C++:

C:

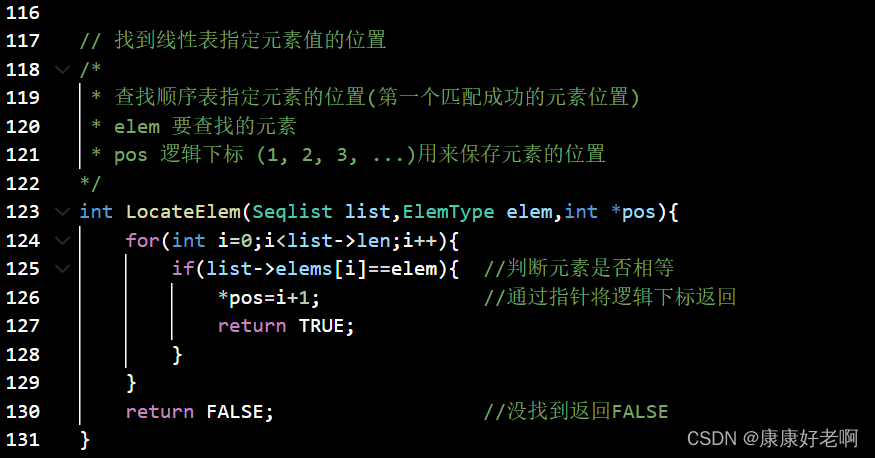
线性表定位:LocateElem(L,e,compare())
**初始条件:**线性表L已经存在,compare()是数据元素的判定函数
**操作结果:**返回L中第1个与e满足compare()的数据元素的位序。这样的元素不存在则返回值为0
C++:
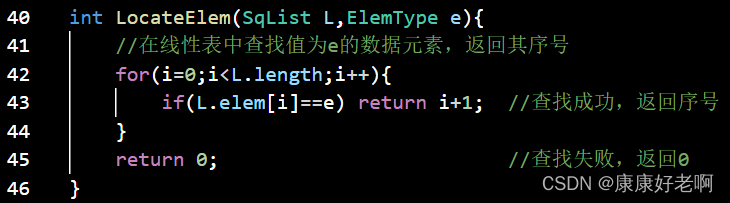
C:
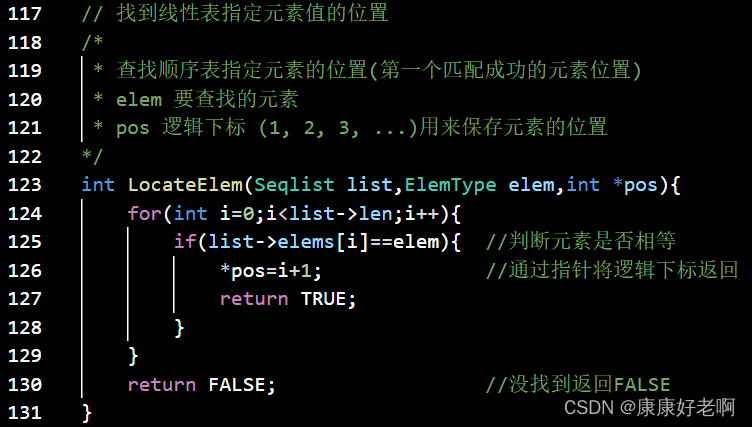
算法分析:
频度(平均查找长度为)期望值为
(
1
+
2
+
3
+
4
+
5
+
6
+
⋅
⋅
⋅
+
n
−
1
+
n
)
/
n
=
(
n
+
1
)
/
2
(1+2+3+4+5+6+···+n-1+n)/n=(n+1)/2
(1+2+3+4+5+6+⋅⋅⋅+n−1+n)/n=(n+1)/2
拓展一下:
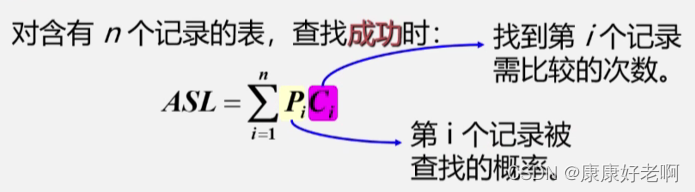
上图的情况就是当查找概率都相等时的结果。
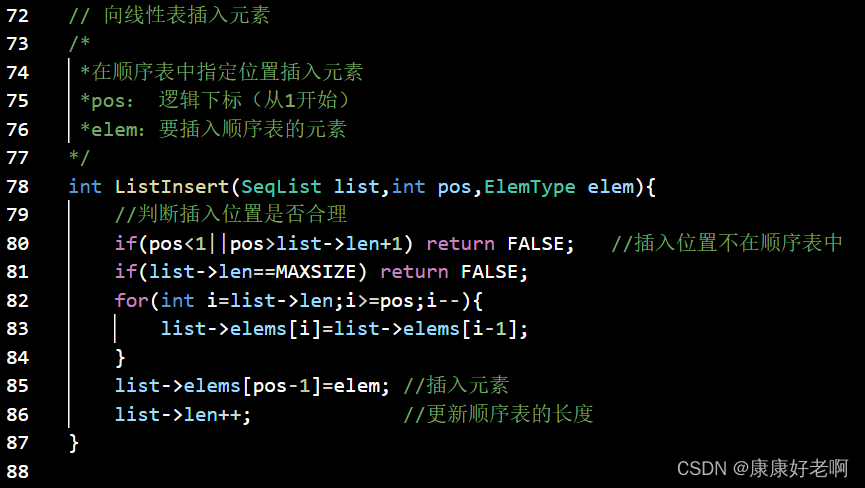
线性表元素插入:ListInsert(&L,i,e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)+1
操作结果:在L的第i个位置插入新的数据元素e,L的长度加一
算法思想:
1)判断插入位置i是否合法。
2)判断顺序表的存储空间是否已满,若已经满了返回ERROR
C:
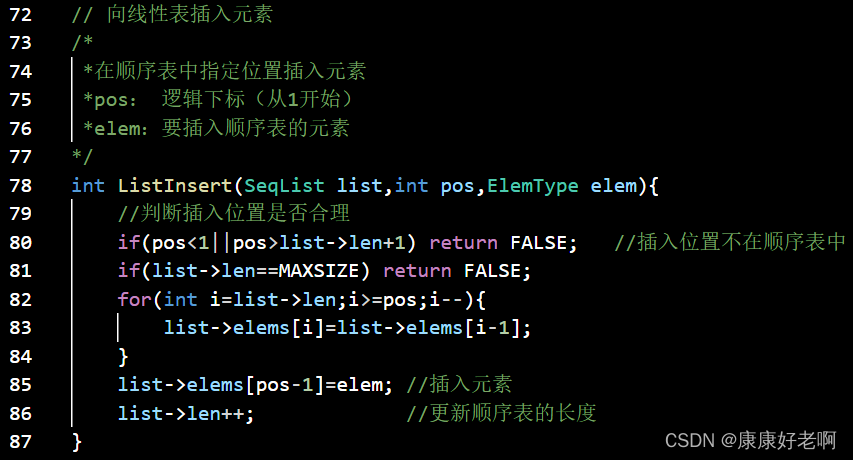
算法分析:
插入的位置有如下三种情况:
① 插在位置最后,则根本不需要移动,速度较快
② 插在位置中间,则需要移动一定数量的元素,速度适中
③ 插在位置最前,则需要将表中所有元素后移,速度很慢
那么平均的情况如何?
我们知道总共有n+1个插入位置,第i个插入位置需要移动n-i+1次,则
(
1
+
2
+
3
+
4
+
5
+
6
+
⋅
⋅
⋅
+
n
−
1
+
n
)
/
(
n
+
1
)
=
n
/
2
(1+2+3+4+5+6+···+n-1+n)/(n+1)=n/2
(1+2+3+4+5+6+⋅⋅⋅+n−1+n)/(n+1)=n/2
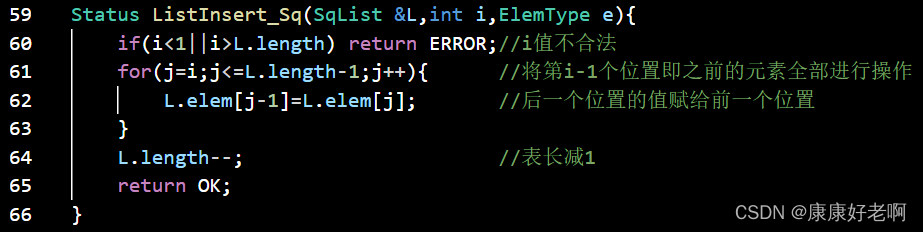
线性表元素删除:ListDelete(&L,i,&e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)
操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减一
算法思想:
① 判断删除位置i是否合法(合法值1≤i≤n)
② 将欲删除的元素保留在e中
③ 将第i+1至第n位的元素依次向前移动一个位置
④ 表长减1,删除成功返回OK
C++:
C:
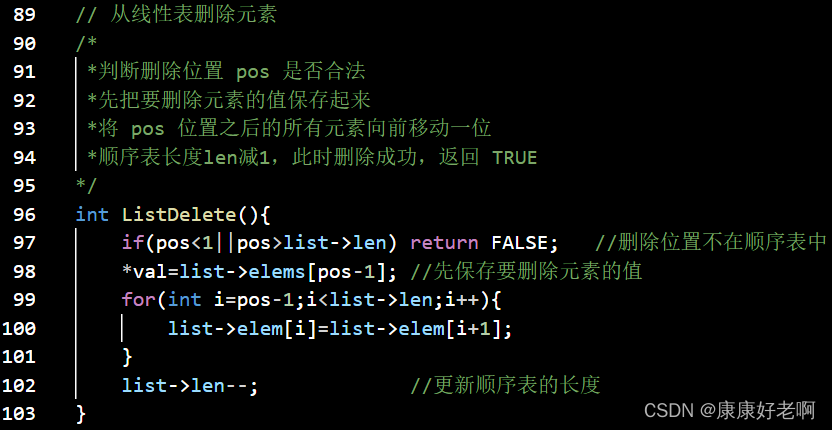
算法分析:此处的分析与线性表元素的插入十分类似,
(
1
+
2
+
3
+
4
+
5
+
6
+
⋅
⋅
⋅
+
n
−
1
)
/
n
=
(
n
−
1
)
/
2
(1+2+3+4+5+6+···+n-1)/n=(n-1)/2
(1+2+3+4+5+6+⋅⋅⋅+n−1)/n=(n−1)/2
顺序表总结:
优点:
· 存储密度大(结点本身所占储存量/结点结构所占存储量)
· 可以随机存取表中任意元素
缺点:
· 插入删除某元素时需要移动大量元素
· 浪费存储空间
· 属于静态存储形式,数据元素不能自由扩充
附录:顺序表完整C源码