摘要

剑指 Offer 66. 构建乘积数组

一、左右乘积列表

我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案，而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。对于给定索引i，我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。

算法详解：

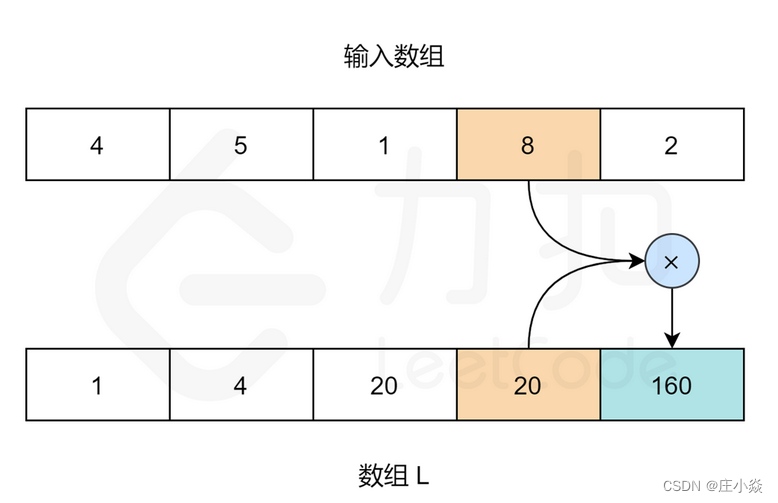
初始化两个空数组 L 和 R。对于给定索引 i，L[i] 代表的是 i 左侧所有数字的乘积，R[i] 代表的是 i 右侧所有数字的乘积。
我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L，L[0] 应该是 1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * a[i-1]。
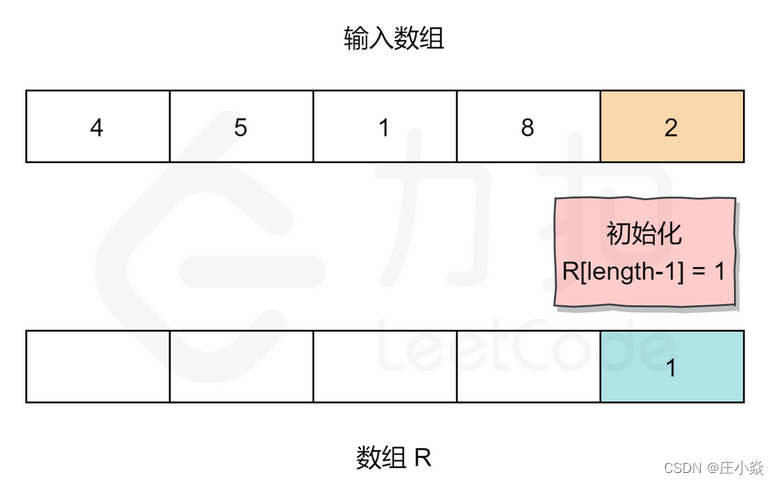
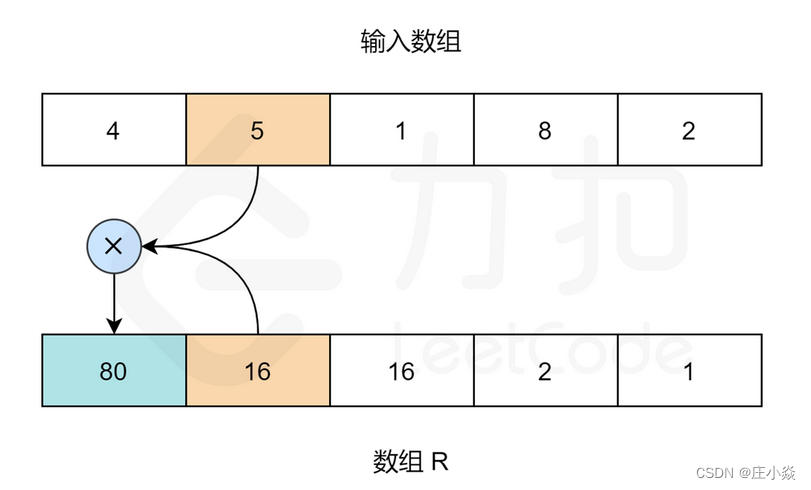
同理，对于数组 R，R[length-1] 应为 1。length 指的是输入数组的大小。其他元素：R[i] = R[i+1] * a[i+1]。
当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i]。

package Array;

/**
 * @Classname JZ66构建乘积数组
 * @Description TODO
 * @Date 2023/3/8 21:14
 * @Created by xjl
 */
public class JZ66构建乘积数组 {

    public int[] constructArr(int[] a) {
        int length = a.length;

        // L 和 R 分别表示左右两侧的乘积列表
        int[] L = new int[length];
        int[] R = new int[length];

        int[] answer = new int[length];

        // L[i] 为索引 i 左侧所有元素的乘积
        // 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
        L[0] = 1;
        for (int i = 1; i < length; i++) {
            L[i] = a[i - 1] * L[i - 1];
        }

        // R[i] 为索引 i 右侧所有元素的乘积
        // 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
        R[length - 1] = 1;
        for (int i = length - 2; i >= 0; i--) {
            R[i] = a[i + 1] * R[i + 1];
        }

        // 对于索引 i，除 a[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for (int i = 0; i < length; i++) {
            answer[i] = L[i] * R[i];
        }
        return answer;
    }
}

复杂度分析

时间复杂度：O(N)，其N指的是数组a的大小。预处理L和R数组以及最后的遍历计算都是 O(N)的时间复杂度。
空间复杂度：O(N)，其中N指的是数组a的大小。使用了L和R数组去构造答案，L和R数组的长度为数组 a 的大小。

二、优化方法

尽管上面的方法已经能够很好的解决这个问题，但是空间复杂度并不为常数。由于输出数组不算在空间复杂度内，那么我们可以将 L 或 R 数组用输出数组来计算。先把输出数组当作 L 数组来计算，然后再动态构造 R 数组得到结果。让我们来看看基于这个思想的算法。

算法详解

初始化 answer 数组，对于给定索引 i，answer[i] 代表的是 i 左侧所有数字的乘积。
构造方式与之前相同，只是我们试图节省空间，先把answer作为方法一的 L 数组。
这种方法的唯一变化就是我们没有构造R数组。而是用一个遍历来跟踪右边元素的乘积。并更新数组 answer[i]=answer[i]∗R。然后 RR 更新为 R=R∗a[i]，其中变量R表示的就是索引右侧数字的乘积

public int[] productExceptSelf(int[] a) {
        int length = a.length;
        int[] answer = new int[length];

        // answer[i] 表示索引 i 左侧所有元素的乘积
        // 因为索引为 '0' 的元素左侧没有元素， 所以 answer[0] = 1
        answer[0] = 1;
        for (int i = 1; i < length; i++) {
            answer[i] = a[i - 1] * answer[i - 1];
        }

        // R 为右侧所有元素的乘积
        // 刚开始右边没有元素，所以 R = 1
        int R = 1;
        for (int i = length - 1; i >= 0; i--) {
            // 对于索引 i，左边的乘积为 answer[i]，右边的乘积为 R
            answer[i] = answer[i] * R;
            // R 需要包含右边所有的乘积，所以计算下一个结果时需要将当前值乘到 R 上
            R *= a[i];
        }
        return answer;
    }

复杂度分析