Codeforces Round 855 (Div. 3) A-E2

news2024/10/1 17:31:00

比赛链接：Dashboard - Codeforces Round 855 (Div. 3) - Codeforces

A：模拟 

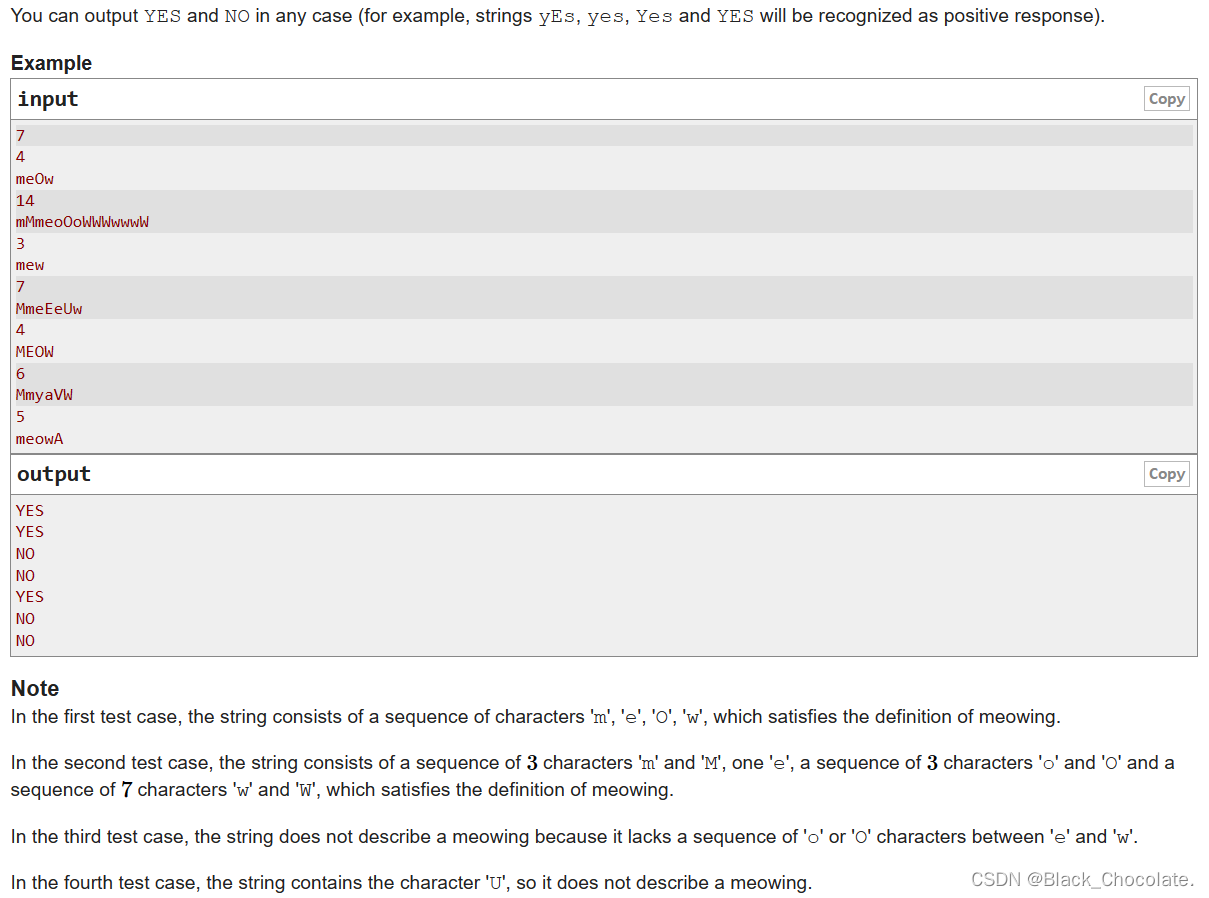题意：给定一个字符串，问这个字符串是不是猫叫。定义是猫叫得字符串：

1：必须由大写或小写得'M（m）','E（e）','O（o）','W（w）'组成

2：字符串起始必须是M（大写或者小写都行）紧跟其后必须是E，接着是O，接着是W，然后结束。

分析：根据条件，将字符串扫一遍即可

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p

inline void solve(){
	int n,i=0;string s;
	cin>>n>>s;
	if(n<4||(s[0]!='M'&&s[0]!='m')){
		cout<<"NO\n";return;
	}
	while(s[i]=='M'||s[i]=='m') i++;
	if(s[i]!='E'&&s[i]!='e'){
		cout<<"NO\n";return;
	}
	while(s[i]=='E'||s[i]=='e') i++;
	if(s[i]!='O'&&s[i]!='o'){
		cout<<"NO\n";return;
	}
	while(s[i]=='O'||s[i]=='o') i++;
	if(s[i]!='W'&&s[i]!='w'){
		cout<<"NO\n";return;
	}
	while(s[i]=='W'||s[i]=='w') i++;
	if(i==n) cout<<"YES\n";
	else cout<<"NO\n"; 
}

signed main(){
	fast;int T;cin>>T;
	while(T--) solve();
}

 B：贪心

题意： 给定一个字符串，相同字符的大小写为一个匹配对（例如：Aa）。你可以使用任意次操作，使得将大写字母改为小写字母，或者小写字母改为大写字母。问最多有多少个匹配对

分析：我们发现，尽可能的使用完操作次数，我们才会得到最大匹配对数。我们只需要记录一下相同字母对应的大小写个数，然后可以先计算原始的匹配对，再计算操作后的匹配对数。具体看代码

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int u[N],l[N];

inline void solve(){
	int n,k;string s;cin>>n>>k>>s;
	memset(u,0,sizeof u);memset(l,0,sizeof l);
	for(int i=0;i<n;i++){
		if(isupper(s[i])) u[s[i]-'A']++;
		else l[s[i]-'a']++;
	}
	int ans=0;
	for(int i=0;i<26;i++){
		int minn=min(u[i],l[i]);
		ans+=minn;
		u[i]-=minn;l[i]-=minn;
		if(u[i]>=2){
			if(u[i]/2<=k) ans+=u[i]/2,k-=u[i]/2;
			else ans+=k,k=0;
		}
		else if(l[i]>=2){
			if(l[i]/2<=k) ans+=l[i]/2,k-=l[i]/2;
			else ans+=k,k=0;
		}
	}
	cout<<ans<<"\n";
}

signed main(){
	fast;int T;cin>>T;
	while(T--) solve();
}

 C:模拟+贪心（大根堆）

 

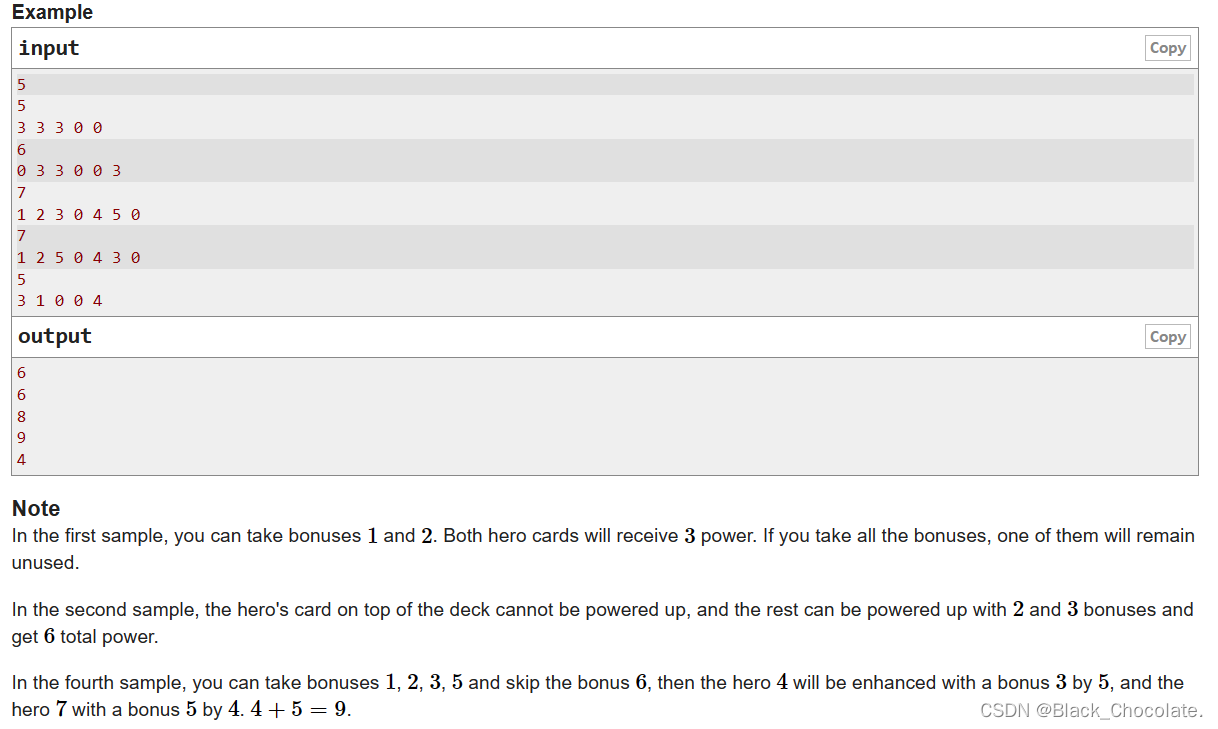题意：你的初始分数为0。给定一堆牌，每个牌有一定的数字，给定顺序去摸取。如果摸到非0牌，则可以选择将此牌放在自己牌堆的堆顶，或者放弃这张牌。如果摸到数字为0的牌，则自己牌堆堆顶的数字会加到你的分数里面，并且标记这张牌已经使用过，问你能得到的最大分数。

分析：根据题意，我们发现，在摸到非0牌之前，我们要将最大的数字放在堆顶，那么这是一个动态维护最大值的过程，因此我们可以使用大根堆。大根堆的pop（）操作即为已经使用的牌。

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int a[N];

inline void solve(){
	int n;cin>>n;
	priority_queue<int>q;
	for(int i=1;i<=n;i++) cin>>a[i];
	int ans=0,cnt=1;
	while(1){
		if(cnt>n) break;
		while(cnt<=n&&a[cnt]!=0) q.push(a[cnt++]);
		while(cnt<=n&&a[cnt]==0){
			if(!q.size()){
				cnt++;continue;
			}
			else{
				ans+=q.top();
				q.pop();
				cnt++;
			}
		}
	}
	cout<<ans<<"\n";
}

signed main(){
	fast;int T;cin>>T;
	while(T--) solve();
}

D:思维

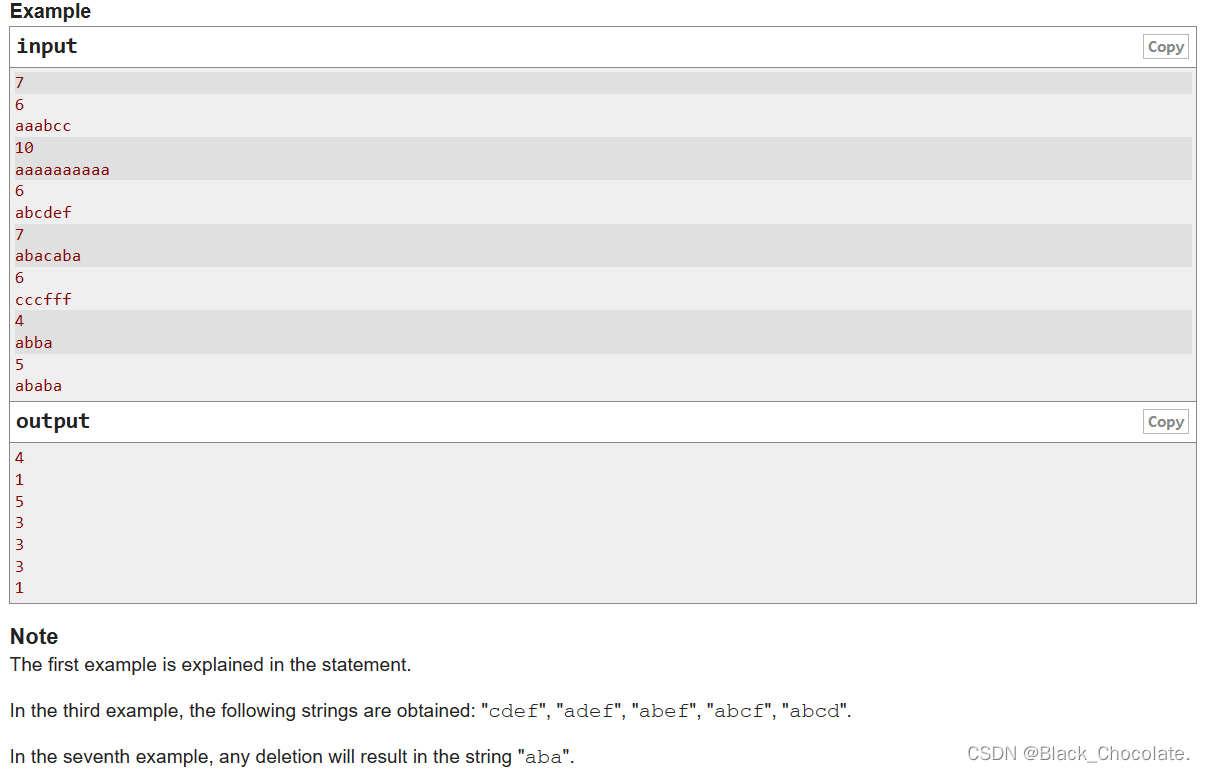
题意：给定字符串 s，你可以移除其中两个连续的字母。问操作之后你所能得到的不同字符串的数量是多少

分析：我们发现，如果这样一组字符串：aba，那么删掉两个相邻的元素，所得的结果串是一样的。那么我们可以得出一个结论：如果s[i]==s[i+2],那么就说明有一个重复串的出现。

此外还有一个结论可以从样例得出：如果一个长度为n的串所含的不同字符个数为n，那么可以得到n-1个不同的串。因此，我们只需要减掉重复串的个数即可。

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p
int a[N];

inline void solve(){
	int n;string s;cin>>n>>s;
	int ans=0;
	for(int i=0;i<n-2;i++){
		if(s[i]==s[i+2]) ans++;
	}
	cout<<n-ans-1<<"\n";
}

signed main(){
	fast;int T;cin>>T;
	while(T--) solve();
}

 E:思维

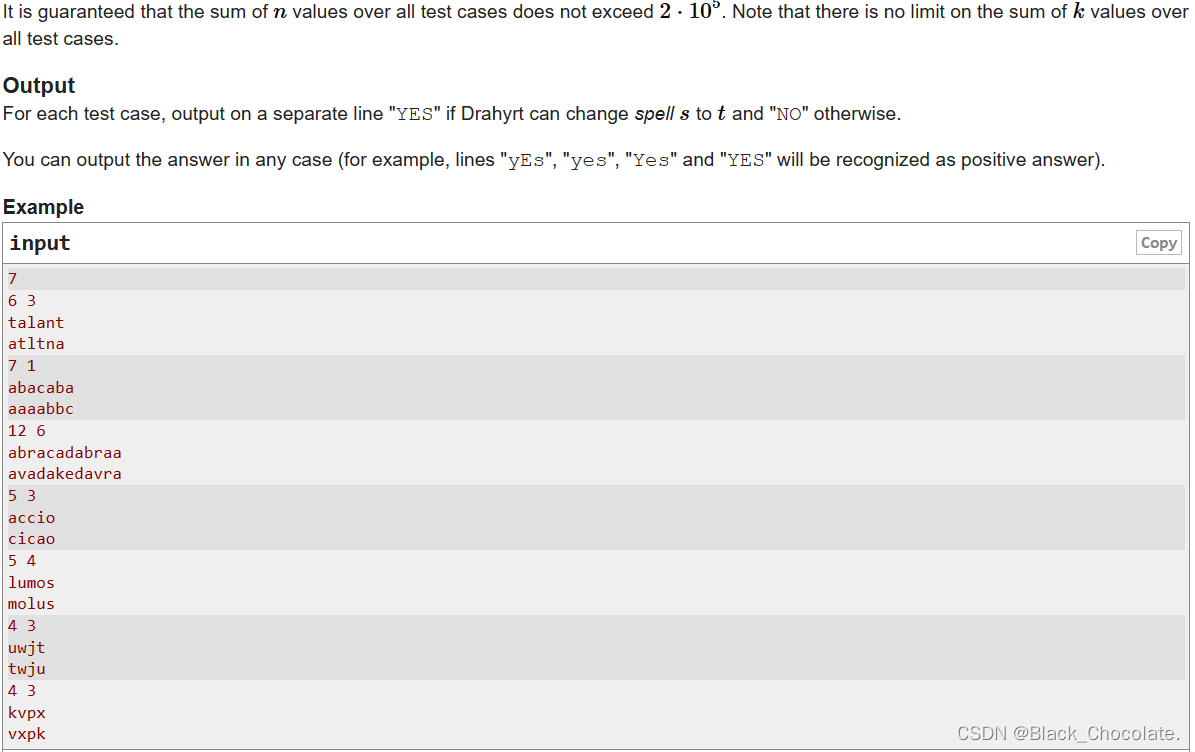
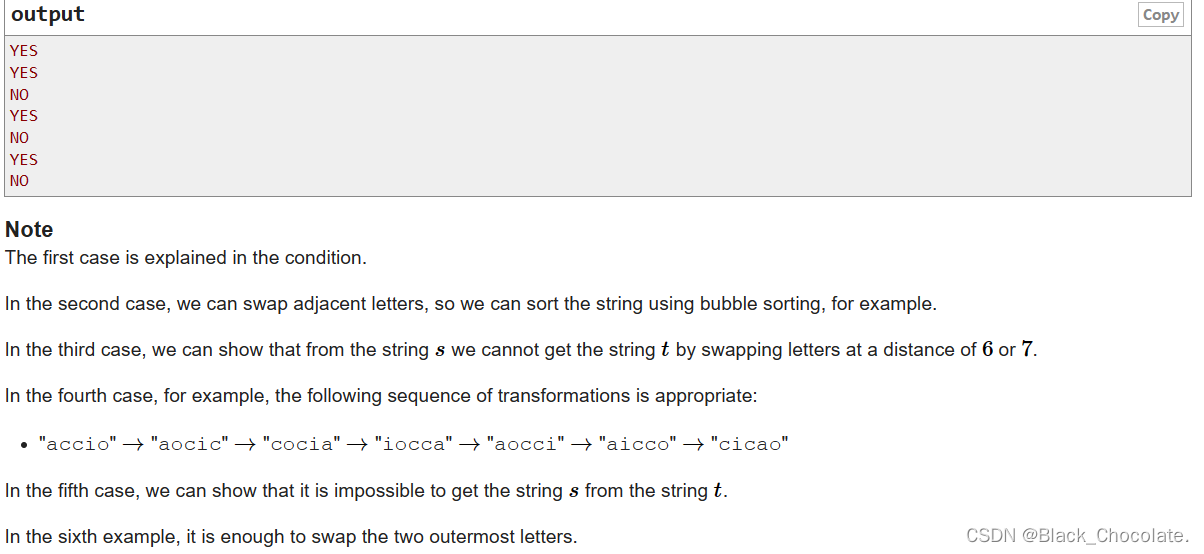
题意：给定两个字符串和k，字符串可以将下标 和|i−j|=k和|i−j|=k+1 得两个字符 ，ai，aj 发生交换

分析：通过手撸样例可以发现：如果当n=5，k=3的时候，满足条件的点为：[1,4],[1,5],[2,5]。然后你会发现：点1，2，4，5的位置可以任意交换。位置3则不能交换。所以思路很显然了。

首先判断两个字符串中包含的字符数是否相同，再判断不能交换位置的点上的字符是否相同。

代码：

#include <bits/stdc++.h>
#define pi acos(-1)
#define int long long
#define PII pair<int,int>
#define all(v) v.begin(),v.end()
#define INF 0x3f3f3f3f3f3f3f3f
#define fs(a) cout<<fixed<<setprecision(a)<< //fs(4)(1.0/3)=0.3333//保留a位小数
#define read() freopen("input.txt","r",stdin)
#define output() freopen("output.txt","w",stdout)
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
using namespace std;
const int N=2e5+10;
const int mod = 1e9+7;
const int Mod = 998244353;
int lowbit(int x){return x&(-x);}
int up(int a,int b){return a<0?a/b:(a+b-1)/b;}//       a/b向上取整
int quickpow(int a,int n){int ans=1;while(n){if(n&1){ans*=a,ans%=Mod;}a*=a;a%=Mod;n>>=1;}return ans;}//快速幂
int qc(int a,int b,int p){int ans=0;while(b){if(b&1){ans+=a,ans%=p;}a*=2;a%=p;b>>=1;}return ans;}//快速乘 a*b%p

inline bool pd(string a,string b){
	map<char,int>mp1,mp2;
	for(int i=0;i<a.size();i++) mp1[a[i]]++;
	for(int i=0;i<b.size();i++) mp2[b[i]]++;
	for(auto x:a){
		if(mp1[x]!=mp2[x]) return false;
	}
	return true;
}

inline void solve(){
	int n,k;string s,t;
	cin>>n>>k>>s>>t;
	if(!pd(s,t)){
		cout<<"NO\n";return;
	}
	bool ok=true;
	for(int i=0;i<n;i++){
		if(i<k&&n-i-1<k&&s[i]!=t[i]){
			ok=false;break;
		}
	}
	if(ok) cout<<"YES\n";
	else cout<<"NO\n";
}

signed main(){
	fast;int T;cin>>T;
	while(T--) solve();
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/398012.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【大数据是什么】

【大数据是什么】

大数据是什么大数据是做什么的&#xff1f;大数据主要有哪些职位 &#xff1f;大数据运维工程师数据仓库开发工程师ETL工程师大数据开发工程师BI工程师算法工程师大数据平台开发工程师大数据架构师讲述一下自己的大数据学习之路大数据是做什么的&#xff1f; 2014年&#xff0c…
阅读更多...
Pytorch语义分割网络的详细训练过程——以NYUv2数据集为例

Pytorch语义分割网络的详细训练过程——以NYUv2数据集为例

目录一、构建数据集1. 对Dataset和DataLoader的理解2. torch.utils.data.Dataset3. torch.utils.data.DataLoader4. 代码分块解析5. 完整代码6. 可视化二、模型搭建三、定义损失函数和优化器四、迭代训练参考文章一、构建数据集 1. 对Dataset和DataLoader的理解 Pytorch提供了…
阅读更多...
[ROC-RK3568-PC] [Firefly-Android] 10min带你了解RTC的使用

[ROC-RK3568-PC] [Firefly-Android] 10min带你了解RTC的使用

&#x1f347; 博主主页&#xff1a; 【Systemcall小酒屋】&#x1f347; 博主追寻&#xff1a;热衷于用简单的案例讲述复杂的技术&#xff0c;“假传万卷书&#xff0c;真传一案例”&#xff0c;这是林群院士说过的一句话&#xff0c;另外“成就是最好的老师”&#xff0c;技术…
阅读更多...
c++11 标准模板（STL）（std::unordered_map）（六）

c++11 标准模板（STL）（std::unordered_map）（六）

定义于头文件 <unordered_map> template< class Key, class T, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator< std::pair<const Key, T> > > class unordered…
阅读更多...
【Transformers】IMDB 分类

【Transformers】IMDB 分类

安装 transformers 库。 !pip install transformersimport numpy as np import pandas as pd import tensorflow as tf import tensorflow_datasets as tfdsfrom transformers import BertTokenizer from sklearn.model_selection import train_test_split from transformers i…
阅读更多...
IO学习、拓展贴

IO学习、拓展贴

1. 字节流 1.1 FileInputStream import org.junit.jupiter.api.Test;import java.io.FileInputStream; import java.io.FileNotFoundException; import java.io.IOException;/*** 演示FileInputStream的使用(字节输入流 文件--> 程序)*/ public class FileInputStream_ {pu…
阅读更多...
10款最佳项目管理工具推荐，总有一款适合你

10款最佳项目管理工具推荐，总有一款适合你

为什么需要项目管理工具&#xff1f; 如今企业规模不断扩大&#xff0c;业务逐渐复杂化&#xff0c;项目管理已经成为现代企业管理中不可或缺的一环&#xff1b; 如果没有合适的项目管理工具&#xff0c;我们的项目管理和跟踪就会变得非常困难。这可能导致项目延期或者出现一…
阅读更多...
免费Api接口汇总（亲测可用，可写项目）

免费Api接口汇总（亲测可用，可写项目）

免费Api接口汇总&#xff08;亲测可用&#xff09;1. 聚合数据2. 用友API3. 天行数据4. Free Api5. 购物商城6. 网易云音乐API7. 疫情API8. 免费Api合集1. 聚合数据 https://www.juhe.cn/ 2. 用友API http://iwenwiki.com/wapicovid19/ 3. 天行数据 https://www.tianapi.com…
阅读更多...
RK356x U-Boot研究所（命令篇）3.9 scsi命令的用法

RK356x U-Boot研究所（命令篇）3.9 scsi命令的用法

平台U-Boot 版本Linux SDK 版本RK356x2017.09v1.2.3文章目录 一、设备树与config配置二、scsi命令的定义三、scsi命令的用法3.1 scsi总线扫描3.2 scsi设备读写一、设备树与config配置 RK3568支持SATA接口，例如ROC-RK3568-PC： 原理图如下： 可以新建一个rk3568-sata.config配…
阅读更多...
Oracle listagg，wm_concat函数行转列结果去重Oracle 11g/19c版本

Oracle listagg，wm_concat函数行转列结果去重Oracle 11g/19c版本

1、准备数据表 2、根据学生名(stu_name)分组&#xff0c;学生名相同的&#xff0c;学生年龄(stu_age)用逗号拼接&#xff0c;使用 listagg&#xff08;&#xff09;函数法拼接 3、上图中出现了两个12,12&#xff0c;实现去重 3.1 listagg&#xff08;&#xff09; 函数 去重 【…
阅读更多...
网络协议(十一)：单向散列函数、对称加密、非对称加密、混合密码系统、数字签名、证书

网络协议(十一)：单向散列函数、对称加密、非对称加密、混合密码系统、数字签名、证书

网络协议系列文章 网络协议(一)&#xff1a;基本概念、计算机之间的连接方式 网络协议(二)&#xff1a;MAC地址、IP地址、子网掩码、子网和超网 网络协议(三)&#xff1a;路由器原理及数据包传输过程 网络协议(四)&#xff1a;网络分类、ISP、上网方式、公网私网、NAT 网络…
阅读更多...
怎么把tif格式转成jpg？快速无损转换

怎么把tif格式转成jpg？快速无损转换

怎么把tif格式转成jpg&#xff1f;在编辑使用图片的时候&#xff0c;弄清各种图片格式的特点是很重要的&#xff0c;因为图片总因自身格式具备的特点不同常常出现打不开的情况&#xff0c;或者占的体积大&#xff0c;这都会直接影响我们的使用。所以目前很多的图片格式都需要提…
阅读更多...
spring boot整合RabbitMQ

spring boot整合RabbitMQ

文章目录 目录 文章目录 前言 一、环境准备 二、使用步骤 2.1 RabbitMQ高级特性 2.1.1 消息的可靠性传递 2.1.2 Consumer Ack 2.2.3 TTL 2.2.4 死信队列 总结 前言 一、环境准备 引入依赖生产者和消费都引入这个依赖 <dependency><groupId>org.springframework…
阅读更多...
自动化测试总结--断言

自动化测试总结--断言

采购对账测试业务流程中&#xff0c;其中一个测试步骤总是失败&#xff0c;原因是用例中参数写错及断言不明确 一、问题现象&#xff1a; 采购对账主流程中&#xff0c;其中一个步骤失败了&#xff0c;会导致这个套件一直失败 图&#xff08;1&#xff09;测试报告视图中&…
阅读更多...
Navicate远程连接Linux上docker安装的MySQL容器

Navicate远程连接Linux上docker安装的MySQL容器

Navicate远程连接Linux上docker安装的MySQL容器失败 来自&#xff1a;https://bluebeastmight.github.io/ 问题描述&#xff1a;windows端的navicat远程连接不上Linux上docker安装的mysql&#xff08;5.7版本&#xff09;容器&#xff0c;错误代码10060 标注&#xff1a; 1、…
阅读更多...
XSS攻击防御

XSS攻击防御

XSS攻击防御XSS Filter过滤方法输入验证数据净化输出编码过滤方法Web安全编码规范XSS Filter XSS Filter的作用是通过正则的方式对用户&#xff08;客户端&#xff09;请求的参数做脚本的过滤&#xff0c;从而达到防范XSS攻击的效果。 XSS Filter作为防御跨站攻击的主要手段之…
阅读更多...
C++ Primer阅读笔记--书包程序

C++ Primer阅读笔记--书包程序

1--该章节新知识点 ① 在 UNIX 和 Windows 系统中&#xff0c;执行完一个程序后&#xff0c;可以通过 echo 命令获得其返回值&#xff1b; # UNIX系统中&#xff0c;通过如下命令获得状态 echo $? ② 在标准库中&#xff0c;定义了两个输出流 ostream 对象&#xff1a;cerr…
阅读更多...
运维效率狂飙，都在告警管理上

运维效率狂飙，都在告警管理上

随着数字化进程的加速&#xff0c;企业IT设备和系统越来越多&#xff0c;告警和流程中断风险也随之增加。每套系统和工具发出的警报&#xff0c;听起来像是一场喧嚣的聚会&#xff0c;各自谈论不同的话题。更糟糕的是&#xff0c;安全和运维团队正在逐渐丧失对告警的敏感度&…
阅读更多...
2.Fully Convolutional Networks for Semantic Segmentation论文记录

2.Fully Convolutional Networks for Semantic Segmentation论文记录

欢迎访问个人网络日志&#x1f339;&#x1f339;知行空间&#x1f339;&#x1f339; 文章目录1.基础介绍2.分类网络转换成全卷积分割网络3.转置卷积进行上采样4.特征融合5.一个pytorch源码实现参考资料1.基础介绍 论文:Fully Convolutional Networks for Semantic Segmentati…
阅读更多...
如何用postman实现接口自动化测试

如何用postman实现接口自动化测试

postman使用 开发中经常用postman来测试接口&#xff0c;一个简单的注册接口用postman测试&#xff1a; 接口正常工作只是最基本的要求&#xff0c;经常要评估接口性能&#xff0c;进行压力测试。 postman进行简单压力测试 下面是压测数据源&#xff0c;支持json和csv两个格…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023