🎆音乐分享

（点击链接可以听哦😎） 

无名之辈 - 陈雪燃
 

---

目录

归并排序 

 归并排序应用

---

文章中的图片来源：

(2条消息) 归并排序（分治法）_分治法 归并排序_小小的香辛料的博客-CSDN博客

AcWing 787. 归并排序 - AcWing 

AcWing 788. 逆序对的数量--图解 - AcWing 

🍔🍔🍔🍔🍔🍔

之前寒假学过，但是又忘了，所以写一下博客，记录一下，方便复习

🍔🍔🍔🍔🍔🍔 

归并排序 

787. 归并排序 - AcWing题库 

 

 

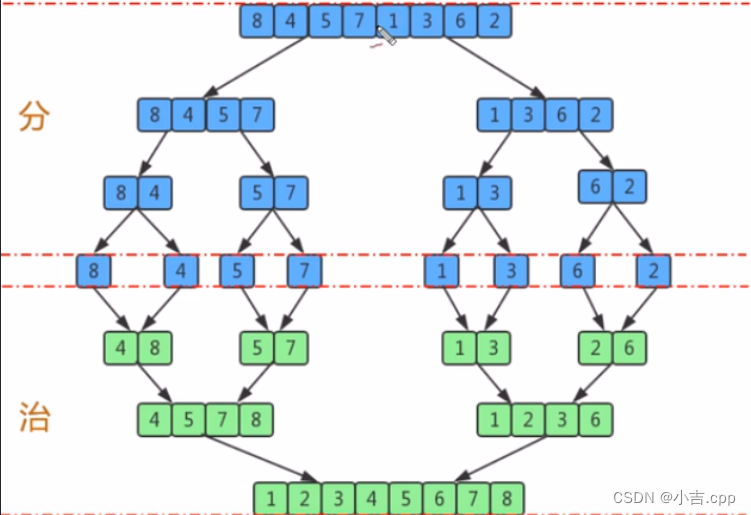
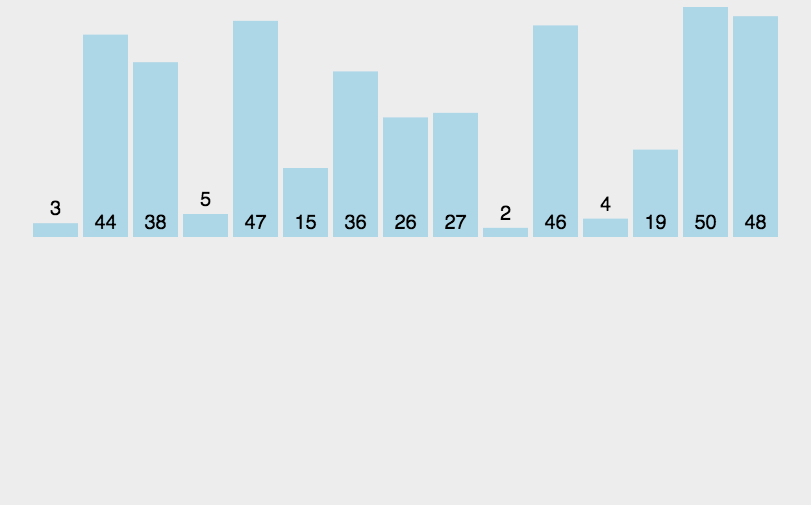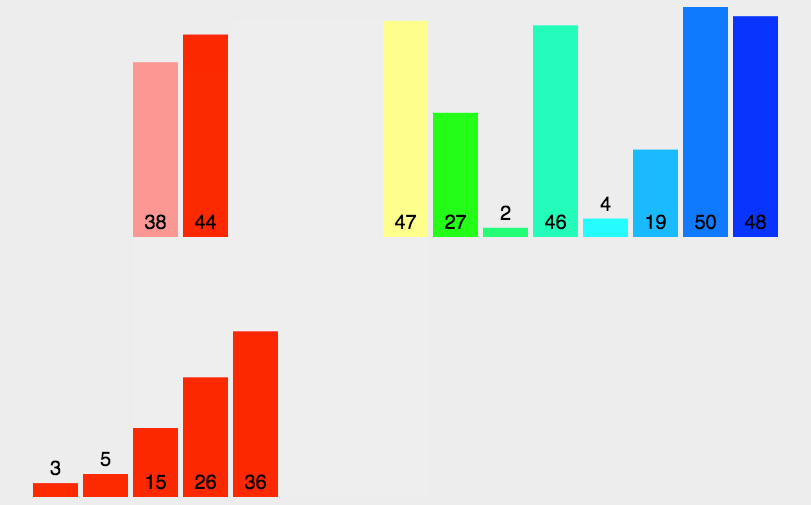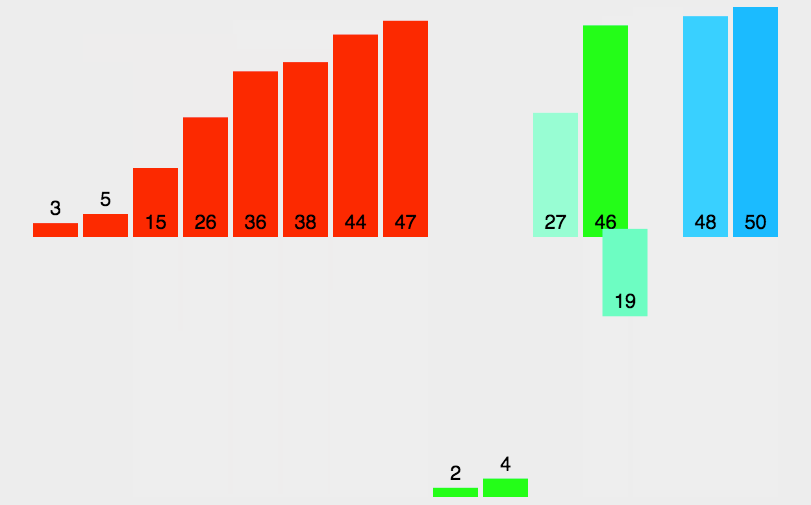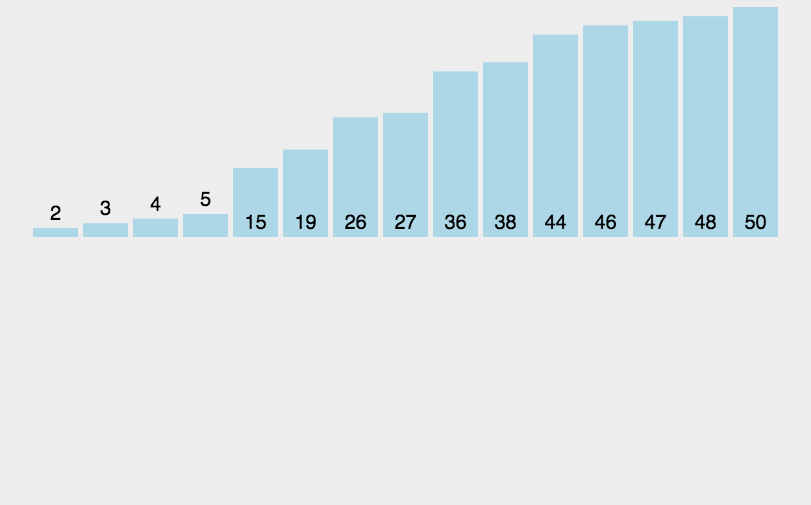
代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
int q[N], w[N];

void merge_sort(int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;

    merge_sort(l, mid), merge_sort(mid + 1, r);

    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r)
        if (q[i] < q[j]) w[k ++ ] = q[i ++ ];
        else w[k ++ ] = q[j ++ ];
    while (i <= mid) w[k ++ ] = q[i ++ ];
    while (j <= r) w[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = w[j];
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    merge_sort(0, n - 1);

    for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);

    return 0;
}

 归并排序应用

 788. 逆序对的数量 - AcWing题库

 

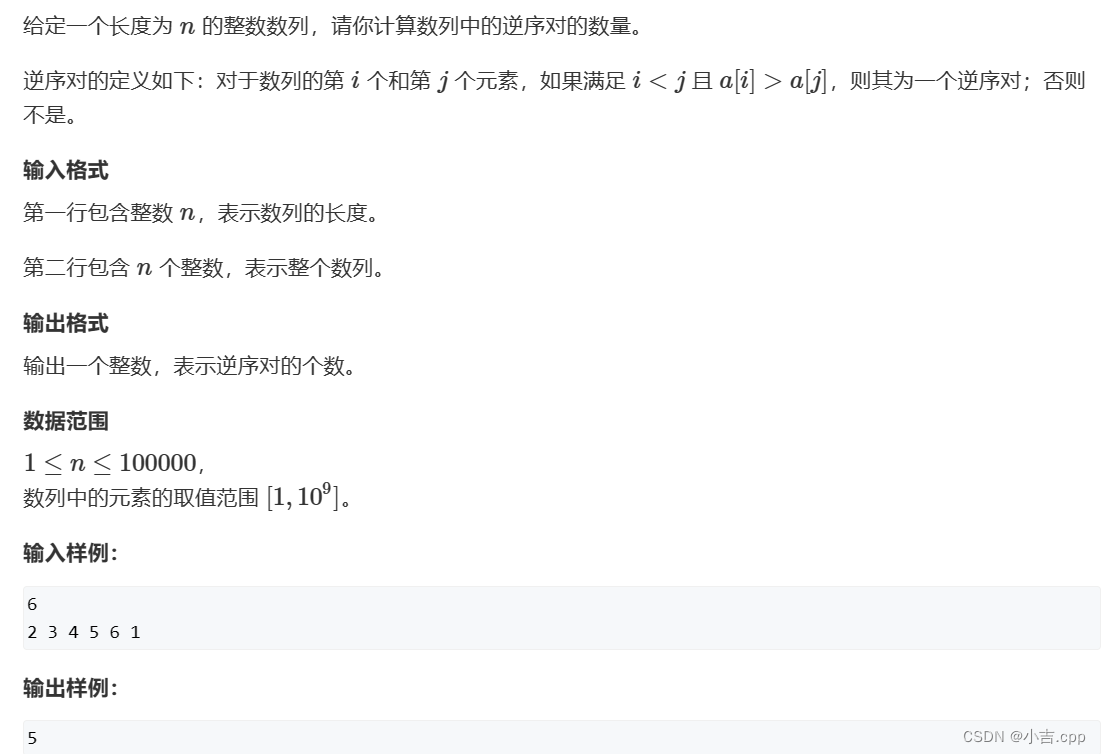
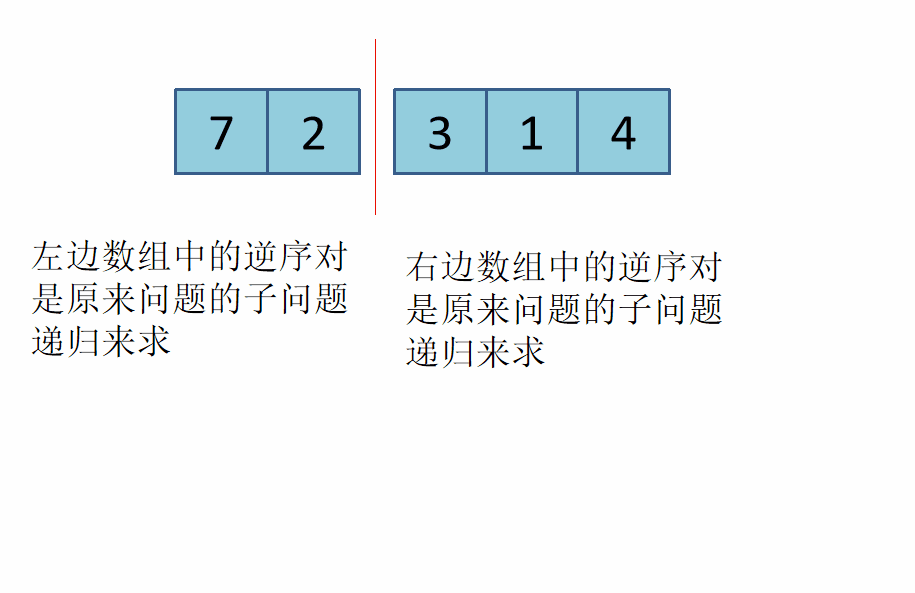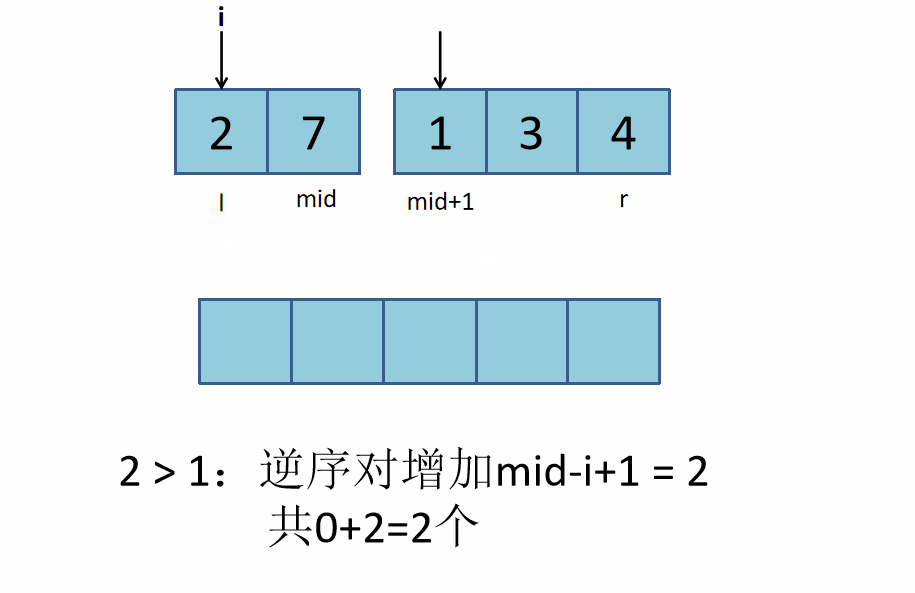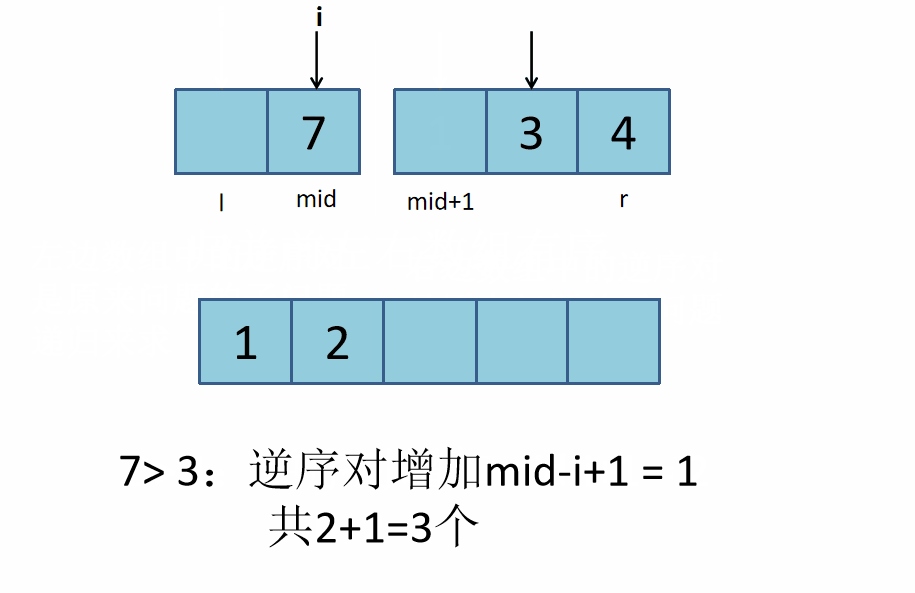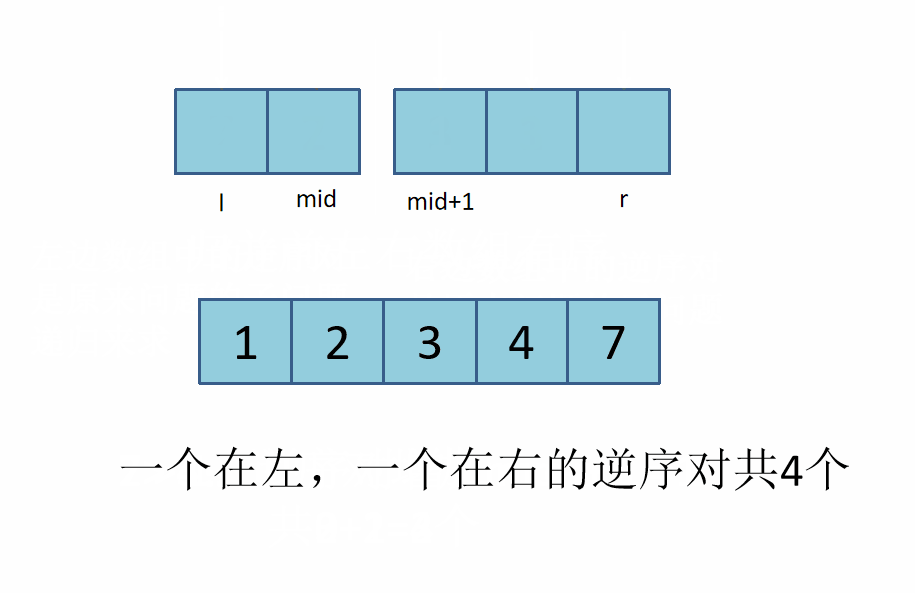
res+=mid-i+1 

#include <iostream>
using namespace std;
const int N = 100010;
int a[N];
int temp[N];

long long find(int a[], int l, int r){

    if(l >= r) return 0;//别忘了截止条件

    int mid = l + (r - l >> 1);
    long long res = 0;
    res += find(a, l, mid);
    res += find(a, mid + 1, r);

    int i = l, j = mid + 1, k = 0;
    while(i <= mid && j <= r){
        if(a[i] <= a[j]) temp[k++] = a[i++];
        else
        {
            temp[k++] = a[j++];
            res += mid - i + 1;
        }
    }
    while(i <= mid) temp[k++] = a[i++];
    while(j <= r) temp[k++] = a[j++];

    for(i = l,k = 0;i <= r;i++)
        a[i] = temp[k++];
    return res;


}

int main(){
    int n;
    cin >> n;
    for(int i = 0; i < n;i++){
        cin >> a[i];
    }
    cout << find(a, 0 ,n - 1);
}

别急，小吉还没有讲完😛

⭐⭐⭐

大家知道为什么是mid = l + (r - l >> 1)而不是mid = l + r >> 1 吗

因为当 l r 都特别大时( l+r ) 的值可能会特别大，可能会爆掉，但是mid = l + (r - l >> 1)就不一定了

⭐⭐⭐

Code over!