1、线性表的概念

线性表是具有相同特性的数据元素的一个有限序列。就像用细线串珠子，一个接着一个串起来。

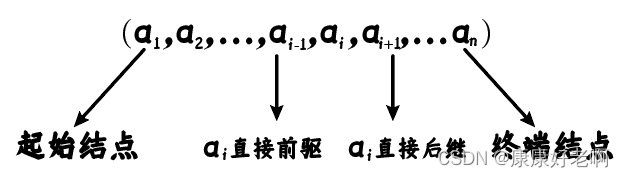
2、线性表的逻辑特征

① 在非空的线性表中有且只有一个开始结点a1，他没有直接前驱，而仅有一个直接后继a2，相当于a1是开头，后面紧跟着连接a2

② 有且仅有一个终端结点a（n），它没有直接后继，而仅有一个直接前驱a（n-1），相当于a（n）是结尾，前面接着a（n-1）

③ 其余结点有且只有一个直接前驱和一个直接后继

线性表的实际应用

1）比如如下一个多项式，要实现加减法
$$f(x)=10x^5+4x^3+7x^2+2x+6$$
可将其转换为
$$R=(p_0,p_1,p_2,\cdot \cdot \cdot ,p_n)$$
每一个p对应一个系数，x指数可以由p的下标来显示

所以多项式的相加可以转换成
$$R=(p_0+q_0,p_1+q_1,p_2+q_2,\cdot \cdot \cdot ,p_n+q_n)$$
2）若我们进一步要实现稀疏多项式的加减法（就是指数相隔比较分散，如果仍像之前那样则会非常占用内存）

于是我们构造如下的线性表：
$$R=((p_0,e_0),(p_1,e_1),(p_2,e_2),\cdot \cdot \cdot ,(p_n,e_n))$$
这样同时将线性表的指数和系数都储存了起来

步骤：

• 创建新数组C

• 指数相同，对应系数相加，若和不为0，则在C线性表中增加一个新项

• 指数不相同，则将指数较小的项复制到C中

• 一个多项式遍历完毕时，将另一个剩余项依次复制到C中即可

此题也可以使用数组，下图是用链表实现示意图

顺序存储结构存在的问题：

1. 存储空间分配不灵活

2. 运算的空间复杂度高

线性表的类型定义

ADT List{
数据对象:D={a(i)|a(i)属于Elemset,(i=1,2,…,n,n≥0)
数据关系:R={<a(i-1),a(i)>|a(i-1),a(i)属于D,(i=2,3,…,n)} //二元关系
基本操作:
InitList(&L);
DestoryList(&L);
ListInsert(&L,i,e);
ListDelete(&L,i,&e);
······
}ADT List

基本操作：

• 线性表初始化：InitList(&L)

操作结果：构造一个空的线性表L

• 线性表销毁：DestoryList(&L)

初始条件：线性表L已经存在

操作结果：销毁线性表L

• 线性表清除：ClearList(&L)

初始条件：线性表L已经存在

操作结果：将线性表L重置为空表

• 线性表清空：ListEmpty(L)

初始条件：线性表L已经存在

操作结果：若线性表L为空表，则返回TRUE;否则返回FALSE

• 线性表长度：ListLength(L)

初始条件：线性表L已经存在

操作结果：返回线性表L中的数据元素个数

• 线性表查找：GetElem(L,i,&e)

初始条件：线性表L已经存在，1≤i≤ListLength(L)

操作结果：用e返回线性表L中第i个数据元素的值

• 线性表比较：LocateElem(L,e,compare())

初始条件：线性表L已经存在，compare()是数据元素的判定函数

操作结果：返回L中第1个与e满足compare()的数据元素的位序。这样的元素不存在则返回值为0

• 线性表前驱求法：PriorElem(L,cur_e,&pre_e)

初始条件：线性表L已经存在

操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_e返回他的前驱，否则操作失败；pre_e无意义。

• 线性表后继求法：NextElem(L,cur_e,&next_e)

初始条件：线性表L已经存在

操作结果：若cur_e是L的数据元素，且不是最后一个，则用next_e返回他的后继，否则操作失败；则next_e无意义。

• 线性表元素插入：ListInsert(&L,i,e)

初始条件：线性表L已经存在，1≤i≤ListLength(L)+1

操作结果：在L的第i个位置之前插入新的数据元素e，L的长度加一

• 线性表元素删除：ListDelete(&L,i,&e)

初始条件：线性表L已经存在，1≤i≤ListLength(L)

操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减一

• 线性表遍历：ListTraverse(&L,visited())

初始条件：线性表L已经存在

操作结果：依次对线性表中每个元素调用visited()