目录

子序列问题

300.最长递增子序列

674.最长连续递增序列

718.最长重复子数组

1143.最长公共子序列

1035.不相交的线

53.最大子序和

编辑距离

392.判断子序列

115.不同的子序列

583.两个字符串的删除操作

72.编辑距离

回文子串

647.回文子串

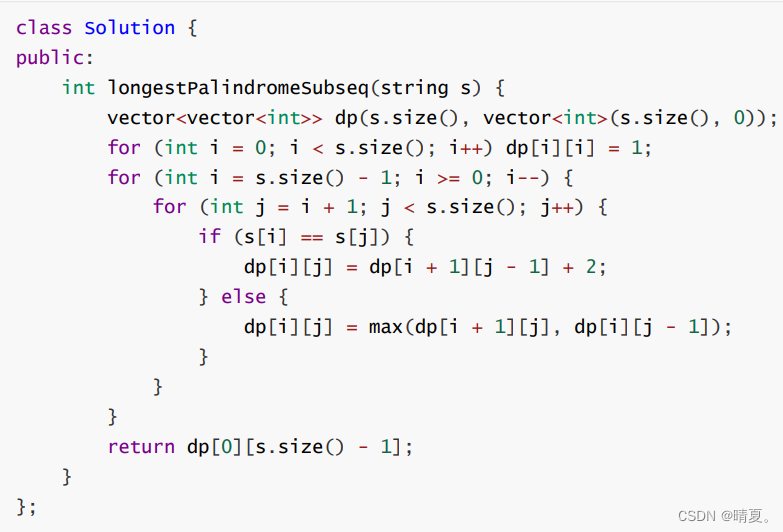
516.最长回文子序列

 698.划分k个相等的子集

子序列问题

本文讲解力扣上所有典型的子序列、编辑距离、回文子串的题目，使用动态规划的解法来做。

300.最长递增子序列

首先我们应该自然而然的想到，题目要我们求的是整个长序列的最长上升子序列的长度，那么也就是说不论多长的一个序列，我们都可以求出这个序列的长度，（也就是子问题）

而事实上，整个序列的值又与其部分子序列是息息相关的。

就例如：比如对于7，它的最长子序列可以来自3，也可以来自5，也可以来自2，

那这三个选择哪个呢？很好想，因为以7结尾的子序列的长度，就等于2、5、3结尾的子序列长度+1即可。

那么我们只要对比以2、5、3作为最后字母的子序列，谁长就行了。

那自然而然就能明白，其实遍历顺序就是，i在外层，当i为2时，j从0、1、2，开始，

对比nums[i]和num[j]，假如nums[i]＞nums[j]，则说明i可以和j的子序列拼接起来

 那么接下来只需要对比i前面的子序列，谁的最大子长度最长即可。

而像这种，求一个整体的数值的问题，可以归结于求其子部分，而子部分又是由前面的子部分所决定，并且还是数组型的，那么就代表着这可以用动态规划！

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int len=nums.size();
        vector<int> dp(len,1);//最长的子序列长度至少是自身，故至少为1

        //int maxLen=0;//错，长度不可能为0
        int maxLen=1;//长度至少也为1
        for(int i=1;i<len;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j])dp[i]=max(dp[i],dp[j]+1);
                
            }
            maxLen=max(maxLen,dp[i]);
        }

        return maxLen;
    }
};

注意特殊案例：

 可能有时候就是卡在一些特殊样例上过不去

674.最长连续递增序列

这题比较简单：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int len=nums.size();
        vector<int> dp(len,1);//最长的子序列长度至少是自身，故至少为1

        int maxLen=1;//长度至少也为1
        for(int i=1;i<len;i++){
            if(nums[i]>nums[i-1])dp[i]=dp[i-1]+1;
            maxLen=max(maxLen,dp[i]);
        }

        return maxLen;

    }
};

718.最长重复子数组

假如对于A的数组，和B的数组，其拥有一个长度为3最大公共子数组。

那么A数组从第i位到第i+2位，和B数组的第j位到第j+2位的应该是相等。

这意味着，A数组的第i位等于B数组的第j位，然后A数组的i+1位等于B数组的j+1位。

这意味着什么呢？这意味着假如我们用dp[i][j]存储A数组的前i位，和B数组的前j位的最大公共子数组，假如第i位和第j位相同，那么此时dp[i][j]=dp[i-1][j-1]+1

意思就是说假如前面已经有两个位置的字符相同了，那么走到这里时，相同的字符就是前面的2加上当前的1了。

(此处的dp[i][j]可以是代表第i位和第j位结尾的字符串所得到的最大长度，也可以是i-1位和j-1位代表的最大长度。

如果是前者，那么二维矩阵中，第0行第0列会代表字符串的第0个字符，并且需要我们自己去初始化第一行第一列。（其实本题的二维矩阵就是下面那种写法的矩阵的右下方罢了：如图红框内容所示：

）

本题该种解法代码如下：

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int len1=nums1.size();
        int len2=nums2.size();
        vector<vector<int>> dp(len1,vector<int>(len2));

        int maxLen=0;
        for(int i=0;i<len1;i++){
            if(nums2[0]==nums1[i]){maxLen=1;dp[i][0]=1;}
        }
        for(int j=0;j<len2;j++){
            if(nums1[0]==nums2[j]){maxLen=1;dp[0][j]=1;}
        }
        for(int i=1;i<len1;i++){
            for(int j=1;j<len2;j++){
                if(nums1[i]==nums2[j])dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=0;
                maxLen=max(maxLen,dp[i][j]);
            }
        }
        return maxLen;
    }
};

如果是后者，则二维矩阵的第0行第0列不代表字符串的第0个，第一行第一列才代表字符串的第一个。此时我们不需要自己去初始化第0行第0列。

对于该dp值的二维数组该如何初始化？注意到我们需要使用到斜上一格，所以第一行第一列需要空出来初始化为0。效果如下：

 说说本题自己遇到的几个坑，首先就是，由于是计算的最长公共子数组的长度，首先就必须要明白，这个子数组必须是连续的！

另一方面，虽然

[1,2]和

[3,1,2]  、[3,1,2,4] 、 [3,1,2,4,5]

虽然和这几个数组的最长公共子数组都是[1,2]没错

但是要明白，本题的dp[i][j]值并不是代表0到i和0到j两个数组的所有子数组中所能达成的最长公共长度！（这也就算为什么返回值不是dp[len1-1][len2-1]了，而是在过程中找最大值（用maxLen来存储）

事实上，dp[i][j]代表的是以i为结尾的数组和以j结尾的数组的最大子数组的长度！（要明白这和上面的差别在于什么！）

可以看到在表格中，第一行只有一个1，（如果是子序列，那么出现了一个1以后，那么这一行后面的dp值只可能变大，不可能变小。 

因为只有这样才能保证dp[i][j]由前面的dp[i-1][j-1]转移过来的时候是连续相等的情况（即子数组而非子序列）

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int len1=nums1.size();
        int len2=nums2.size();
        vector<vector<int> > dp(len1,vector<int> (len2));
        /*//初始化第一列 
        for(int i=0;i<len1;i++){
            if(nums1[i]==nums2[0]){
                for(int k=i;k<len1;k++)dp[k][0]=1;
                break;
            }
        }

        //初始化第一行
        for(int j=0;j<len2;j++){
            if(nums1[0]==nums2[j]){
                for(int k=j;k<len1;k++)dp[0][k]=1;
                break;
            }
        }*/

        int maxLen=0;
        for(int i=0;i<len1;i++){
            if(nums1[i]==nums2[0]){
                maxLen=1;//初始化第一行时此时也有可能最长的长度是1，不要忘了！
                dp[i][0]=1;
            }
        }

        //初始化第一行
        for(int j=0;j<len2;j++){
            if(nums1[0]==nums2[j]){
                dp[0][j]=1;
                maxLen=1;
            }
        }

        for(int i=1;i<len1;i++){
            for(int j=1;j<len2;j++){
                if(nums1[i]==nums2[j]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                //else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//对于子序列是这样
                //else dp[i][j]=0;
                maxLen=max(maxLen,dp[i][j]);
            }
        }



        return maxLen;
    }
};

还有一点容易遗忘的是：

1143.最长公共子序列

注意，本题不要求连续，而前面那题子数组要求连续这意味着dp[i][j]的大小必须是以（i，j）结尾的，而本题不要求连续，这意味着dp[i][j]得到最大值时，不一定是以（i，j）结尾的

意味着dp[i][j]得到最大值时，不一定是以（i，j）结尾的，所以可以是

准确来说当str1[i]和str2[j]不相等时，dp的状态方程应为：

                else dp[i][j]=max(dp[i][j-1],dp[i-1][j],dp[i-1][j-1]);

还应该包含第三个状态，但是左方和上方的数，一定大于等于左上方的数，所以可以忽略这个状态，

class Solution {
public:
    int longestCommonSubsequence(string nums1, string nums2) {
        int len1=nums1.size();
        int len2=nums2.size();
        vector<vector<int> > dp(len1,vector<int> (len2));

        int maxLen=0;

        //初始化第一列 
        for(int i=0;i<len1;i++){
            if(nums1[i]==nums2[0]){
                maxLen=1;
                for(int k=i;k<len1;k++)dp[k][0]=1;
                break;
            }
        }

        //初始化第一行
        for(int j=0;j<len2;j++){
            if(nums1[0]==nums2[j]){
                maxLen=1;
                for(int k=j;k<len2;k++)dp[0][k]=1;
                break;
            }
        }


        for(int i=1;i<len1;i++){
            for(int j=1;j<len2;j++){
                if(nums1[i]==nums2[j]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//对于子序列是这样
                maxLen=max(maxLen,dp[i][j]);
            }
        }

        //return maxLen;
        return dp[len1-1][len2-1];
    }
};

1035.不相交的线

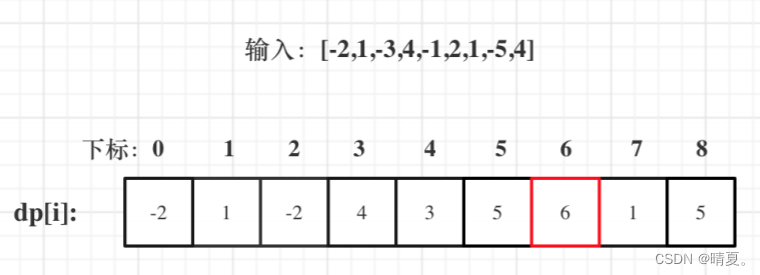
53.最大子序和

编辑距离

392.判断子序列

双指针思路较为简单，此处不在双指针这里过多的赘述。

除此之外，本题与前面的1143.求最长公共子序列的题目十分相像，区别在于1143是求公共长度，本题是求其中一个是否为另外一个的子序列。

那其实很简单，只需要在1143题的代码最下方最终判断一下是否满足公共子序列长度是短的字符串那个的长度即可：

class Solution {
public:
    bool isSubsequence(string nums1, string nums2) {
        int len1=nums1.size();
        int len2=nums2.size();
        if(len1==0)return true;        
        if(len2==0)return false;

        vector<vector<int> > dp(len1,vector<int> (len2));

        int maxLen=0;

        //初始化第一列 
        for(int i=0;i<len1;i++){
            if(nums1[i]==nums2[0]){
                maxLen=1;
                for(int k=i;k<len1;k++)dp[k][0]=1;
                break;
            }
        }

        //初始化第一行
        for(int j=0;j<len2;j++){
            if(nums1[0]==nums2[j]){
                maxLen=1;
                for(int k=j;k<len2;k++)dp[0][k]=1;
                break;
            }
        }


        for(int i=1;i<len1;i++){
            for(int j=1;j<len2;j++){
                if(nums1[i]==nums2[j]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//对于子序列是这样
            }
        }

        return dp[len1-1][len2-1]==len1;
    }
};

可以优化的地方：

由于本题第一个字符串一定比第二个字符串短，

所以如果nums1[i]和nums2[j]不相等，

此时dp值最大的来源肯定是dp[i][j-1]而不会是dp[i-1][j]

因此                                else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
 

可以变为                else dp[i][j]=dp[i][j-1];

可能还得考虑空集这样特殊的例子：

于是乎需要加入这个条件：

115.不同的子序列

（dp[i][j]也可以是代表以i结尾的子串和以j结尾的子串的最大方法数。）

假设不相等，则只能由s[i-2]去和t[j-1]去匹配，因此此时dp[i][j]=dp[i-1][j]

如果相等，那么此时可以由s[i-1]和t[j-1]去匹配，也可以用s[i-2]去和t[j-1]做匹配，也就是多了一种选择。因此此时dp[i][j]=dp[i-1][j]+dp[i-1][j-1]

例如： s：bagg 和 t：bag ，s[3] 和 t[2]是相同的，但是字符串s也可以不⽤s[3]来匹配，即⽤ s[0]s[1]s[2]组成的bag去和t去匹配。而本题是要计算有多少种情况，所以可以由这两种的总方法数加起来。

二次复习时新补充的更便于理解的思路：

比如字符串bag和bxagg

首先就是，我们让i为行，让i代表的是短的那个字符串，然后j代表长的字符串。

我们可以以遍历的顺序来去思考：即一行一行从左到右去遍历 意思就是比如固定短的字符串为：bag，而长的字符串就是从b、bx、bxa、bxag、bxagx、bxagxg去不断加长的过程

另一方面，由于是在的子串j中找i的串，所以j一定大于i。因此，对于二维数组dp值，当j小于i时，dp[i][j]一定为0。

对于两个字符串的第i位和第j位，当i和j不相等时，就说明此时新的那个j的字符是没有用的，例如此时j从4到5，也就是从bxag变成了bxagx，那么此时新增的j对应的字符是x没法匹配上是无用的。于是即使无视这个第j个字符，结果不会变。所以dp值就继承了前面的值，也就是dp[i][j-1]。

但当如果第j个字符相等，即比如此时是bxagxg，此时第j个字符（最后一个）是匹配的，那么，由于是计算的情况数，所以需要把不同的情况累加起来。

首先情况数肯定不会减小，只会增加，增加的数额如何计算呢？那就是，我们都去排除第i个字符和第j个字符，看0到i-1的的字符串和0到j-1的字符串的dp值是多大，加上这个值即可。因此此时

dp[i][j]=dp[i][j-1]+dp[i-1][j-1]

（为什么没有dp[i-1][j]呢？很简单，我觉得就是没有关系

（这也解释了为什么动规的转移方程时不需要考虑dp[i-1][j]

（下面这个解析的i是长字符，j才是短字符串，与我上面的不同

3. dp数组如何初始化

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][0] 和dp[0][j]是 ⼀定要初始化的。

其实此处初始化比较好理解，只要判断第0列和第0行的情况，判断这种情况，t是否是s的子集即可。看下图即可知道怎么初始化：

于是最终代码如下：

583.两个字符串的删除操作

 本题和动态规划：115.不同的⼦序列相⽐，其实就是两个字符串可以都可以删除了，情况虽说复杂⼀ 些，但整体思路是不变的。

动规的dp方程怎么想呢？题目要我们求什么，我们就设定dp值为什么！

要求最小步数，我们就设定dp值为最小步数。

上面的这个+1和+2是哪里来的？就[j]是删除字符得来的，删除第i-1个字符，这个操作就是1次，然后再加上之前的操作次数，即dp值[i-1]

72.编辑距离

其实删除元素还有一种，就是两个字符串各自删除一个当前字符，但是这种情况不如替换字符。因为删两个字符和替换一个字符，最终效果一样。

添加元素的本质上和删除元素是相同的。

回文子串

回文子串的dp值的表达式，遍历顺序，dp推导公式都与其他上面的那些题不是一个类型，因此多开一个板块。

647.回文子串

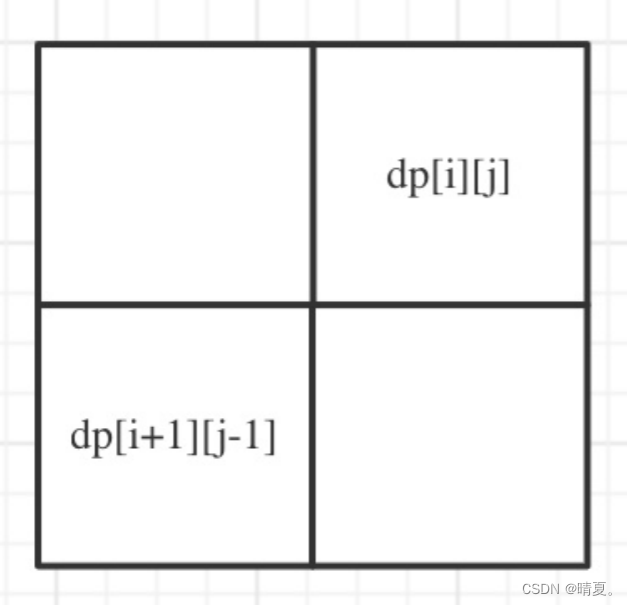
注意，此处的i是从大到小，而j是从小到大。

并且j是要从i出发，因为需要计算j-i的值。

这种循环的实际意义思路就是说：对于字符串abcdefedc来说，先从最后一个结点开始，然后往两边扩散，判断是否是回文，再从倒数第二个结点往中间扩散。对于每个节点往中间扩散。

完整代码如下：

动态规划法复杂度较高，此处看看双指针法。

516.最长回文子序列

  子序列不要求连续！！！

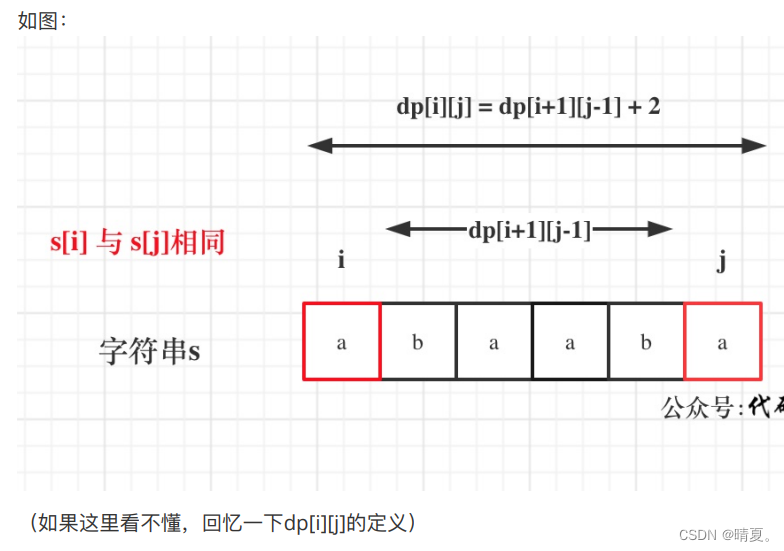
（因为是子序列，并不要求连续，所以可以单独延伸一边，得到一个最大值） 

顺序：从下到上，从左到右

回溯法

 698.划分k个相等的子集

本题的回溯法可以参考这篇文章：

经典回溯算法：集合划分问题「重要更新 🔥🔥🔥」 - 划分为k个相等的子集 - 力扣（LeetCode）

代码：

以前回溯时，我们只需要一个sum即可，比如上面那题分为两个等和子集，实际上只需要考虑一个即可。但是本题有k个，所以我们可以设置k个桶，然后每次dfs时使用一个球，将其放到1~k个桶里面。

对于本题不能使用全局变量findFlag的形式，因为我们一旦找到，即可停止搜索：

​

此外这里还有三个剪枝的方法，具体可以看上面那篇文章讲的很详细。

class Solution {
public:
    int sum=0;
    int target;
    int len;
    vector<int> num;
    vector<int> buckets;

    bool canPartitionKSubsets(vector<int>& nums, int k) {
        num=nums;
        len=nums.size();
        for(auto val:nums)sum+=val;
        if(sum%k!=0)return false;
        buckets.resize(k);
        target=sum/k;
        
        return dfs(0);
    }
    bool dfs(int index){
        if(index==len){
            for(int i=0;i<buckets.size();i++){
                if(buckets[i]!=target)return false;
            }
            return true;
        }

        for(int i=0;i<buckets.size();i++){
            if(buckets[i]+num[index]>target)continue;
            buckets[i]+=num[index];

            if(dfs(index+1))return true;
            buckets[i]-=num[index];
        }
        return false;
    }

};