文章目录
- 参考资料
- 树的前序、中序、后序遍历
- 树的层次遍历
- 回溯与剪枝
- 组合
- 组合总和 III
- 电话号码的字母组合
- 组合总和
- 组合总和 II
参考资料
参考这里面的一些讲解: https://github.com/youngyangyang04/leetcode-master。
树的前序、中序、后序遍历
看完 树的种类 之后,就需要熟悉好树的遍历。
树的前序遍历leetcode:
DFS递归写法很重要,需要重点理解掌握:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res=[]
def dfs(root):
if not root:
return
res.append(root.val)
dfs(root.left)
dfs(root.right)
dfs(root)
return res
在树结构中,DFS可以搞定的,使用栈构成迭代法也是可以搞定的:
# 首先将根节点入栈,然后每次从栈顶取出一个节点,并将其值加入到结果列表中;
# 接着按照右-左-根的顺序将其子节点入栈。
# 由于栈是先进后出的结构,所以弹出左子节点时会优先处理它的子树,从而实现了前序遍历的效果。
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = [root]
while stack:
node = stack.pop()
if not node:
continue
res.append(node.val)
stack.append(node.right)
stack.append(node.left)
return res
迭代法 中序遍历:
# 先将根节点及其所有左子节点入栈,然后每次从栈顶取出一个节点,并将其右子节点入栈,直到栈为空。由于出栈顺序为左-中-右,所以可得到中序遍历的结果
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = []
node = root
while node or stack:
while node:
stack.append(node)
node = node.left
node = stack.pop()
res.append(node.val)
node = node.right
return res
迭代法后序遍历 和 迭代法前序遍历 写法类似:
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
stack = [root]
while stack:
node = stack.pop()
if not node:
continue
res.append(node.val)
stack.append(node.left)
stack.append(node.right)
return res[::-1]
树的层次遍历
可以使用递归法写出:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
res=[]
def dfs(root,depth):
if not root:
return []
if len(res)==depth:res.append([])
res[depth].append(root.val) # depth层的list进行append
dfs(root.left, depth + 1)
dfs(root.right, depth + 1)
dfs(root,0)
return res
也可以使用队列实现:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
result = []
queue = [root]
while queue:
level_size = len(queue)
current_level = []
for i in range(level_size): # 队列当前元素是这一层的Node,全部弹出
node = queue.pop(0)
current_level.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
result.append(current_level)
return result
回溯与剪枝
关于树的算法题目很多,比如求树的深度、节点个数、删除节点等题目,都需要耐心刷完,这里主要关注DFS搜索和BFS搜索,依靠多刷一些题,总结出规律。
按DFS的思维遍历树的节点的时候,意识到DFS的思维是将总问题转为当前可解决的问题与一个子问题,且子问题的解决方式就是总问题,以此达到递归的目的。
按【代码随想录】的题目刷完:
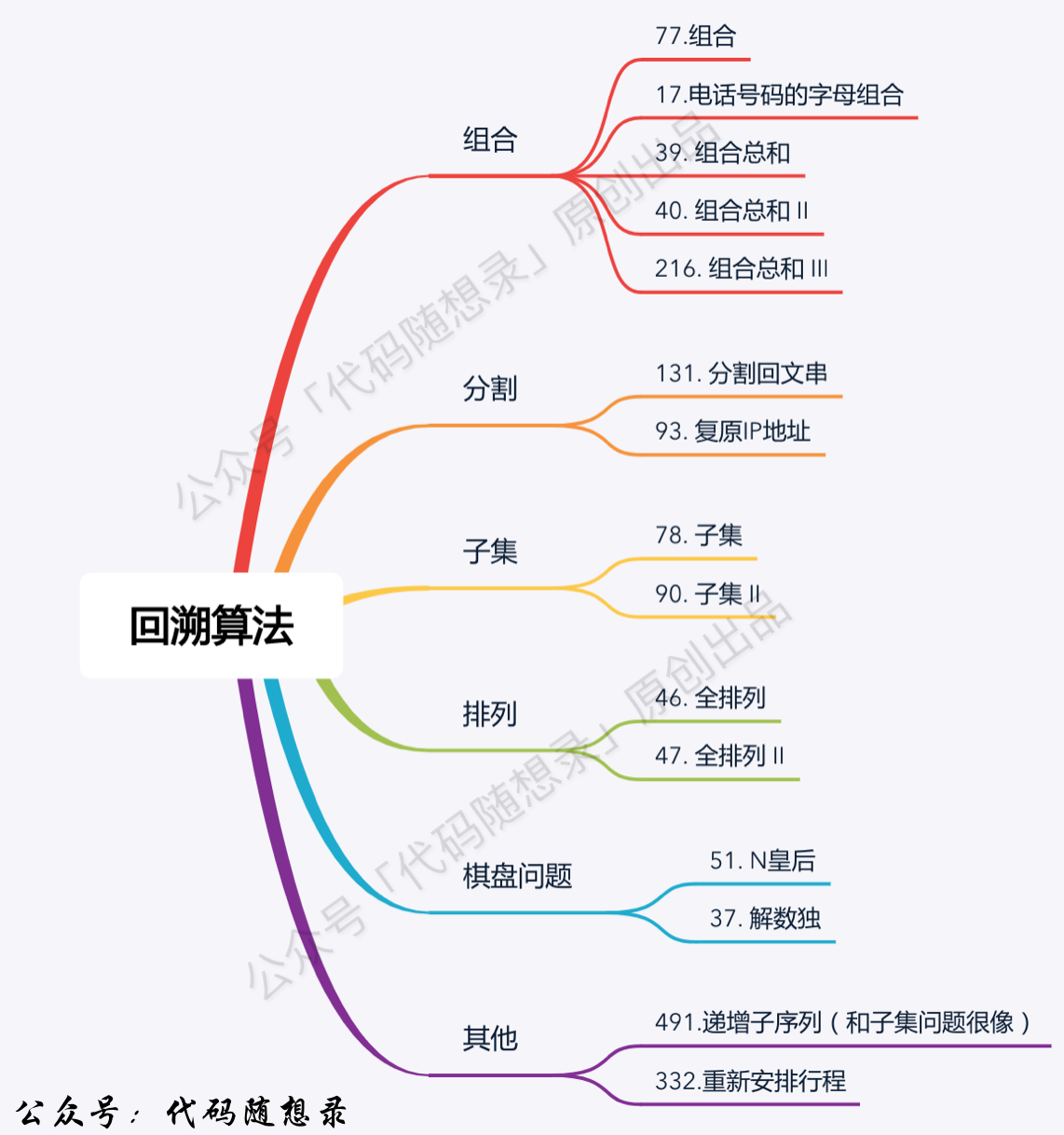
组合
https://leetcode.cn/problems/combinations/:
下面的解法思维会经常性使用,需要思考dfs的传参,思考何时停止条件,思考罗列所有状态:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
nums = list(range(1, n+1))
def backtrack(start, path): # 从哪里开始选元素,这个切入点很重要;当前选了什么元素,这个切入点也重要。
# 如果当前的组合长度等于k,将其加入结果列表
if len(path) == k:
res.append(path[:])
return
# 遍历可选数字,并尝试将其加入组合中
for i in range(start, n):
path.append(nums[i])
backtrack(i+1, path) # 从下个元素开始选
path.pop()
backtrack(0, [])
return res
对于该问题,可以采用一些剪枝策略来优化搜索过程,减少不必要的计算。
一种常见的剪枝策略是 “剪去无法得到 k 个数字的组合”,具体实现为:在递归函数 backtrack 中,当 path 的长度加上从 start 到 n 的数字数量仍然小于 k 时,说明已经无法得到长度为 k 的组合了,此时直接返回即可。
另外,在枚举可选数字时,我们可以限制 i 的上限,以确保最后一个数字被选择时,剩余的数字数量也足够凑成长度为 k 的组合。具体实现为:在 for 循环中,将 i 的上限设置为 n - (k - len(path)) + 1。
剪枝是非常重要的策略,在这里测试的话可以降低时间复杂度7倍。 剪枝的本质就是要思考更多的递归停止条件 。
下面是使用上述两种剪枝策略的代码:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
nums = list(range(1, n+1))
def backtrack(start, path):
# 如果当前的组合长度等于k,将其加入结果列表
if len(path) == k:
res.append(path[:])
return
# 剪枝:无法凑齐k个数字的组合
if len(path) + n - start + 1 < k:
return
# 剪枝:i 的上限
for i in range(start, n - (k - len(path)) + 2):
path.append(nums[i-1])
backtrack(i+1, path)
path.pop()
backtrack(1, [])
return res
组合总和 III
https://leetcode.cn/problems/combination-sum-iii/description/
只用回溯:
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
res = []
nums = [i for i in range(1, 10)]
def dfs(start, path):
if sum(path) == n and len(path) == k:
res.append(path[:])
return
for i in range(start, len(nums)):
path.append(nums[i])
dfs(i + 1, path) # 注意是i+1,不是start+1,start是固定的
path.pop()
dfs(0, [])
return res
加上剪枝:
(1)path总和大于n的直接停止;
(2)i的上限;
class Solution:
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
res = []
nums = [i for i in range(1, 10)]
def dfs(start, path, target):
if target < 0:
return
if len(path) == k and target == 0:
res.append(path[:])
return
# 剪枝:i 的上限
upper = min(8, target) # 最大可选数字
for i in range(start, upper + 1):
if sum(path) + nums[i] > n or len(path) == k:
break
path.append(nums[i])
dfs(i + 1, path, target - nums[i])
path.pop()
dfs(0, [], n)
return res
电话号码的字母组合
https://leetcode.cn/problems/letter-combinations-of-a-phone-number/
Python暴力也很有味道:
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return []
d = {"2": "abc", "3": "def", "4": "ghi", "5": "jkl", "6": "mno", "7": "pqrs", "8": "tuv", "9": "wxyz"}
res = [""]
for i in digits:
res = [x + y for x in res for y in d[i]]
return res
此题的dfs也可以不需要回溯:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return []
d = {"2": "abc", "3": "def", "4": "ghi", "5": "jkl", "6": "mno", "7": "pqrs", "8": "tuv", "9": "wxyz"}
res = []
def dfs(start, path): # 得益于Python的字符串加法,可以把当前字符串带入到下一次dfs,不用回溯记忆
if len(path) == len(digits):
res.append(path)
return
for i in range(start, len(digits)): # 从start开始,因为start之前的已经处理过了s
for j in d[digits[i]]: # 选某一个字母
dfs(i + 1, path + j)
dfs(0, "")
return res
下面是回溯法的思路:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
if not digits:
return list()
phoneMap = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz",
}
def backtrack(index: int):
if index == len(digits):
combinations.append("".join(combination))
return
digit = digits[index]
for letter in phoneMap[digit]:
combination.append(letter)
backtrack(index + 1)
combination.pop()
combination = list()
combinations = list()
backtrack(0)
return combinations
组合总和
https://leetcode.cn/problems/combination-sum/description/
dfs:
# 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
# candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
def dfs(candidates, target, path):
if target < 0:
return
if target == 0:
res.append(path)
return
print(candidates)
for i in range(len(candidates)):
dfs(candidates[i:], target - candidates[i], path + [candidates[i]]) # 传入的还是全部的备选
dfs(candidates, target, [])
return res
回溯法:
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
def dfs(candidates, begin, path, target):
if target == 0:
result.append(path[:])
return
if target < 0:
return
for i in range(begin, len(candidates)):
path.append(candidates[i])
dfs(candidates, i, path, target-candidates[i])
path.pop()
dfs(candidates, 0, [], target)
return result
组合总和 II
https://leetcode.cn/problems/combination-sum-ii/description/
dfs:
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
def dfs(start, target, path):
if target == 0:
res.append(path)
return
for i in range(start, len(candidates)):
if i > start and candidates[i] == candidates[i-1]:
continue
if candidates[i] > target:
break
dfs(i+1, target-candidates[i], path+[candidates[i]])
candidates.sort()
res = []
dfs(0, target, [])
return res