电子技术——功率耗散
如今许多集成电路系统都是电池供电的,对于功率耗散限制很严格。其他高性能电路,例如计算机服务器机房产品,有着严格的热耗散功率限制。所以,减小IC中的功率耗散变成了IC设计中最重要的挑战性的设计。
本节,我们介绍数字CMOS电路中热耗散的来源以及减小热耗散方法。
热耗散来源
让我们考虑一个CMOS反相器,无论是当 v I v_I vI 为高电平或者是低电平,其都不会产生功率耗散。而对于其他反相器,则会产生大约 V D D 2 / R V_{DD}^2 / R VDD2/R 并且数值可能很大。我们称不发生在开关过程中产生的功率耗散为 静态功率耗散 。
然而,我们知道,在CMOS反相器存在许多寄生电容,当反相器从一个状态切换到另一个状态的时候,此时需要对电容进行充放电,因此会存在充放电电流,这会导致功率耗散。我们称发生在开关过程中的功率耗散为 动态功率耗散 。
考虑当输入 v I v_I vI 为高电平的时候,此时PUN闭合,而PDN打开,其电路等效为:
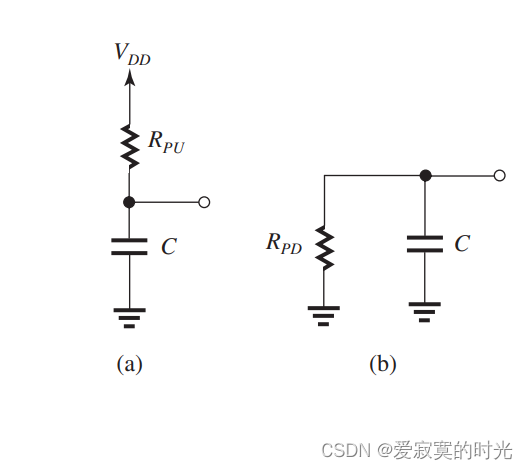
此时需要给电容充电,直到电容电压为
V
D
D
V_{DD}
VDD 。记
i
D
(
t
)
i_D(t)
iD(t) 为
V
D
D
V_{DD}
VDD 提供的充电电流,则瞬间功率为:
p D D ( t ) = V D D i D ( t ) p_{DD}(t) = V_{DD}i_D(t) pDD(t)=VDDiD(t)
假设充电周期为 T c T_c Tc ,我们可以积分求得在充电过程中的总能量:
E D D = ∫ 0 T c V D D i D ( t ) d t = V D D ∫ 0 T c i D ( t ) d t = V D D Q E_{DD} = \int_{0}^{T_c} V_{DD} i_D(t) dt = V_{DD}\int_{0}^{T_c} i_D(t) dt = V_{DD}Q EDD=∫0TcVDDiD(t)dt=VDD∫0TciD(t)dt=VDDQ
这里 Q Q Q 指的是充电过程中总的充电电荷,我们假设0时刻的时候电容电荷量为零,这可以由电容公式导出:
Q = C V D D Q = CV_{DD} Q=CVDD
因此:
E D D = C V D D 2 E_{DD} = CV_{DD}^2 EDD=CVDD2
我们知道,在充电结束后,有一部分能量转换为电场能量储存在电容器中,平行电场能量为:
E s = 1 2 C V D D 2 E_s = \frac{1}{2}CV_{DD}^2 Es=21CVDD2
则耗散功率为:
E d = E D D − E s = 1 2 C V D D 2 E_d = E_{DD} - E_s = \frac{1}{2}CV_{DD}^2 Ed=EDD−Es=21CVDD2
这些能量由电路中的电阻消耗,变成热量耗散。
同样的,当 v I v_I vI 输入为低电平的时候,同样在放电过程中存在耗散能量:
E d = 1 2 C V D D 2 E_d = \frac{1}{2}CV_{DD}^2 Ed=21CVDD2
CMOS反相器中一个周期包括充放电两个过程,因此一个周期内的能量耗散为:
E d / c y c l e = C V D D 2 E_d / cycle = CV_{DD}^2 Ed/cycle=CVDD2
若反相器的频率为 f f f 赫兹,那么动态功率耗散定义为:
P d y n = f C V D D 2 P_{dyn} = fCV_{DD}^2 Pdyn=fCVDD2
这个式子表示减小 C C C 可以减小功率耗散。但是实际上电容 C C C 绝大部分由晶体管本身决定很难大幅度降低。或者我们可以降低 V D D V_{DD} VDD 来减小功率耗散,这也是半导体工艺发展的一个重要的驱动力,例如 0.5um 的工艺需要使用5V的电压,而 0.13um 的工艺只需要1.2V。
最后,因为 P d y n P_{dyn} Pdyn 正比于 f f f ,另一种方法可以通过降频的方式来减小功率耗散,但是这并不是以很好的主意,特别是在如今高速数字系统的发展。例如,在一个具有 27.5 亿个晶体管频率为 5GHz 的数字IC的热功率能达到超过 100W 。
除此之外,还存在一种动态电流会产生热功率消耗,当反相器状态改变的时候,会存在一段时间,两个MOS均会导通电流,如图:
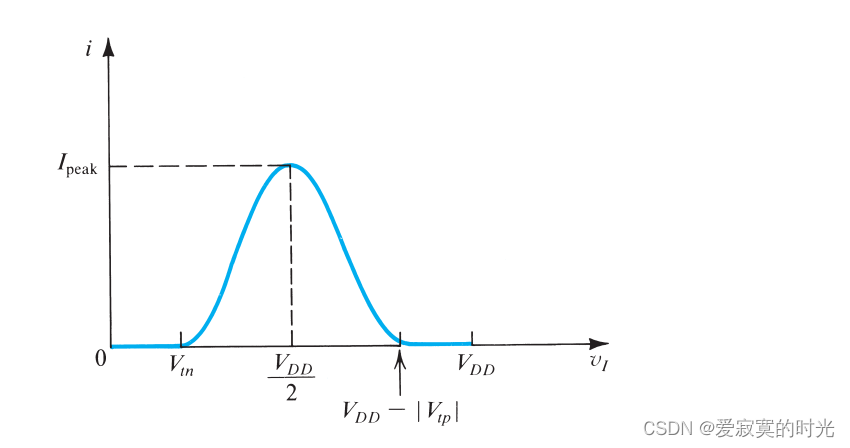
我们发现当输入为
v
I
=
V
M
=
V
D
D
2
v_I = V_M = \frac{V_{DD}}{2}
vI=VM=2VDD 的时候,此时这种电流达到峰值,同时两个MOS都处于饱和区,峰值电流为:
I p = 1 2 μ n C o x ( W / L ) n ( V D D 2 − V t n ) 2 I_p = \frac{1}{2} \mu_n C_{ox} (W/L)_n (\frac{V_{DD}}{2} - V_{tn})^2 Ip=21μnCox(W/L)n(2VDD−Vtn)2
因为数字系统的上升和下降频率的速度都非常快,所以这种功率耗散要远小于电容耗散的功率,因此这种功率耗散通常忽略不计。
功率延迟和能量延迟积
我们最终希望的是高速低功耗系统,但是不幸的是,这两个因素直接存在冲突。若设计师想通过降低 V D D V_{DD} VDD 来减小功耗,这同样会降低反相器的电流驱动能力,进而导致 t P t_P tP 的增加。 功率-延迟积 是评价这两种因素的指标:
P D P ≡ P D t P PDP \equiv P_D t_P PDP≡PDtP
这里 P D P_D PD 是反相器的耗散功率, P D P PDP PDP 具有能量量纲。说明 P D P PDP PDP 越小,则该数字系统越好。
对于CMOS反相器来说,静态耗散功率为零,功率只有 P d y n P_{dyn} Pdyn ,因此:
P D P = f C V D D 2 t P PDP = fCV_{DD}^2 t_P PDP=fCVDD2tP
若 t P t_P tP 达到理论最大最大值 t P = 1 2 f t_P = \frac{1}{2f} tP=2f1 则:
P D P = 1 2 C V D D 2 PDP = \frac{1}{2} CV_{DD}^2 PDP=21CVDD2
注意到 1 2 C V D D 2 \frac{1}{2} CV_{DD}^2 21CVDD2 是给电容充电和放电过程中的能量消耗,因此PDP存在一个合理的物理解释:PDP是反相器输出的过渡阶段的能量消耗。
但是PDP并不是一个评判系统性能的一个总体性指标,因为如果设计师想降低 P D P PDP PDP 可以降低 V D D V_{DD} VDD 来实现,但是 t P t_P tP 同时会增加,但是PDP没有包含 t P t_P tP 的信息。所以我们定义 能量-延迟积EDP 为:
E D P ≡ Energy per transition × t P = 1 2 C V D D 2 t P EDP \equiv \text{Energy per transition} \times t_P = \frac{1}{2} CV_{DD}^2t_P EDP≡Energy per transition×tP=21CVDD2tP