以下我们将介绍两个密切相关的损失函数，它们可以用于神经网络，因此也可用于基于 TensorFlow 2 的 Keras，它们的行为类似于支持向量机生成分类决策边界的方式：铰链损失和平方铰链损失。

阅读本教程后，您将了解...

• 铰链损失和平方铰链损失的工作原理。
• 两者之间有什么区别。
• 如何使用基于 TensorFlow 2 的 Keras 实现铰链损失和平方铰链损失。

让我们开始吧！

二、什么是铰链损失？

在我们关于损失函数的博客文章中，我们对铰链损失的定义如下（维基百科，2011 年）：

数学可能看起来很可怕，但上述公式的解释实际上非常简单。

在训练机器学习模型时，您可以有效地转发数据，生成预测，然后将其与实际目标进行比较以生成一些成本值，即损失值。在使用铰链损失公式生成该值的情况下，将预测 （y） 与预测 （t） 的实际目标进行比较，从 1 中减去该值，然后计算 0 与先前计算结果之间的最大值。

对于每个样本，我们的目标变量 t 为 +1 或 -1。

这意味着：

• 当 t = y 时，例如 t = y = 1，损失为 max（0， 1–1） = max（0， 0） = 0 — 或完全。
• 当 t 与 y 相差很大时，比如 t = 1 而 y = -1，损失是 max（0， 2） = 2。
• 当 t 不完全正确，但只是略微偏离时（例如 t = 1 而 y = 0.9，损失将为 max（0， 0.1） = 0.1）。

如果目标是 +1，则如下所示 — 对于所有目标 >= 1，损失为零（预测正确甚至过度正确），而当预测不正确时，损失会增加。

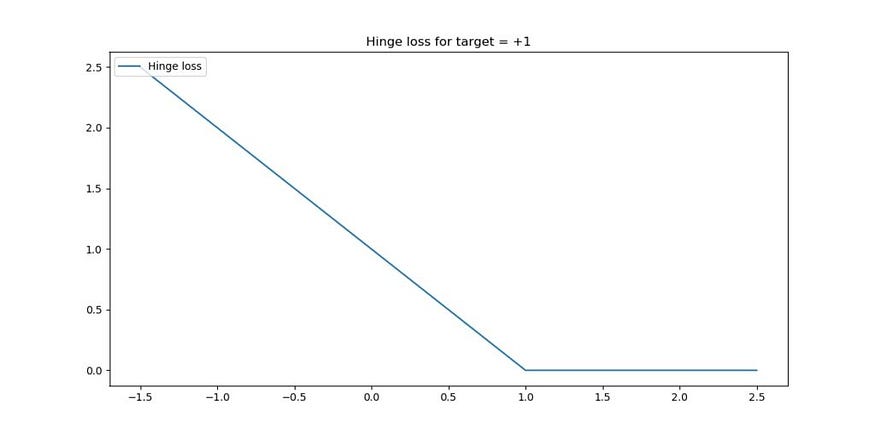
实际上，铰链损失将尝试最大化在机器学习问题中必须区分的两组之间的决策边界。在这一点上，它类似于支持向量机的工作方式，但也有所不同（例如，在 Keras 中，由于铰链丢失，没有支持向量这样的东西）。

三、什么是平方铰链损失？

假设您需要绘制一个非常精细的决策边界。在这种情况下，您希望比较小的错误更显著地 “惩罚” 较大的错误。平方铰链损失可能就是你正在寻找的，特别是当你已经考虑过机器学习问题的铰链损失函数时。

平方铰链损失只不过是铰链的 max（...） 函数输出的平方。它生成了一个损失函数，如上图所示，与常规铰链损失进行比较。

如您所见，与传统铰链相比，较大的错误受到的惩罚更多，而较小的错误受到的惩罚更少。

此外，特别是在上述情况下，在 target = +1.0 附近（如果你的目标是 -1.0，它也适用），传统铰链损失的损失函数表现得相对不平滑，就像 ReLU 激活函数在 x = 0 附近所做的那样。尽管可能性很小，但它可能会影响模型的优化方式，因为损失情况并不平坦。使用方形铰链时，函数是平滑的，但它对较大的误差（异常值）更敏感。

所以，请谨慎选择！

三、实施：关于数据集

现在我们知道了什么是铰链损失和平方铰链损失，我们可以开始实际的实现了。我们必须先实现并讨论我们的数据集，以便能够创建模型。

在我们开始之前，最好在你机器上的某个文件夹中创建一个文件（例如 hinge-loss.py ）。然后，我们可以从添加必要的软件依赖项开始：

'''
  Keras model discussing Hinge loss.
'''
import tensorflow.keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_circles
from mlxtend.plotting import plot_decision_regions

首先，我们需要 Keras 深度学习框架，它使我们能够相对容易地创建神经网络架构。从 Keras 中，我们将导入 Sequential API 和 Dense 层（表示密集连接的层，或者当人们在演示文稿中使用神经网络时经常看到的类似 MLP 的层）。

然后，我们从 Matplotlib 导入 PyPlot API 进行可视化，从 Numpy 导入数字处理，make_circles从 Scikit-learn 导入 Mlxtend 以生成今天的数据集，并从 Mlxtend 导入模型决策边界。

3.1 运行它所需的条件

因此，这就是运行今天代码所需的内容：

• Python，最好是 3.12+
• TensorFlow 2、
• 马特普洛特库
• Numpy
• Scikit-learn
• Mlxtend 公司

…最好在 Anaconda 环境中，以便您的包与其他 Python 包隔离运行。

3.2 生成数据

如图所示，我们现在可以生成数据，用于演示铰链损失和平方铰链损失的工作原理。我们今天生成自己的数据集，因为它使我们能够完全专注于损失函数，而不是清理数据。当然，您也可以将此博客文章中的见解应用于其他真实的数据集。

我们现在指定一些配置选项：

# Configuration options
num_samples_total = 1000
training_split = 250

简而言之，这些参数指定了总共生成了多少样本，以及从训练集中分割了多少样本以形成测试集。使用此配置，我们生成了 1000 个样本，其中 750 个是训练数据，250 个是测试数据。稍后您将看到 750 个训练样本随后被拆分为真实训练数据和验证数据。

接下来，我们实际生成数据：

# Generate data
X, targets = make_circles(n_samples = num_samples_total, factor=0.1)
targets[np.where(targets == 0)] = -1
X_training = X[training_split:, :]
X_testing = X[:training_split, :]
Targets_training = targets[training_split:]
Targets_testing = targets[:training_split]

我们首先为机器学习问题调用make_circles生成 num_samples_total（配置为 1,000）。make_circles 正如它所建议的：它生成两个圆圈，一个较大的圆圈和一个较小的圆圈，它们是可分离的 - 因此非常适合机器学习博客文章。该参数应在 0 < ​​​​​​​factor < 1 的范围内，用于确定圆彼此之间的接近程度。值越低，圆圈之间的距离越远。

接下来，我们将所有零目标转换为 -1。为什么？非常简单：make_circles生成 0 或 1 的目标数据，这在这些情况下非常常见。在简单的英语中，0 或 1 是“较大的圆圈”或“较小的圆圈”，但由于 Keras 中的目标是数字，因此它们是 0 和 1。

Hinge loss铰链损失不适用于 0 和 1。相反，目标必须为 +1 或 -1。因此，我们必须将所有零目标转换为 -1 以支持 。

最后，我们将数据拆分为特征向量（X 变量）和目标的训练和测试数据。

3.3 可视化数据

我们现在还可以可视化数据，以了解我们刚刚所做的工作：

# Generate scatter plot for training data
plt.scatter(X_training[:,0], X_training[:,1])
plt.title('Nonlinear data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()

这看起来如下：

如您所见，我们生成了两个由单个数据点组成的圆圈：一个大的和一个较小的。这些是完全可分的，尽管不是线性的。

（使用传统的 SVM 时，必须执行内核技巧才能使数据在内核空间中线性可分。对于神经网络，这不是什么问题，因为各层是非线性激活的。

四、在 TensorFlow 2/Keras 中实现铰链损失和平方铰链损失

现在我们已经对数据集有了感觉，我们实际上可以tensorflow.keras实现一个模型，该模型利用铰链损失，在另一次运行中，利用平方铰链损失，以向您展示它是如何工作的。

4.1 模型配置

像往常一样，我们首先通过将其添加到我们的代码中来定义一些用于模型配置的变量：

# Set the input shape
feature_vector_shape = len(X_training[0])
input_shape = (feature_vector_shape,)
loss_function_used = 'hinge'
print(f'Feature shape: {input_shape}')

我们将特征向量的形状设置为训练集中第一个样本的长度。如果此样本的长度为 3，则表示特征向量中有三个特征。由于数组只是一维的，因此形状将是长度为 3 的一维向量。由于我们的训练集包含数据点的 X 和 Y 值，因此我们的input_shape 为（2，）。

显然，我们使用hinge 作为损失函数。使用平方铰链损失也可以通过简单地将​​​​​​​hinge更改为squared_hinge 来实现。这取决于你！​​​​​​​

4.2 模型架构

接下来，我们定义模型的架构：

# Create the model
model = Sequential()
model.add(Dense(4, input_shape=input_shape, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(2, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='tanh'))

我们使用 Keras Sequential API，它使我们能够轻松堆叠多个层。与其他博客文章相反，例如我们创建用于分类或回归的 MLP 的博客文章，我决定添加三个层而不是两个层。这样做是因为数据集稍微复杂一些：决策边界不能表示为一条线，而必须是一个圆圈，将较小的边界与较大的边界分隔开来。因此，我认为，多一点处理数据的能力会很有用。

这些层使用 Rectified Linear Unit 或 ReLU 激活，但最后一个层除外，它通过 Tanh 激活。我选择 ReLU 是因为它实际上是标准激活函数，并且需要最少的计算资源，而不会影响预测性能。我选择 Tanh 是因为预测的生成方式：考虑到铰链损失的运作方式，它们最终应该在 [-1， +1] 范围内（还记得为什么我们必须将生成的目标从 0 转换为负 1 吗？

Tanh 正是这样做的 — 将线性值转换为接近 [-1， +1] 的范围，即 （-1， +1） — 实际值不包括在这里，但这并不重要。它看起来像这样：

ReLU 激活层的内核使用 He uniform init 而不是 Glorot init 进行初始化，因为这种方法在数学上效果更好。

信息最终会转换为一个预测：目标。因此，最后一层有一个神经元。中间的神经元较少，以便刺激模型在前馈过程中生成更抽象的信息表示。

4.3 超参数配置和开始模型训练

现在我们知道了我们将使用什么架构，我们可以执行超参数配置。

# Configure the model and start training
model.compile(loss=loss_function_used, optimizer=tensorflow.keras.optimizers.Adam(lr=0.03), metrics=['accuracy'])

使用的损失函数hinge实际上是 loss。我们使用 Adam 进行优化，并手动将学习率配置为 0.03，因为初步实验表明，默认学习率不足以多次学习决策边界。就您而言，您可能还必须根据学习率进行随机调整;您可以在那里进行配置。作为一项额外的指标，我们纳入了准确性，因为人类可以更好地解释它。

现在是实际的训练过程：

history = model.fit(X_training, Targets_training, epochs=30, batch_size=5, verbose=1, validation_split=0.2)

我们将训练数据 （ X_training和Targets_training ） 拟合到模型架构，并允许它优化 30 个 epoch 或迭代。在一个 epoch 期间通过网络向前馈送的每个批次都包含 5 个样品，这使其能够从准确的梯度中受益，而不会损失太多时间和/或资源，因为这些时间和/或资源会随着批次大小的减小而增加。详细模式设置为 1 （'True'），以便在训练过程中输出所有内容，这有助于您理解。如前所述，我们将训练数据分为真实训练数据和验证数据：20% 的训练数据用于验证。

因此，在生成的 1,000 个样本中，250 个用于测试，600 个用于训练，150 个用于验证 （600 + 150 + 250 = 1000）。

4.4 测试和可视化模型性能

我们将拟合（训练）过程的结果存储到一个history对象中，这使我们能够实际可视化跨 epoch 的模型性能。但首先，我们添加代码来测试模型的泛化能力：

# Test the model after training
test_results = model.evaluate(X_testing, Targets_testing, verbose=1)
print(f'Test results - Loss: {test_results[0]} - Accuracy: {test_results[1]*100}%')

然后，我们根据测试数据绘制决策边界图：

# Plot decision boundary
plot_decision_regions(X_testing, Targets_testing, clf=model, legend=2)
plt.show()

最终，训练过程的可视化：

# Visualize training process
plt.plot(history.history['loss'], label='Hinge loss (testing data)')
plt.plot(history.history['val_loss'], label='Hinge loss (validation data)')
plt.title('Hinge loss for circles')
plt.ylabel('Hinge loss value')
plt.yscale('log')
plt.xlabel('No. epoch')
plt.legend(loc="upper left")
plt.show()

（使用对数刻度是因为损耗在第一个 epoch 期间显着下降，如果线性缩放，则会使图像失真。

4.5 结果：模型性能

现在，如果您到目前为止已经按照该过程进行作，那么您有一个名为hinge-loss.py的文件 ​​​​​​​cd..打开可以访问您的设置的终端py文件所在位置，hinge-loss.py到存储您的文件夹并执行python hinge-loss.py .然后，训练过程应开始。 

这些是结果。

4.6 铰链损失

对于铰链损失，我们毫不奇怪地发现验证准确率立即达到 100%。这确实不足为奇，因为数据集的可分离性非常好（圆之间的距离很大），该模型非常能够解释相对复杂的数据，并且设置了相对激进的学习率。这是使用对数刻度的训练过程的可视化：

决策边界：

或者以纯文本形式：

<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424">Epoch 1/30
600/600 [==============================] - 1s 1ms/step - loss: 0.4317 - accuracy: 0.6083 - val_loss: 0.0584 - val_accuracy: 1.0000
Epoch 2/30
600/600 [==============================] - 0s 682us/step - loss: 0.0281 - accuracy: 1.0000 - val_loss: 0.0124 - val_accuracy: 1.0000
Epoch 3/30
600/600 [==============================] - 0s 688us/step - loss: 0.0097 - accuracy: 1.0000 - val_loss: 0.0062 - val_accuracy: 1.0000
Epoch 4/30
600/600 [==============================] - 0s 693us/step - loss: 0.0054 - accuracy: 1.0000 - val_loss: 0.0038 - val_accuracy: 1.0000
Epoch 5/30
600/600 [==============================] - 0s 707us/step - loss: 0.0036 - accuracy: 1.0000 - val_loss: 0.0027 - val_accuracy: 1.0000
Epoch 6/30
600/600 [==============================] - 0s 692us/step - loss: 0.0026 - accuracy: 1.0000 - val_loss: 0.0020 - val_accuracy: 1.0000
Epoch 7/30
600/600 [==============================] - 0s 747us/step - loss: 0.0019 - accuracy: 1.0000 - val_loss: 0.0015 - val_accuracy: 1.0000
Epoch 8/30
600/600 [==============================] - 0s 717us/step - loss: 0.0015 - accuracy: 1.0000 - val_loss: 0.0012 - val_accuracy: 1.0000
Epoch 9/30
600/600 [==============================] - 0s 735us/step - loss: 0.0012 - accuracy: 1.0000 - val_loss: 0.0010 - val_accuracy: 1.0000
Epoch 10/30
600/600 [==============================] - 0s 737us/step - loss: 0.0010 - accuracy: 1.0000 - val_loss: 8.4231e-04 - val_accuracy: 1.0000
Epoch 11/30
600/600 [==============================] - 0s 720us/step - loss: 8.6515e-04 - accuracy: 1.0000 - val_loss: 7.1493e-04 - val_accuracy: 1.0000
Epoch 12/30
600/600 [==============================] - 0s 786us/step - loss: 7.3818e-04 - accuracy: 1.0000 - val_loss: 6.1438e-04 - val_accuracy: 1.0000
Epoch 13/30
600/600 [==============================] - 0s 732us/step - loss: 6.3710e-04 - accuracy: 1.0000 - val_loss: 5.3248e-04 - val_accuracy: 1.0000
Epoch 14/30
600/600 [==============================] - 0s 703us/step - loss: 5.5483e-04 - accuracy: 1.0000 - val_loss: 4.6540e-04 - val_accuracy: 1.0000
Epoch 15/30
600/600 [==============================] - 0s 728us/step - loss: 4.8701e-04 - accuracy: 1.0000 - val_loss: 4.1065e-04 - val_accuracy: 1.0000
Epoch 16/30
600/600 [==============================] - 0s 732us/step - loss: 4.3043e-04 - accuracy: 1.0000 - val_loss: 3.6310e-04 - val_accuracy: 1.0000
Epoch 17/30
600/600 [==============================] - 0s 733us/step - loss: 3.8266e-04 - accuracy: 1.0000 - val_loss: 3.2392e-04 - val_accuracy: 1.0000
Epoch 18/30
600/600 [==============================] - 0s 782us/step - loss: 3.4199e-04 - accuracy: 1.0000 - val_loss: 2.9011e-04 - val_accuracy: 1.0000
Epoch 19/30
600/600 [==============================] - 0s 755us/step - loss: 3.0694e-04 - accuracy: 1.0000 - val_loss: 2.6136e-04 - val_accuracy: 1.0000
Epoch 20/30
600/600 [==============================] - 0s 768us/step - loss: 2.7671e-04 - accuracy: 1.0000 - val_loss: 2.3608e-04 - val_accuracy: 1.0000
Epoch 21/30
600/600 [==============================] - 0s 778us/step - loss: 2.5032e-04 - accuracy: 1.0000 - val_loss: 2.1384e-04 - val_accuracy: 1.0000
Epoch 22/30
600/600 [==============================] - 0s 725us/step - loss: 2.2715e-04 - accuracy: 1.0000 - val_loss: 1.9442e-04 - val_accuracy: 1.0000
Epoch 23/30
600/600 [==============================] - 0s 728us/step - loss: 2.0676e-04 - accuracy: 1.0000 - val_loss: 1.7737e-04 - val_accuracy: 1.0000
Epoch 24/30
600/600 [==============================] - 0s 680us/step - loss: 1.8870e-04 - accuracy: 1.0000 - val_loss: 1.6208e-04 - val_accuracy: 1.0000
Epoch 25/30
600/600 [==============================] - 0s 738us/step - loss: 1.7264e-04 - accuracy: 1.0000 - val_loss: 1.4832e-04 - val_accuracy: 1.0000
Epoch 26/30
600/600 [==============================] - 0s 702us/step - loss: 1.5826e-04 - accuracy: 1.0000 - val_loss: 1.3628e-04 - val_accuracy: 1.0000
Epoch 27/30
600/600 [==============================] - 0s 802us/step - loss: 1.4534e-04 - accuracy: 1.0000 - val_loss: 1.2523e-04 - val_accuracy: 1.0000
Epoch 28/30
600/600 [==============================] - 0s 738us/step - loss: 1.3374e-04 - accuracy: 1.0000 - val_loss: 1.1538e-04 - val_accuracy: 1.0000
Epoch 29/30
600/600 [==============================] - 0s 762us/step - loss: 1.2326e-04 - accuracy: 1.0000 - val_loss: 1.0645e-04 - val_accuracy: 1.0000
Epoch 30/30
600/600 [==============================] - 0s 742us/step - loss: 1.1379e-04 - accuracy: 1.0000 - val_loss: 9.8244e-05 - val_accuracy: 1.0000
250/250 [==============================] - 0s 52us/step
Test results - Loss: 0.0001128034592838958 - Accuracy: 100.0%</span></span></span></span>

我们可以看到，验证损失仍然随着训练损失而减少，因此模型还没有过拟合。

原因是什么？简单。我的假设是，发生这种情况是因为训练集和验证集中的数据都是完全可分离的。决策边界非常清晰。

4.7 平方铰链损失

通过loss_function_used更改为squared_hinge， 我们现在可以向你显示方形铰链的结果：​​​​​​​

loss_function_used = 'squared_hinge'

从视觉上看，它如下所示：

再次是纯文本：

<span style="color:rgba(0, 0, 0, 0.8)"><span style="background-color:#ffffff"><span style="background-color:#f9f9f9"><span style="color:#242424">Epoch 1/30
600/600 [==============================] - 1s 1ms/step - loss: 0.2361 - accuracy: 0.7117 - val_loss: 0.0158 - val_accuracy: 1.0000
Epoch 2/30
600/600 [==============================] - 0s 718us/step - loss: 0.0087 - accuracy: 1.0000 - val_loss: 0.0050 - val_accuracy: 1.0000
Epoch 3/30
600/600 [==============================] - 0s 727us/step - loss: 0.0036 - accuracy: 1.0000 - val_loss: 0.0026 - val_accuracy: 1.0000
Epoch 4/30
600/600 [==============================] - 0s 723us/step - loss: 0.0020 - accuracy: 1.0000 - val_loss: 0.0016 - val_accuracy: 1.0000
Epoch 5/30
600/600 [==============================] - 0s 723us/step - loss: 0.0014 - accuracy: 1.0000 - val_loss: 0.0011 - val_accuracy: 1.0000
Epoch 6/30
600/600 [==============================] - 0s 713us/step - loss: 9.7200e-04 - accuracy: 1.0000 - val_loss: 8.3221e-04 - val_accuracy: 1.0000
Epoch 7/30
600/600 [==============================] - 0s 697us/step - loss: 7.3653e-04 - accuracy: 1.0000 - val_loss: 6.4083e-04 - val_accuracy: 1.0000
Epoch 8/30
600/600 [==============================] - 0s 688us/step - loss: 5.7907e-04 - accuracy: 1.0000 - val_loss: 5.1182e-04 - val_accuracy: 1.0000
Epoch 9/30
600/600 [==============================] - 0s 712us/step - loss: 4.6838e-04 - accuracy: 1.0000 - val_loss: 4.1928e-04 - val_accuracy: 1.0000
Epoch 10/30
600/600 [==============================] - 0s 698us/step - loss: 3.8692e-04 - accuracy: 1.0000 - val_loss: 3.4947e-04 - val_accuracy: 1.0000
Epoch 11/30
600/600 [==============================] - 0s 723us/step - loss: 3.2525e-04 - accuracy: 1.0000 - val_loss: 2.9533e-04 - val_accuracy: 1.0000
Epoch 12/30
600/600 [==============================] - 0s 735us/step - loss: 2.7692e-04 - accuracy: 1.0000 - val_loss: 2.5270e-04 - val_accuracy: 1.0000
Epoch 13/30
600/600 [==============================] - 0s 710us/step - loss: 2.3846e-04 - accuracy: 1.0000 - val_loss: 2.1917e-04 - val_accuracy: 1.0000
Epoch 14/30
600/600 [==============================] - 0s 773us/step - loss: 2.0745e-04 - accuracy: 1.0000 - val_loss: 1.9093e-04 - val_accuracy: 1.0000
Epoch 15/30
600/600 [==============================] - 0s 718us/step - loss: 1.8180e-04 - accuracy: 1.0000 - val_loss: 1.6780e-04 - val_accuracy: 1.0000
Epoch 16/30
600/600 [==============================] - 0s 730us/step - loss: 1.6039e-04 - accuracy: 1.0000 - val_loss: 1.4876e-04 - val_accuracy: 1.0000
Epoch 17/30
600/600 [==============================] - 0s 698us/step - loss: 1.4249e-04 - accuracy: 1.0000 - val_loss: 1.3220e-04 - val_accuracy: 1.0000
Epoch 18/30
600/600 [==============================] - 0s 807us/step - loss: 1.2717e-04 - accuracy: 1.0000 - val_loss: 1.1842e-04 - val_accuracy: 1.0000
Epoch 19/30
600/600 [==============================] - 0s 722us/step - loss: 1.1404e-04 - accuracy: 1.0000 - val_loss: 1.0641e-04 - val_accuracy: 1.0000
Epoch 20/30
600/600 [==============================] - 1s 860us/step - loss: 1.0269e-04 - accuracy: 1.0000 - val_loss: 9.5853e-05 - val_accuracy: 1.0000
Epoch 21/30
600/600 [==============================] - 0s 768us/step - loss: 9.2805e-05 - accuracy: 1.0000 - val_loss: 8.6761e-05 - val_accuracy: 1.0000
Epoch 22/30
600/600 [==============================] - 0s 753us/step - loss: 8.4169e-05 - accuracy: 1.0000 - val_loss: 7.8690e-05 - val_accuracy: 1.0000
Epoch 23/30
600/600 [==============================] - 0s 727us/step - loss: 7.6554e-05 - accuracy: 1.0000 - val_loss: 7.1713e-05 - val_accuracy: 1.0000
Epoch 24/30
600/600 [==============================] - 0s 720us/step - loss: 6.9799e-05 - accuracy: 1.0000 - val_loss: 6.5581e-05 - val_accuracy: 1.0000
Epoch 25/30
600/600 [==============================] - 0s 715us/step - loss: 6.3808e-05 - accuracy: 1.0000 - val_loss: 5.9929e-05 - val_accuracy: 1.0000
Epoch 26/30
600/600 [==============================] - 0s 695us/step - loss: 5.8448e-05 - accuracy: 1.0000 - val_loss: 5.4957e-05 - val_accuracy: 1.0000
Epoch 27/30
600/600 [==============================] - 0s 730us/step - loss: 5.3656e-05 - accuracy: 1.0000 - val_loss: 5.0587e-05 - val_accuracy: 1.0000
Epoch 28/30
600/600 [==============================] - 0s 760us/step - loss: 4.9353e-05 - accuracy: 1.0000 - val_loss: 4.6493e-05 - val_accuracy: 1.0000
Epoch 29/30
600/600 [==============================] - 0s 750us/step - loss: 4.5461e-05 - accuracy: 1.0000 - val_loss: 4.2852e-05 - val_accuracy: 1.0000
Epoch 30/30
600/600 [==============================] - 0s 753us/step - loss: 4.1936e-05 - accuracy: 1.0000 - val_loss: 3.9584e-05 - val_accuracy: 1.0000
250/250 [==============================] - 0s 56us/step
Test results - Loss: 4.163062170846388e-05 - Accuracy: 100.0%</span></span></span></span>

如您所见，方形铰链也有效。比较两个决策边界 -

决策边界铰链

决策边界平方铰链

…平方铰链的决策边界似乎更接近或更紧密。也许是由于亏损形势的平稳性？然而，这不能肯定地说。

五、总结

在这篇博文中，我们了解了如何通过 hinge loss 和 squared hinge loss cost 函数使用 Keras 创建机器学习模型。我们从数学角度直观地引入了铰链损失和平方铰链，然后迅速进入实际实现。结果表明，铰链损失和平方铰链损失可以成功地用于非线性分类场景，但它们对数据集的可分离性相对敏感（是线性还是非线性并不重要）。