写在前面

这个专栏是记录我刷代码随想录过程中的随想和总结。每一小节都是根据自己的理解撰写的，文章比较短，主要是为了记录和督促自己。刷完一章后，我会再单独整理一篇文章来总结和分享。

本节对应代码随想录中：代码随想录-二分查找

原理

二分法（Binary Search）是一种在有序数组中查找特定元素的算法。它的原理是，将数组分成两半，然后判断目标元素在哪一半中，然后再继续将这一半分成两半，直到找到目标元素或者确定目标元素不存在为止。

前提条件：二分法适用于有序数组或有序列表中的查找操作，且元素必须支持比较操作。

一旦有重复元素的时候，二分法返回的下标可能不唯一

算法步骤如下：

1.将数组按照中间元素分成两部分。

2.如果中间元素等于目标元素，直接返回中间元素的下标。

3.如果中间元素大于目标元素，说明目标元素在左半部分，将右边界移动到中间元素的左边。

4.如果中间元素小于目标元素，说明目标元素在右半部分，将左边界移动到中间元素的右边。

5.重复以上步骤，直到找到目标元素或者确定目标元素不存在。

习题

题目1

704. 二分查找
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9     
输出: 4       
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2     
输出: -1        
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

思路和代码

这道题目说了元素是有序的，而且无重复元素，那么在查找的时候就可以使用二分法进行查找

写二分法会遇到三种情况

初始 right = nums.size()-1 还是 nums.size()
是 right = middle-1 还是 right = middle
是 while(left <= right) 还是 while(left < right)

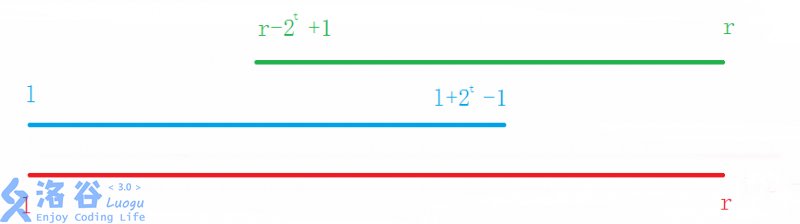
如下面这张图，left 等不等于 right，right 的取值也会不一样，可分为两种写法
在这里插入图片描述

如果初始写 right=nums.size()-1 即7个元素中 L=0，R=6，那么查找区间就是[0,6]，M 为3。
此时应该写 right = middle-1 。如上图 M=3时没有匹配成功，那么下次的区间应该是[0,2]，因为 M=3已经判断一次了
如上图如果 M=1时仍不是我们要找的元素，假如此时还是大于待查找元素，那么 R=0。此时 left=right=0是有意义的，也就是我们需要最后判定下 L=0时的1是不是待查找元素，因此 while 的条件为 while(left <= right)

这三种情况其实就是要互相对应，第二种类型在代码随想录中有解释

代码如下

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

注意取中间值时没有使用 middle = (left + right) / 2 而是 middle = left + ((right - left) / 2)

这样写能够避免 left + right 可能数值太大导致溢出的问题

例子：在闭区间[3,9]中 right-left=6，说明3到9需要走6步，再除2得3，说明从3到9走3步可以走到中间的位置

题目-2

35.搜索插入位置
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。

示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4

提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为无重复元素的升序排列数组
-104 <= target <= 104

代码如下

class Solution {
   public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0, right = n - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] > target) {
                right = right - 1;
            } else {
                left = left + 1;
            }
        }
        return left;
    }
};

观察上述代码可以发现这题和上题只是在上题 return -1 处改成了 return left

解释：上题的 return -1 和这里的 return left 都代表着所查找元素没有出现给定数组中的情况

至于目标值被插入的顺序为什么是 left。根据 if 的判断条件，left 左边的值一直保持小于 target，right 右边的值一直保持大于等于 target，而且 left 最终一定等于 right+1