文章目录
- 【 1、欧拉公式的频谱 】
- 【 2、模拟正交采样 】
- 【 3、数字正交采样 】
【 1、欧拉公式的频谱 】
-
对于余弦信号 c o s ( 2 π f 0 t ) = 1 2 e j 2 π f 0 t + 1 2 e − j 2 π f 0 t cos(2\pi f_0 t)=\frac{1}{2}e^{j2\pi f_0 t}+\frac{1}{2}e^{-j2\pi f_0 t} cos(2πf0t)=21ej2πf0t+21e−j2πf0t,对上式进行傅里叶变换得到
X c o s ( 2 π f 0 t ) ( f ) = 1 2 δ ( f − f 0 ) + 1 2 δ ( f + f 0 ) X_{cos(2\pi f_0t)}(f)=\frac{1}{2}\delta (f-f_0)+\frac{1}{2}\delta (f+f_0) Xcos(2πf0t)(f)=21δ(f−f0)+21δ(f+f0) -
相应的,对于正弦信号 s i n ( 2 π f 0 t ) = 1 2 j e − j 2 π f 0 t − j 1 2 e − j 2 π f 0 t sin(2\pi f_0 t)=\frac{1}{2}je^{-j2\pi f_0 t}-j\frac{1}{2}e^{-j2\pi f_0 t} sin(2πf0t)=21je−j2πf0t−j21e−j2πf0t,其傅里叶变换为
X ( f ) s i n ( 2 π f 0 t ) ( f ) = 1 2 j δ ( f + f 0 ) − 1 2 j δ ( f − f 0 ) X(f)_{sin(2\pi f_0t)}(f)=\frac{1}{2}j\delta (f+f_0)-\frac{1}{2}j\delta (f-f_0) X(f)sin(2πf0t)(f)=21jδ(f+f0)−21jδ(f−f0) -
反应在频谱上,为
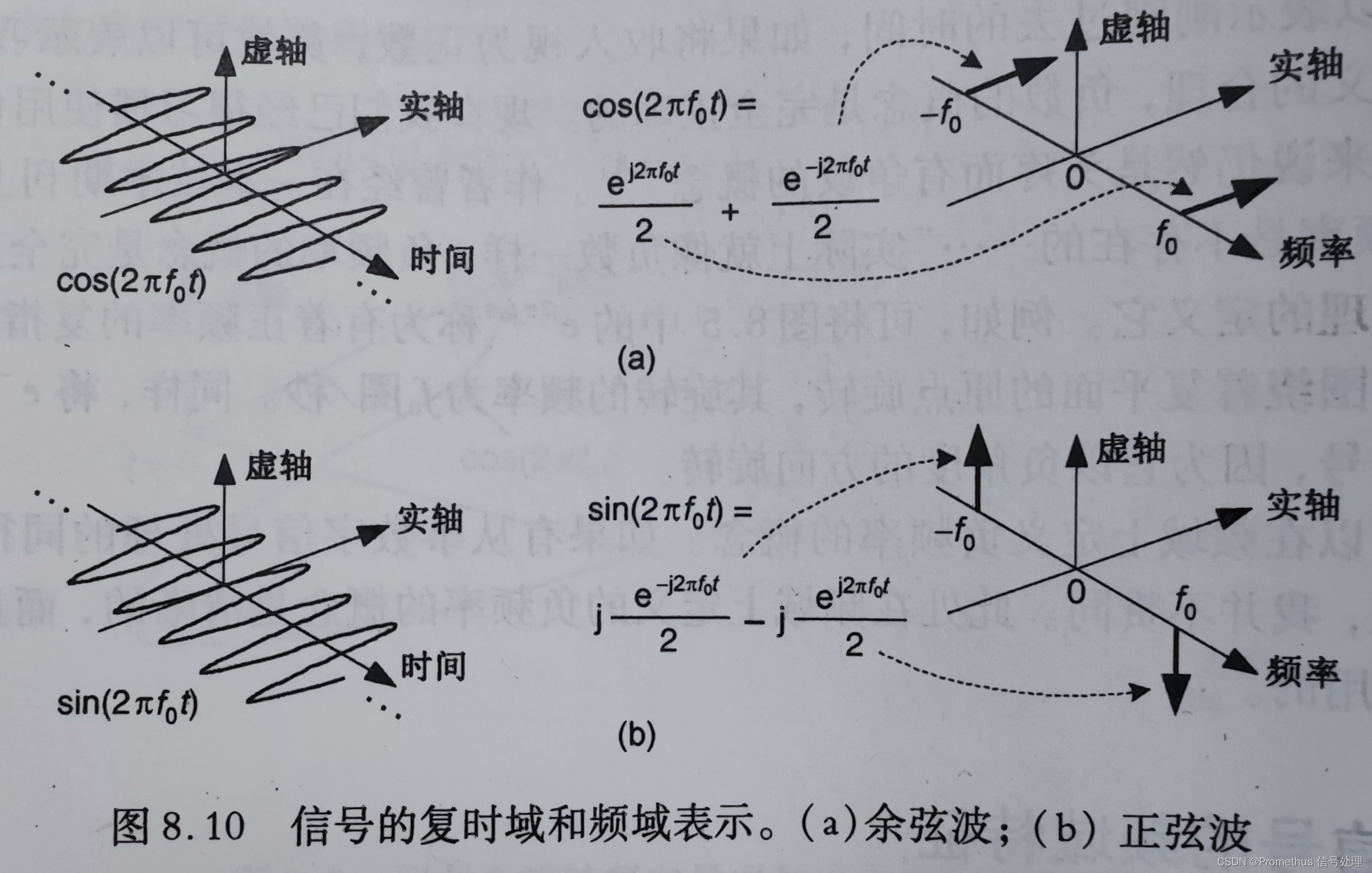
-
下面将正弦信号 s i n ( 2 π f 0 t ) sin(2\pi f_0 t) sin(2πf0t) 乘以 j (原信号乘以j相当于其频谱在复平面上逆时针旋转90°),再与余弦信号 c o s ( 2 π f 0 t ) cos(2\pi f_0 t) cos(2πf0t) 相加,得到: e j 2 π f 0 t = c o s ( 2 π f 0 t ) + j s i n ( 2 π f 0 t ) e^{j2\pi f_0 t}=cos(2\pi f_0 t)+jsin(2\pi f_0 t) ej2πf0t=cos(2πf0t)+jsin(2πf0t),其频谱可表示为:
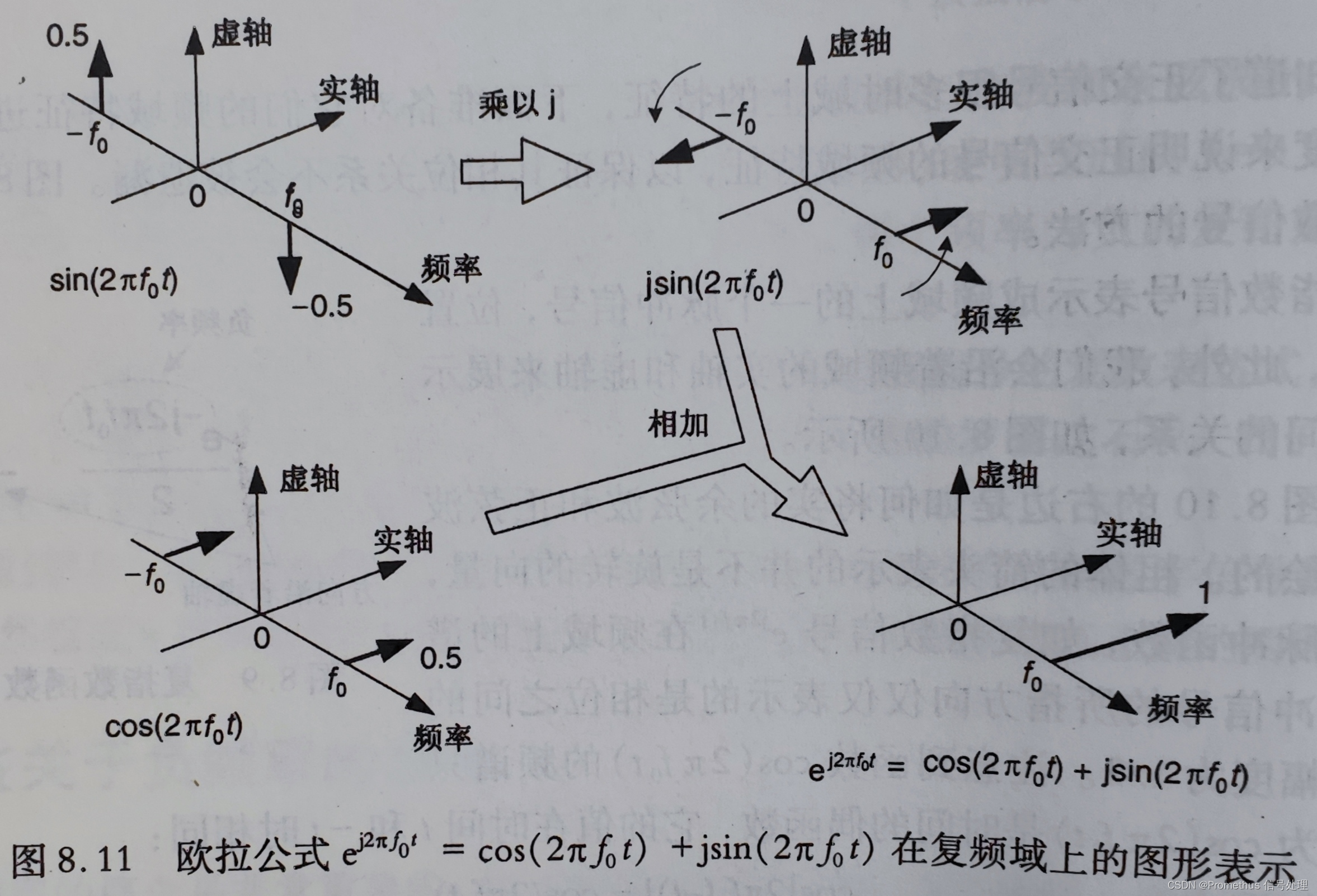
-
将一个时域信号乘以复指数信号 e j 2 π f 0 t e^{j2\pi f_0 t} ej2πf0t,可以使频谱向上搬移 f 0 f_0 f0 Hz,该过程被称为 正交混频(也称为复混频);类似的,将一个时域信号乘以复指数信号 e j 2 π f 0 t e^{j2\pi f_0 t} ej2πf0t,可以将其频谱向下搬移 f 0 f_0 f0 Hz。即傅里叶变换的频移公式: e ± j 2 π f 0 t f ( t ) = X ( f ∓ f 0 ) e^{±j2\pi f_0t }f(t)=X(f∓f_0) e±j2πf0tf(t)=X(f∓f0)。
【 2、模拟正交采样 】
- 如下图 a 所示,为正交采样的过程,输入带通信号
x
b
p
(
t
)
x_{bp}(t)
xbp(t) 分别与
c
o
s
(
2
π
f
0
t
)
cos(2\pi f_0 t)
cos(2πf0t)、
−
s
i
n
(
2
π
f
0
t
)
-sin(2\pi f_0 t)
−sin(2πf0t) 相乘,得到
x
i
(
t
)
x_i(t)
xi(t)、
x
q
(
t
)
x_q(t)
xq(t);再经 LPF低通滤波器,得到低通分量
i
(
t
)
、
q
(
t
)
i(t)、q(t)
i(t)、q(t);最后经过模数转换器,得到数字量
i
(
n
)
、
q
(
n
)
i(n)、q(n)
i(n)、q(n),并合成为解析信号
x
c
(
n
)
=
i
(
n
)
+
q
(
n
)
x_c(n)=i(n)+q(n)
xc(n)=i(n)+q(n),后面几图分别为各分量的频谱。
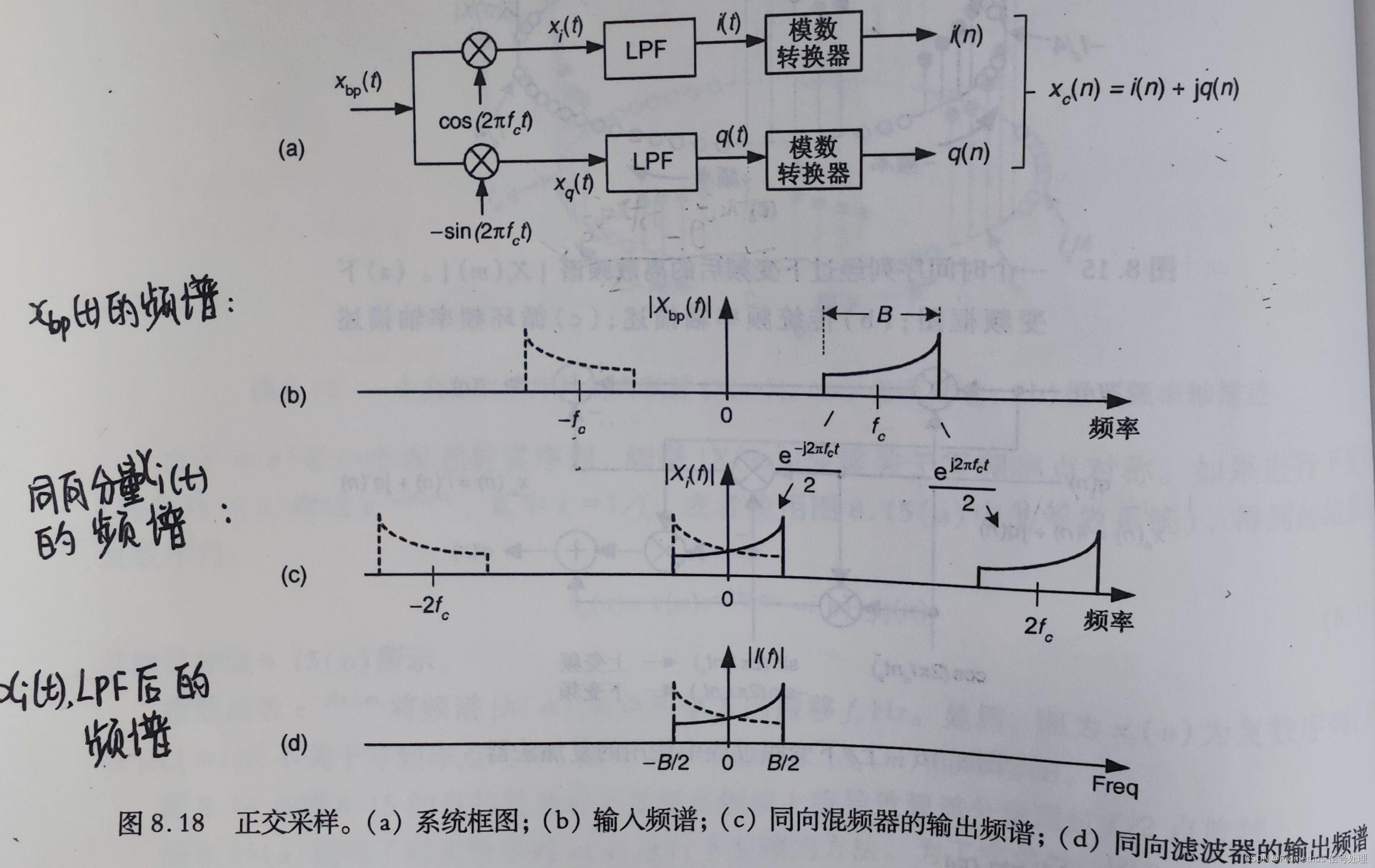
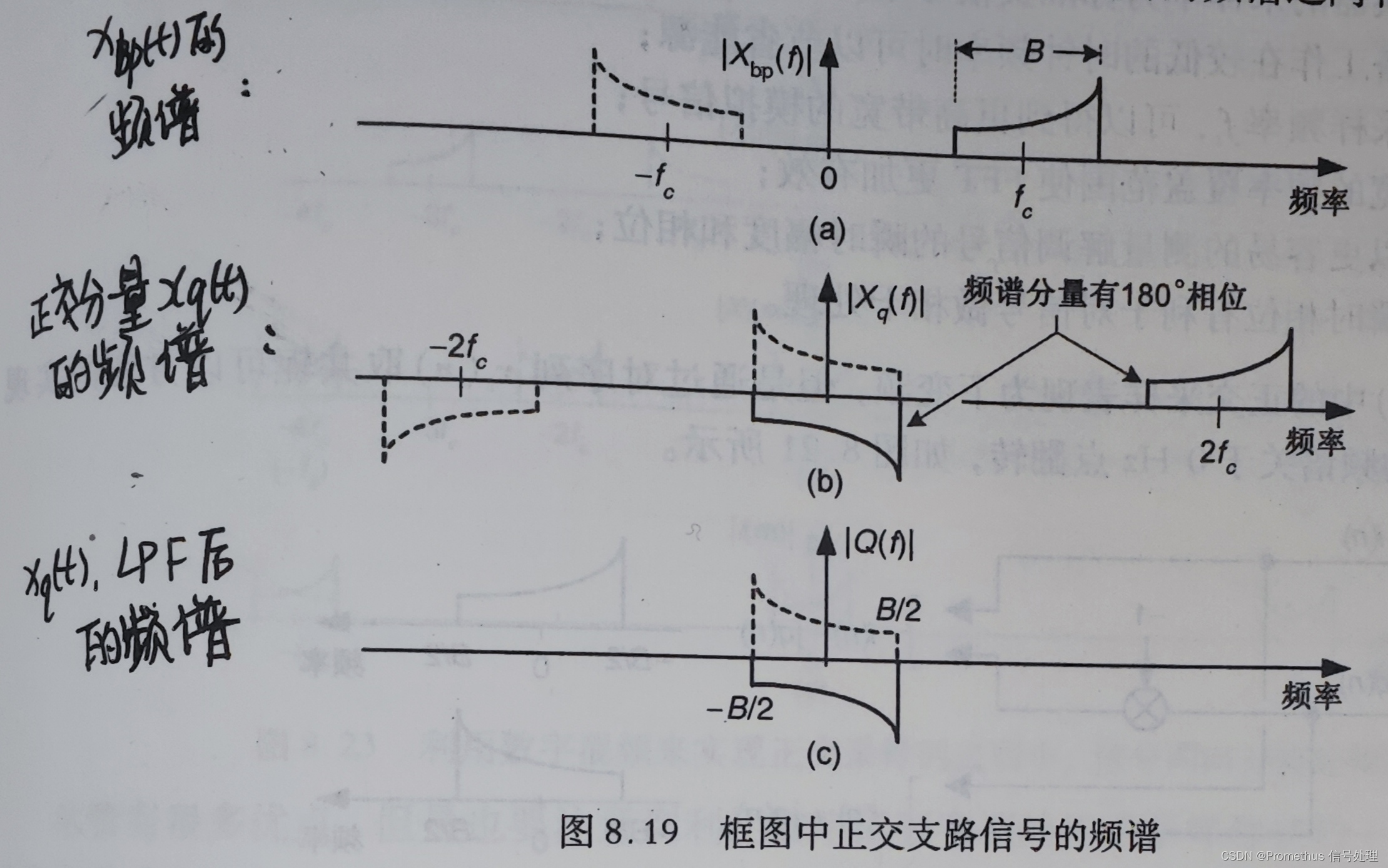

【 3、数字正交采样 】
- 低通滤波法

-
插值法

-
多相滤波法