【NLP经典论文阅读】Efficient Estimation of Word Representations in Vector Space(附代码)
1. 论文简介
Efficient Estimation of Word Representations in Vector Space(以下简称Word2vec)是一篇由Google的Tomas Mikolov等人于2013年发表的论文,该论文提出了一种基于神经网络的词向量训练方法,能够高效地学习到单词在向量空间中的分布式表示。
出处:https://arxiv.org/abs/1301.3781
作者:Tomas Mikolov, Kai Chen, Greg Corrado, Jeffrey Dean
单位:Google
发表年份:2013年
论文大意:
论文提出了两种新的模型架构,用于从非常大的数据集中计算单词的连续向量表示。这些表示的质量通过单词相似性任务进行衡量,并将结果与基于不同类型的神经网络的先前表现最佳的技术进行比较。我们观察到准确率有大幅提升,而计算成本则更低,即从一个16亿个单词的数据集中学习高质量单词向量只需不到一天的时间。此外,我们展示了这些向量在测量句法和语义单词相似性的测试集上提供了最先进的性能。
2. 论文详解
Word2vec的主要思想是通过预测上下文或目标单词的方法学习单词的向量表示。具体来说,Word2vec通过一个简单的神经网络来学习单词的向量表示,该神经网络包括一个输入层、一个隐藏层和一个输出层。输入层接收到一个单词,将其转换为一个向量表示,然后将该向量传递到隐藏层中。隐藏层对输入向量进行一些变换,然后将结果传递到输出层。输出层则根据上下文或目标单词的不同,采用不同的损失函数来计算损失,然后通过反向传播算法来更新模型参数。
Word2vec有两种模型,分别是CBOW模型和Skip-gram模型。CBOW模型根据上下文单词来预测中心单词,而Skip-gram模型则根据中心单词来预测上下文单词。在训练时,Word2vec通过梯度下降算法来最小化损失函数,并将单词的向量表示作为最终的输出。

相比传统的词向量方法,Word2vec的优点在于它能够高效地处理大量的语料库,从而学习到更加准确的单词向量表示。此外,Word2vec的向量表示能够自动捕捉到单词之间的语义和语法关系,因此在自然语言处理任务中表现出了良好的性能。
除了论文之外,Word2vec的相关代码也已经在GitHub上开源,可以在https://github.com/tmikolov/word2vec上找到。在该项目中,提供了C++和Python两种版本的实现代码,包括CBOW和Skip-gram两种模型以及负采样和层次softmax两种训练方法。
2.1 Skip-gram
在Skip-gram模型中,我们的目标是通过中心单词来预测上下文单词。对于给定的一对(中心单词,上下文单词),我们希望最大化它们的共现概率。
假设我们有一个长度为
T
T
T的文本序列
w
1
,
w
2
,
.
.
.
,
w
T
w_1,w_2,...,w_T
w1,w2,...,wT,我们的目标是最大化以下条件概率的对数似然函数:
L
(
θ
)
=
1
T
∑
t
=
1
T
∑
−
c
≤
j
≤
c
,
j
≠
0
log
p
(
w
t
+
j
∣
w
t
;
θ
)
L(\theta)=\frac{1}{T}\sum_{t=1}^T\sum_{-c\le j\le c,j\ne 0}\log p(w_{t+j}|w_t;\theta)
L(θ)=T1t=1∑T−c≤j≤c,j=0∑logp(wt+j∣wt;θ)
其中,
c
c
c是上下文单词的窗口大小,
θ
\theta
θ是模型的参数。
我们使用Softmax函数来估计每个上下文单词的概率:
p ( w t + j ∣ w t ; θ ) = exp ( v w t + j ′ ⋅ v w t ) ∑ i = 1 W exp ( v i ′ ⋅ v w t ) p(w_{t+j}|w_t;\theta)=\frac{\exp(v_{w_{t+j}}'\cdot v_{w_t})}{\sum_{i=1}^W\exp(v_i'\cdot v_{w_t})} p(wt+j∣wt;θ)=∑i=1Wexp(vi′⋅vwt)exp(vwt+j′⋅vwt)
其中, v w v_w vw和 v w ′ v'_w vw′分别表示单词 w w w在输入和输出层中的向量表示, W W W是词汇表大小。
2.2 CBOW模型
CBOW模型与Skip-gram模型类似,但是反过来。在CBOW模型中,我们的目标是通过上下文单词来预测中心单词。具体来说,我们希望最大化中心单词和其上下下文单词的共现概率,公式如下:
L
(
θ
)
=
1
T
∑
t
=
1
T
log
p
(
w
t
∣
w
t
−
c
,
…
,
w
t
−
1
,
w
t
+
1
,
…
,
w
t
+
c
;
θ
)
L(\theta)=\frac{1}{T}\sum_{t=1}^T\log p(w_t|w_{t-c},\ldots,w_{t-1},w_{t+1},\ldots,w_{t+c};\theta)
L(θ)=T1t=1∑Tlogp(wt∣wt−c,…,wt−1,wt+1,…,wt+c;θ)
其中,
c
c
c是上下文单词的窗口大小,
θ
\theta
θ是模型的参数。
我们使用Softmax函数来估计中心单词的概率:
p
(
w
t
∣
w
t
−
c
,
…
,
w
t
−
1
,
w
t
+
1
,
…
,
w
t
+
c
;
θ
)
=
exp
(
∑
j
=
−
c
,
j
≠
0
c
v
w
t
+
j
)
∑
i
=
1
W
exp
(
∑
j
=
−
c
,
j
≠
0
c
v
w
t
+
j
)
p(w_t|w_{t-c},\ldots,w_{t-1},w_{t+1},\ldots,w_{t+c};\theta)=\frac{\exp(\sum_{j=-c,j\ne 0}^cv_{w_{t+j}})}{\sum_{i=1}^W\exp(\sum_{j=-c,j\ne 0}^cv_{w_{t+j}})}
p(wt∣wt−c,…,wt−1,wt+1,…,wt+c;θ)=∑i=1Wexp(∑j=−c,j=0cvwt+j)exp(∑j=−c,j=0cvwt+j)
其中, v w v_w vw和 v w ′ v'_w vw′分别表示单词 w w w在输入和输出层中的向量表示, C C C是上下文单词的数量, W W W是词汇表大小。
2.3 模型优化
在训练Word2Vec模型时,我们需要最大化对数似然函数。由于词汇表很大,如果使用标准的梯度下降法来优化模型,计算量将非常大。为了解决这个问题,作者提出了两种方法:Hierarchical Softmax和Negative Sampling。
2.3 Hierarchical Softmax
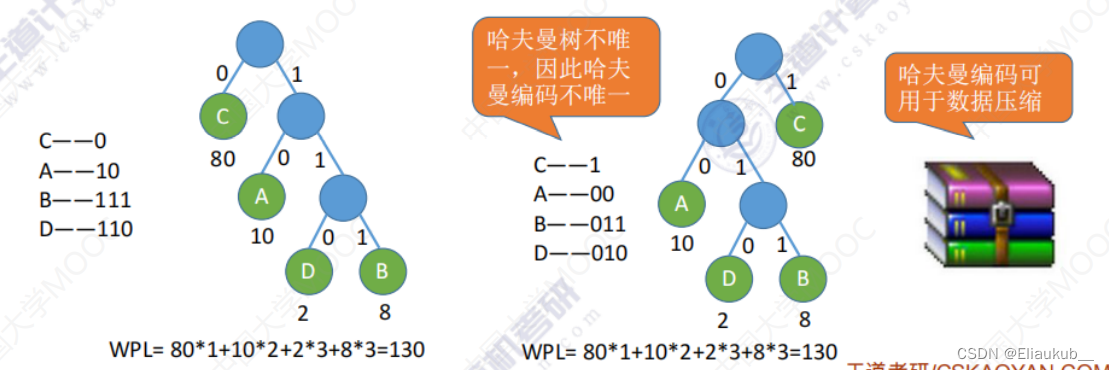
在Hierarchical Softmax中,我们将输出层的单词表示为一个二叉树,其中每个叶子节点都表示一个单词。每个非叶子节点都表示两个子节点的内积,每个叶子节点都表示该单词的条件概率。由于二叉树的形状,我们可以使用 log 2 W \log_2 W log2W个节点来表示词汇表大小为 W W W的模型,这将大大降低计算量。
在使用Hierarchical Softmax进行训练时,我们需要通过二叉树来计算每个上下文单词的概率,如下所示:
p
(
w
t
+
j
∣
w
t
)
=
exp
(
v
w
t
+
j
T
⋅
v
w
t
)
∑
i
=
1
W
exp
(
v
i
T
⋅
v
w
t
)
=
exp
(
score
(
w
t
+
j
,
w
t
)
)
∑
i
=
1
W
exp
(
score
(
w
i
,
w
t
)
)
p(w_{t+j}|w_t)=\frac{\exp(v_{w_{t+j}}^T\cdot v_{w_t})}{\sum_{i=1}^W\exp(v_i^T\cdot v_{w_t})}=\frac{\exp(\text{score}(w_{t+j},w_t))}{\sum_{i=1}^W\exp(\text{score}(w_i,w_t))}
p(wt+j∣wt)=∑i=1Wexp(viT⋅vwt)exp(vwt+jT⋅vwt)=∑i=1Wexp(score(wi,wt))exp(score(wt+j,wt))
其中, l ( w O ) l(w_O) l(wO)是单词 w O w_O wO在二叉树中的深度, n ( w O , j ) n(w_O,j) n(wO,j)表示在单词 w O w_O wO的路径上第 j j j个节点, σ ( x ) = 1 1 + exp ( − x ) \sigma(x)=\frac{1}{1+\exp(-x)} σ(x)=1+exp(−x)1是Sigmoid函数。
2.4 Negative Sampling
在Negative Sampling中,我们将每个训练样本拆分成多个二元组
(
w
I
,
w
O
)
(w_I,w_O)
(wI,wO),其中
w
I
w_I
wI是中心单词,
w
O
w_O
wO是上下文单词。
对于每个二元组,我们随机采样
K
K
K个噪声单词,用它们来计算负样本。具体地,我们将每个单词的概率提高到
3
/
4
3/4
3/4次方,并进行归一化,得到单词
w
w
w的采样概率:
P sample ( w ) = f ( w ) 3 / 4 ∑ i = 1 W f ( w i ) 3 / 4 P_{\text{sample}}(w)=\frac{f(w)^{3/4}}{\sum_{i=1}^{W}f(w_i)^{3/4}} Psample(w)=∑i=1Wf(wi)3/4f(w)3/4
其中, f ( w ) f(w) f(w)是单词 w w w在训练语料中出现的频次。
在使用Negative Sampling进行训练时,我们的目标是最小化负样本的概率和中心单词的概率的负对数似然:
− log σ ( v w O ′ ⋅ v w I ) − ∑ k = 1 K log σ ( − v w k ′ ⋅ v w I ) -\log\sigma(v'_{w_O}\cdot v_{w_I})-\sum_{k=1}^{K}\log\sigma(-v'_{w_k}\cdot v_{w_I}) −logσ(vwO′⋅vwI)−k=1∑Klogσ(−vwk′⋅vwI)
其中, w k w_k wk是噪声单词, σ ( x ) = 1 1 + exp ( − x ) \sigma(x)=\frac{1}{1+\exp(-x)} σ(x)=1+exp(−x)1是Sigmoid函数。
使用Negative Sampling的优点在于计算速度较快,但是它有可能丢失一些信息,因为它只考虑了一部分的负样本。
3. 代码实现
下面,我们通过一个简单的案例来演示如何使用Word2vec训练词向量。首先,我们需要下载并解压缩一个语料库,例如维基百科的语料库。然后,我们可以使用Python中的gensim库来训练词向量。具体代码如下:
import gensim
from gensim.models import Word2Vec
# 加载语料库
sentences = gensim.models.word2vec.Text8Corpus('path/to/corpus')
# 训练模型
model = Word2Vec(sentences, size=100, window=5, min_count=5, workers=4)
# 保存模型
model.save('path/to/model')
# 加载模型
model = Word2Vec.load('path/to/model')
# 获取单词向量
vector = model['word']
在上面的代码中,我们首先使用Text8Corpus类加载语料库,然后使用Word2Vec类来训练模型。其中,size参数指定了向量的维度,window参数指定了上下文单词的窗口大小,min_count参数指定了单词出现的最小次数,workers参数指定了使用的线程数。训练完成后,我们可以使用save和load方法来保存和加载模型,使用model[‘word’]来获取单词的向量表示。
通过Word2vec训练出的词向量可以用于许多自然语言处理任务,例如词义相似度计算、命名实体识别和情感分析等。例如,在情感分析任务中,我们可以通过将一句话中的单词向量取平均来获取该句话的向量表示,然后使用分类器来对其进行情感分类。该方法在许多情感分析任务中表现出了良好的性能。