1 概述

本文是ICCV2019的一篇论文，核心是提出了一种简单的end-to-end的two-stage的检测图像中线段的方法。同时，文章也提出了一种新的评价线段检测效果的指标，这个指标可以惩罚同一个位置有交叠的线段预测，也可以惩罚连接错误的线段。

概括地说，就是一个two-stage的方法L-CNN和一个新的线段评价指标Structural AP(sAP)。

L-CNN可以被分为四个部分：
（1）backbone
用于抽取图像的特征。
（2）juction proposal module
第一阶段中提出节点的proposal的模块，如果这部分有节点没有召回，那后面线段就不可能预测出来了。这是直接影响召回率recall的阶段。
（3）line sample module
负责线段的采样，这是为了给第二阶段提供正负样本进行训练。如果是预测，则认为所有第一节点proposal得到的节点两两相连都作为采样得到的线段。
（4）line verificatoin module
这是第二阶段判断（3）采样得到的线段是否是线段的判别器。这是直接影响精确率precision的阶段。

L-CNN可以吃RGB的输入，然后直接输出线段向量，不需要任何的启发式算法。

在这篇文章之前的论文所使用的评价指标都是像素级别的，认为线段是由独立的像素点集合所构成。本文提出了一种新的线段评价指标sAP，sAP将线段视为一个整体，然后再去计算线段级别的precision和recall。

2 L-CNN

2.1 整体架构

模型的整体架构如下图2-1所示，首先输入RGB图片，图片会经过backbone抽取特征得到一张feature map；feature map经过一些卷积会得到junction heatmap，这个heatmap是模型判断该位置是节点的候选概率图；根据节点的候选概率图，line sampler会sample线段，作为可能存在的线段输入下个模块；最后通过line verification模块来判断sample出来的线段是不是真的线段，每条sample出来的线段会根基feature map得到该线段的特征，再进入判别器进行判别。

最终的输出是节点的位置，以及表示节点之间是否相连的矩阵。

整个网络可以通过SGD进行end-to-end的训练。

图2-1 L-CNN网络结构图

2.2 backbone

backbone需要抽取到图片中线段的特征，本文选取的是stacked hourglass network，这是在关键点检测中经常使用的backbone，在这里用来抽取节点和线段的特征非常合适。

stacked hourglass network的Loss即是其他所有模块的Loss之和，也就是其他的模块损失对backbone都会造成影响。

2.3 juction proposal module

在进行节点的预测时，会将$H\times W$的图片切分为尺寸为$H_b\times W_b$的多个bins，也可以理解为grids。每个bin预测是否有节点在这个bin之内，如果这个bin之内有节点，还会预测节点在这个bin当中的相对位置。总的来说，juction proposal module会输出一个节点的概率图$J$和节点的位置偏移图$O$。

概率图$J$的GT(ground truth)用数据公式可以表达为

$$J(b)=\{\begin{array}{ll}1& \exists i\in V:{\mathbf{p}}_i\in b,\\ 0& otherwise\end{array}\text{\hspace{1em}(2-1)}$$

其中，$J$表示节点概率图；$b$表示某个bin；$V$表示所有真是存在的节点；${\mathbf{p}}_i$表示第$i$个节点的坐标；

$$O(b)=\{\begin{array}{ll}(\mathbf{b}-{\mathbf{p}}_i)/W_b& \exists i\in V:p_i\in b,\\ 0& otherwise\end{array}\text{\hspace{1em}(2-2)}$$

其中，$O$表示相对位置偏移图；$\mathbf{b}$表示$b$的中心点坐标；其余同式$(2-1)$。

按这里的表示，$\mathbf{b}$是可能超出bin的。个人式$(2-2)$中的$W_b$应该换成bin的宽度。

从feature map变成$J$和$O$会分别经过$1\times 1$的卷积。

作者将预测$J$视为一个分类问题，即每个bin是否有节点的二分类，使用the average binary cross entropy loss。

将预测$O$视为回归问题，通过sigmoid函数，并减去0.5的偏置，将$O(b)$限制在$[-0.5,0.5)$的值域内，loss使用的是L2 loss。注意这里在计算loss时，只对有真实节点落在其中的bin进行计算，并在最后取平均。

预测为节点的bin一般不会单独出现，而是像聚类一样成群出现的，只不过真正节点所在的bin分数最高，周围的bin分数低一些。为了去除这些正确的bin附近的bin，作者采用了nms的方法，将bin八邻域的节点进行抑制。这里的nms只需要通过max pool来实现就可以了。

$$J^{\prime }(b)=\{\begin{array}{ll}J(b)& J(b)=ma{x}_{b^{\prime }\in N(b)}J(b^{\prime })\\ 0& otherwise\end{array}$$

其中，$N(b)$就是$b$的八邻域。

最后会根据分数从$J^{\prime }$中选择topK个节点作为最终预测的节点 { p ^ i } i = 1 K \{\hat{\bold{p}}_i\}_{i=1}^K {p^​i​}i=1K​。

2.4 line sample module

有了 { p ^ i } i = 1 K \{\hat{\bold{p}}_i\}_{i=1}^K {p^​i​}i=1K​，其实我们可以将K个节点之间两两相连的线段作为proposal放入line verificatoin module中进行预测，共有$C_K^2$条线段。但是这样大部分的线段都是负样本，正样本在其中的比例太少了，正负样本极度不平衡。这对于模型的训练影响很大。不过预测阶段，直接取$C_K^2$条线段进行line verificatoin即可。

为了解决proposal正负样本不平衡的问题，作者突出了静态采样和动态采样两种方案。

图2-2 静态和动态采样示意图

图2-2是静态和动态采样的示意图，红色的节点是GT节点，红色的线段是GT线段，绿色的节点是预测的节点，蓝色的线段是proposal的线段。如果没有静态和动态采样，也就是预测时候的采样方式，就是图2-2(d)所示的方式。

（1）静态采样
静态采样，顾名思义，就是不随着模型预测结果发生变化的，因为它是根据GT来进行采样的。这就避免了模型训练初期，一阶段模型不够好，预测的节点大多是错误节点，导致二阶段拿不到正样本的问题。这个RNN当中的teacher forcing有点相似。

静态采样的正样本$S^{+}$，就是真实的线段，如图2-2(b)所示。

静态采样的负样本$S^{-}$，是一些难负样本，它在除了$S^{+}$之外的，真实节点之间两两相连的线段之间进行选择，选择时，会将所有的真实线段映射到$64\times 64$的低分辨率二值图中，有真实线段经过的网格点置为1，其余为0，统计待选择的线段在低分辨率二值图中经过的网格点的分数和的平均。最终取分数最高的top 2000条线段作为$S^{-}$，如图2-2©所示。

（2）动态采样
动态采样是根据模型预测的节点进行采样的。图2-2(d)中的$D^{\ast }$即是所有预测节点之间两两相连的结果。

令$m_i:=arg{\min }_j||{\hat{\mathbf{p}}}_i-{\mathbf{p}}_j|{|}_2$，表示于预测节点${\hat{\mathbf{p}}}_i$最接近的真实节点${\mathbf{p}}_{m_i}$。如果${\mathbf{p}}_{m_i}$和${\hat{\mathbf{p}}}_i$之间的L2距离小于$\eta$，则认为${\hat{\mathbf{p}}}_i$匹配上了一个真实节点，成为matched。

在所有matched的节点中，如果${\hat{\mathbf{p}}}_{i1}$和${\hat{\mathbf{p}}}_{i2}$对应的${\mathbf{p}}_{m_{i1}}$和${\mathbf{p}}_{m_{i2}}$不是同一个点，且${\mathbf{p}}_{m_{i1}}$和${\mathbf{p}}_{m_{i2}}$之间的连线属于$S^{+}$，那就认为${\hat{\mathbf{p}}}_{i1}$和${\hat{\mathbf{p}}}_{i2}$的连线属于$D^{+}$，如图2-2(e)所示。

在所有matched的节点中，如果${\hat{\mathbf{p}}}_{i1}$和${\hat{\mathbf{p}}}_{i2}$对应的${\mathbf{p}}_{m_{i1}}$和${\mathbf{p}}_{m_{i2}}$不是同一个点，且${\mathbf{p}}_{m_{i1}}$和${\mathbf{p}}_{m_{i2}}$之间的连线属于$S^{-}$，那就认为${\hat{\mathbf{p}}}_{i1}$和${\hat{\mathbf{p}}}_{i2}$的连线属于$D^{-}$，如图2-2(e)所示。

最终从$D^{+}$中取$N_{D^{+}}$作为动态采样的正样本，从$D^{-}$中取$N_{D^{-}}$作为动态采样的负样本，从$D^{\ast }$中取$N_{D^{\ast }}$条与$N_{D^{+}}$和$N_{D^{-}}$不重复的线段，若线段存在于$D^{+}$则为正样本，否则是负样本。

总的来说，静态采样有助于模型的前期训练，动态采样可以让模型对预测得到的线段有更正确的判别。

2.5 line verificatoin module

令2.4中采样得到的线段proposal为 { L j } j = 1 M = { ( p j 1 , p j 2 ) } j = 1 M \{L_j\}_{j=1}^M = \{ (\bold{p}_j ^ 1, \bold{p}_j ^ 2) \}_{j=1}^M {Lj​}j=1M​={(pj1​,pj2​)}j=1M​，每条线段$L_j=({\mathbf{p}}_j^1,{\mathbf{p}}_j^2)$对应于backbone中feature map的一些特征，但是每条线段的长度不同，特征向量的长度也就不同了。这与Faster-RCNN中遇到proposal的图片尺寸不一致的问题一样，这里作者也效仿了RoI Pooling，设计了一种LoI Pooling。

LoI Pooling的做法是对$L_j$线段进行空间上均匀分布的采样，每条线段都采$N_p$个点，每个点的特征是根据点落在feature map上的位置进行双线性插值得到的。如此一来，经过LoI Pooling的每条线段的特征维度都保持了一致。最终将得到的特征concat起来，输入全连接网络进行判别是否是线段。

3 评价指标

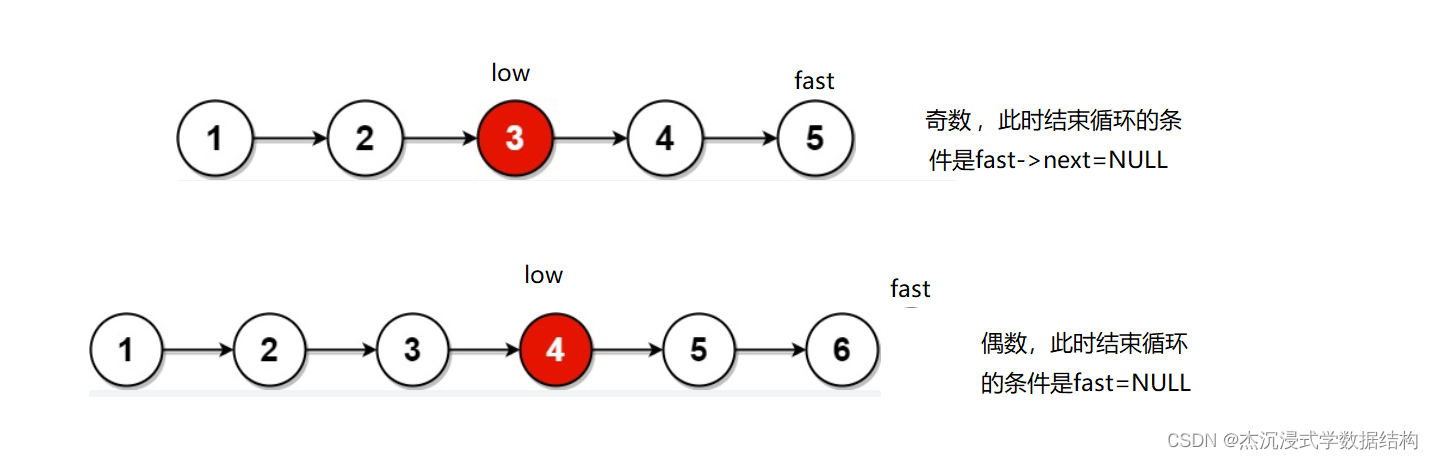
在本文之前评价线段预测结果的方法都是$A{P}^H$。$A{P}^H$是将GT线段和预测线段都转换为像素，GT对应的像素在预测结果中也被预测为线段，则该像素点就是TP(true positive)了，然后比较像素的precision和recall。这种方式对于下图3-1所示的两种情况不能处理，一种是预测线段交叠的情况，另一种是节点连接错误的情况。因为这些情况下，映射到像素级别的图上的结果是一致的。

主要问题在于，这种方式并没有将线段视作一个整体。

图3-1 基于heatmap的方式不适用的示例

为了克服上述的缺点，本文提出了structural average precision (sAP)。这个方法是受目标检测的指标启示得出的。sAP中的TP是线段，只有当预测的线段满足式$(3-1)$的条件时，才认为是TP。

$$\underset{(u,v)\in E}{\min }||{\mathbf{p}}_j^1-{\mathbf{p}}_u|{|}_2^2+||{\mathbf{p}}_j^2-{\mathbf{p}}_v|{|}_2^2\le \theta \text{\hspace{1em}(3-1)}$$

通俗地来说就是，预测线段的两个节点距离预期匹配的真实线段的两个节点的距离都小于$\theta$，则认为是TP。

其中，$\theta$的取值表示了严格度，本文中取$\theta =5$，$\theta =10$，$\theta =15$分别进行计算，对应的表示为$sA{P}^5$，$sA{P}^{10}$，$sA{P}^{15}$。

需要注意的是，一条GT被认为TP过一次，就不能再被认为是TP了，这避免了一条线段被预测为多条线段的问题。

参考资料

[1] End-to-End Wireframe Parsing
[2] https://github.com/zhou13/lcnn