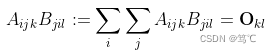传送门:牛客
题目描述:
A tree structure with some colors associated with its vertices and a sequence of commands on it are
given. A command is either an update operation or a query on the tree. Each of the update operations
changes the color of a specified vertex, without changing the tree structure. Each of the queries asks
the number of edges in the minimum connected subgraph of the tree that contains all the vertices of
the specified color.
Your task is to find answers of each of the queries, assuming that the commands are performed in
the given order.
输入:
5
1 2
2 3
3 4
2 5
1 2 1 2 3
11
Q 1
Q 2
Q 3
Q 4
U 5 1
Q 1
U 3 2
Q 1
Q 2
U 5 4
Q 1
输出:
2
2
0
-1
3
2
2
0
一道比较难想的树形结构题吧.
对于这道题我们解决的是对于新加入的这个点所增加的贡献是多少,我们可以画个图来帮助理解一下.对于一个改变的一个k,与原来的两个点<u,v>,我们有以下几种关系.

假设此时的三个点(u,v,g)的颜色是相同的,那么对于此时新增的三个可能位置
k
1
,
k
2
,
k
3
k1,k2,k3
k1,k2,k3来说,假设新增的是k2,我们会发现新增的贡献就是
(
d
i
s
(
k
,
u
)
+
d
i
s
(
k
,
v
)
−
d
i
s
(
u
,
v
)
)
/
2
(dis(k,u)+dis(k,v)-dis(u,v))/2
(dis(k,u)+dis(k,v)−dis(u,v))/2或者
(
d
i
s
(
k
,
u
)
+
d
i
s
(
k
,
g
)
−
d
i
s
(
u
,
g
)
)
/
2
(dis(k,u)+dis(k,g)-dis(u,g))/2
(dis(k,u)+dis(k,g)−dis(u,g))/2
假设此时新增的是k3,我们会发现此时新增的贡献还是:
(
d
i
s
(
k
,
u
)
+
d
i
s
(
k
,
v
)
−
d
i
s
(
u
,
v
)
)
/
2
(dis(k,u)+dis(k,v)-dis(u,v))/2
(dis(k,u)+dis(k,v)−dis(u,v))/2
假设此时新增的是k,我们会发现新增的贡献是:
(
d
i
s
(
k
,
u
)
+
d
i
s
(
k
,
g
)
−
d
i
s
(
u
,
g
)
)
/
2
(dis(k,u)+dis(k,g)-dis(u,g))/2
(dis(k,u)+dis(k,g)−dis(u,g))/2或者(dis(k,v)+dis(k,g)-dis(v,g))/2
那么此时我们会发现存在这样的一个规律,就是对于新加的一个点k来说,此时我们需要找到之前颜色与之相同的所有点,然后找到一个dfs序里他最近的一个点u,然后再随便的找另一个点v,那么对于此时的新增的贡献来说就是
(
d
i
s
(
k
,
u
)
+
d
i
s
(
k
,
v
)
−
d
i
s
(
u
,
v
)
)
/
2
(dis(k,u)+dis(k,v)-dis(u,v))/2
(dis(k,u)+dis(k,v)−dis(u,v))/2
为了解题方便起见,我们可以规定v的dfs序刚好是离k第二近的一个点.对于找点可以使用二分进行解决
我们先求出所有点的dfs序,然后对于新加的点,我们直接对这个颜色加上相应的贡献.此时需要注意的一点是当我们的颜色只有一个点时,此时我们规定上述的u,v都是这个点.然后对于删除的点,我们删除他此时的贡献即可.假设一个颜色没有点了,此时我们将其的ans改为-1
因为我们需要进行删除与增加操作,以及排序操作,对于维护这些性质我们可以使用
s
e
t
set
set进行解决.
对于求解树上两点之间距离,我们可以使用树链剖分或者倍增来求LCA进行求解,此处就不再赘述了.
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {
ll x=0,w=1;char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
#define maxn 1000000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int n;
vector<int>edge[maxn];
int fa[maxn],Size[maxn],max_son[maxn],dep[maxn];
int dfsn[maxn],dfscnt=0,rev[maxn];
void dfs1(int u,int per_u) {
Size[u]=1;dfsn[u]=++dfscnt;rev[dfscnt]=u;
for(int i=0;i<edge[u].size();i++) {
int v=edge[u][i];
if(v==per_u) continue;
dep[v]=dep[u]+1;
dfs1(v,u);
Size[u]+=Size[v];fa[v]=u;
if(Size[v]>Size[max_son[u]]) {
max_son[u]=v;
}
}
}
int top[maxn];
void dfs2(int u,int t) {
top[u]=t;
if(!max_son[u]) return ;
dfs2(max_son[u],t);
for(int i=0;i<edge[u].size();i++) {
int v=edge[u][i];
if(v==fa[u]||v==max_son[u]) continue;
dfs2(v,v);
}
}
int LCA(int u,int v) {
while(top[u]!=top[v]) {
if(dep[top[u]]<dep[top[v]]) swap(u,v);
u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
return u;
}
/*====================================================================*/
set<int>c[maxn];int ans_c[maxn];int a[maxn];
int get_dist(int u,int v) {
return dep[rev[u]]+dep[rev[v]]-2*dep[LCA(rev[u],rev[v])];
}
void add(int pos,int color) {
if(c[color].size()==0) {
c[color].insert(pos);ans_c[color]=0;
return ;
}
auto p=c[color].lower_bound(pos);
if(p==c[color].begin()||p==c[color].end()) {
auto x=c[color].begin();auto y=c[color].rbegin();
ans_c[color]+=(get_dist(pos,*x)+get_dist(pos,*y)-get_dist(*x,*y))/2;
}
else {
auto x=p;auto y=p;x--;
ans_c[color]+=(get_dist(pos,*x)+get_dist(pos,*y)-get_dist(*x,*y))/2;
}
c[color].insert(pos);
}
void del(int pos,int color) {
if(c[color].size()==1) {
c[color].erase(pos);ans_c[color]=-1;
return ;
}
c[color].erase(pos);
auto p=c[color].lower_bound(pos);
if(p==c[color].begin()||p==c[color].end()) {
auto x=c[color].begin();auto y=c[color].rbegin();
ans_c[color]-=(get_dist(pos,*x)+get_dist(pos,*y)-get_dist(*x,*y))/2;
}
else {
auto x=p;auto y=p;x--;
ans_c[color]-=(get_dist(pos,*x)+get_dist(pos,*y)-get_dist(*x,*y))/2;
}
}
int main() {
n=read();
for(int i=1;i<=n-1;i++) {
int u=read(),v=read();
edge[u].push_back(v);
edge[v].push_back(u);
}
memset(ans_c,-1,sizeof(ans_c));
dfs1(1,0);dfs2(1,1);
for(int i=1;i<=n;i++) {
a[i]=read();
add(dfsn[i],a[i]);
}
int q=read();
for(int i=1;i<=q;i++) {
string opt;cin>>opt;
if(opt=="Q") {
int color=read();
printf("%d\n",ans_c[color]);
}
else {
int pos=read(),color=read();
del(dfsn[pos],a[pos]);
add(dfsn[pos],color);a[pos]=color;
}
}
return 0;
}