目录
- 一、对抗训练
- FGM(Fast Gradient Method): ICLR2017
- 代码实现
- 二、权值平均
- 1.指数移动平均(Exponential Moving Average,EMA)
- 为什么EMA会有效?
- 代码实现
- 2. 随机权值平均(Stochastic Weight Averaging,SWA)
- SWA实现
- 使用swa模板
- 三、训练加速
- 1.混合精度(amp)
- 为什么要使用AMP?
- 使用方法
- 2. 数据并行(Data Parallel, DP和Distributed Data Parallel,DDP)
- 代码实现
- 四、显卡不够用怎么增大batch size
- 梯度累加法
- 代码实现
一、对抗训练
对抗训练是一种引入噪声的训练方式,可以对参数进行正则化,提升模型鲁棒性和泛化能力。对抗训练的假设是:给输入加上扰动之后,输出分布和原Y的分布一致。

θ尖是常数,目的是在计算对抗扰动时虽然计算了梯度,但不对参数进行更新,因为当前得到的对抗扰动是对旧参数最优的。
**用一句话形容对抗训练的思路,就是在输入上进行梯度上升(增大loss),在参数上进行梯度下降(减小loss)。**由于输入会进行embedding lookup(embedding lookup从字面意思上讲,就是查找对应的embedding),所以实际的做法是在embedding table上进行梯度上升。
FGM(Fast Gradient Method): ICLR2017
FGM是根据具体的梯度进行scale,得到更好的对抗样本。假设对于输入的梯度为:
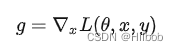
其扰动为:
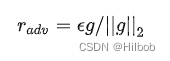
伪代码:对于每个x:
1.计算x的前向loss、反向传播得到梯度
2.根据embedding矩阵的梯度计算出r,并加到当前embedding上,相当于x+r
3.计算x+r的前向loss,反向传播得到对抗的梯度,累加到(1)的梯度上
4.将embedding恢复为(1)时的值
5.根据(3)的梯度对参数进行更新
代码实现
class FGM(object):
def __init__(self, module):
self.module = module
self.backup = {}
# 记得这里的embedding名字设置为自己网络的
def attack(self,epsilon=1.,emb_name='word_embeddings'):
for name, param in self.module.named_parameters():
if param.requires_grad and emb_name in name and "video_embeddings" not in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self,emb_name='word_embeddings'):
for name, param in self.module.named_parameters():
if param.requires_grad and emb_name in name and "video_embeddings" not in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
二、权值平均
1.指数移动平均(Exponential Moving Average,EMA)
假设我们有n个数据:
[
θ
1
,
θ
2
,
θ
3
,
.
.
.
θ
n
]
[θ_1,θ_2,θ_3,...θ_n]
[θ1,θ2,θ3,...θn]
普通的平均数为:
EMA为: 其中,
v
t
v_t
vt表示前
t
t
t条的平均值 (
v
0
=
0
v_0=0
v0=0),
β
β
β是加权权重值 (一般设为0.9-0.999)。
其中,
v
t
v_t
vt表示前
t
t
t条的平均值 (
v
0
=
0
v_0=0
v0=0),
β
β
β是加权权重值 (一般设为0.9-0.999)。
在深度学习的优化过程中,
θ
t
θ_t
θt是
t
t
t时刻的模型权重weights,
v
t
v_t
vt是t时刻的影子权重(shadow weights)。**在梯度下降的过程中,会一直维护着这个影子权重,但是这个影子权重并不会参与训练。**基本的假设是,模型权重在最后的n步内,会在实际的最优点处抖动,所以我们取最后n步的平均,能使得模型更加的鲁棒。
为什么EMA会有效?
对于EMA,有如下计算:

而对于普通的权值计算:
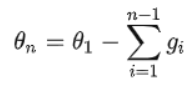
可见,普通的参数权重相当于一直累积更新整个训练过程的梯度,使用EMA的参数权重相当于使用训练过程梯度的加权平均(即对第i步的梯度下降增加了权重系数
1
−
α
n
−
i
1-α^{n-i}
1−αn−i,因此刚开始的梯度权值很小)。由于刚开始训练不稳定,得到的梯度给更小的权值更为合理,所以EMA会有效。
代码实现
class EMA():
def __init__(self, model, decay):
self.model = model
self.decay = decay
self.shadow = {}
self.backup = {}
def register(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
self.shadow[name] = param.data.clone()
def update(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
assert name in self.shadow
new_average = (1.0 - self.decay) * param.data + self.decay * self.shadow[name]
self.shadow[name] = new_average.clone()
def apply_shadow(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
assert name in self.shadow
self.backup[name] = param.data
param.data = self.shadow[name]
def restore(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
# 初始化
ema = EMA(model, 0.999)
ema.register()
# 训练过程中,更新完参数后,同步update shadow weights
def train():
optimizer.step()
ema.update()
# eval前,apply shadow weights;eval之后,恢复原来模型的参数
def evaluate():
ema.apply_shadow()
# evaluate
ema.restore()
2. 随机权值平均(Stochastic Weight Averaging,SWA)
深度学习模型会收敛到不同的局部最小值,而区别这些局部最小值好坏的一个标准就是所谓的泛化能力。我们训练的模型经常存在一个现象,我们训练模型会存储很多的 checkpoints。不同的 checkpoints 的表现是有差异的,它们在大部分的 case 上表现几乎一致,但是在个别 case 上有差异,比如 checkpoint1 在 A case 上效果好,但是在 B case 上效果一般,相反 checkpoint2 在 B case 上效果较好,而在 A case 上效果一般。这是因为这些 checkpoints 实际上是收敛于不同的局部最小值导致的,因为深度学习模型永远也不会收敛到全局最小值的,但是那些较为平坦的 局部最小值 趋向于有更好的泛化能力,SWA就是一种得到较为平坦的 局部最小值的方法。
SWA是利用随机梯度下降法就能够提升深度学习模型的泛化能力的方法,而且不需要多余的代价,而且在Pytorch里面可以作为一种即插即用的方法来代替任何的优化器,SWA有广泛的应用和如下特点:
1.实验证明SWA能够显著的提高视觉任务的泛化能力,以 CIFAR 和 ImageNet 数据集为基准,提高了 VGG、ResNets、WideResNets 和 DenseNets 的泛化能力。
2.SWA 在半监督学习和域适应的关键基准数据集上达到了SOTA 效果。
3.在深度强化学习中 SWA 能够提高训练的稳定性,也提高了策略梯度法的最终平均奖励。
4.SWA在深度学习的扩展应用包括有效的贝叶斯模型的平均,也是高质量不确定性估计和校准
5.SWA用于低精度的训练(SWALP),甚至在所有的数值都量化到 8 位的情况下也能够比肩全精度的 SGD 的性能,包括梯度累加器。
简言之,SWA 就是对通过可调整的学习率的SGD算法得到的多个权重进行平均的方法。SWA最终的结果就是在一个广阔的平坦的 loss 区域的中心,而SGD趋向于收敛到低loss区域的边界,这使得结果容易受到训练和测试误差平面之间转换的影响,即在低loss区域的边界可能在测试集合误差平面较大的位置,也就是模型不够鲁棒。
SWA实现
有两个让SWA能够work的重要因素:
1.第一个是**可调整的学习率能让 SGD 继续探索高性能网络权重的集合而不是简单的只收敛到一个解上。**这块的理论实际上是不同的局部最小值是包含不同的有用信息的。例如:我们可以先用标准的衰减学习率策略在前75%的训练时间里进行学习,然后再把学习率设定到一个合理的较大的常数学习率上,在剩余的25%的训练时间里学习,这样就得到了很多的ckpt。
2.第二个是对通过SGD得到的不同 ckpt 的权重值进行平均。例如我们维持一个滑动平均的权重,在剩余的25%的训练时间里每个epoch都进行累计平均。
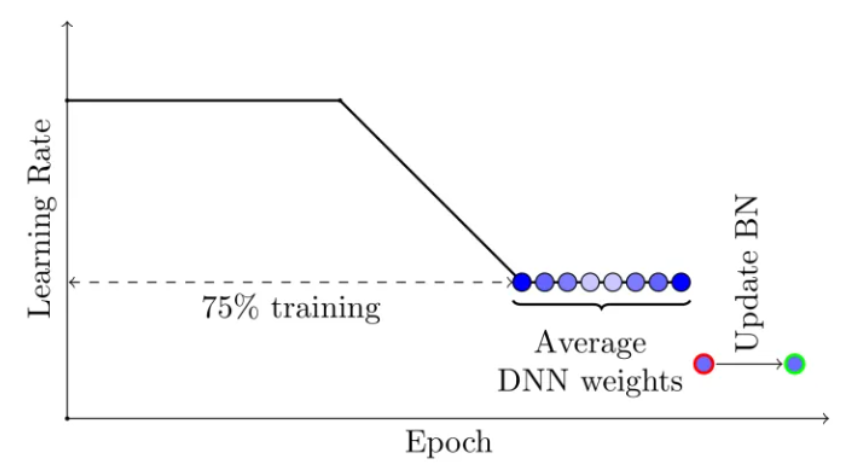
上图就是用标准的衰减学习率策略在前75%的训练时间里进行学习,然后再把学习率设定到一个合理的较大的常数学习率上,在剩余的25%的训练时间里学习。SWA的平均在最后的25%的训练时间里面产生。
使用swa模板
from torch.optim.lr_scheduler import CosineAnnealingLR
from torch import optim
import torchcontrib
base_opt = optim.Adam(net.parameters(), lr=0.015, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
optimizer = torchcontrib.optim.SWA(base_opt) # for SWA
scheduler = CosineAnnealingLR(base_opt, T_max=20)
...
scheduler.step()
# 定义什么时候开始取平均
if epoch % 100 == 0:
optimizer.swap_swa_sgd()
三、训练加速
1.混合精度(amp)
为什么要使用AMP?
AMP其实就是Float32与Float16的混合,那为什么不单独使用Float32或Float16,而是两种类型混合呢?原因是:在某些情况下Float32有优势,而在另外一些情况下Float16有优势。
FP16优势有三个:
1 .减少显存占用;
2.加快训练和推断的计算,能带来多倍速的体验;
3,张量核心的普及(NVIDIA TensorCore) ,低精度计算是未来深度学习的一个重要趋势。
而FP16也带来了些问题:
1.溢出错误:由于 FP16 的动态范围比 FP32 的动态范围要狭窄很多,因此在计算过程中很容易出现上溢出(Overflow,g>65504)和下溢出(Underflow,)的错误,溢出之后就会出现“Nan”的问题。在深度学习中,由于激活函数的的梯度往往要比权重梯度小,更易出现下溢出的情况。
2.舍入误差:舍入误差指的是当梯度过小,小于当前区间内的最小间隔时,该次梯度更新可能会失败。
解决FP16问题的办法:混合精度训练+动态损失放大
1.混合精度训练(Mixed Precision): 混合精度训练的精髓在于“在内存中用 FP16 做储存和乘法从而加速计算,用 FP32做累加避免舍入误差”。混合精度训练的策略有效地缓解了舍入误差的问题。
2.损失放大(Loss Scaling): 即使用了混合精度训练,还是会存在无法收敛的情况,原因是激活梯度的值太小,造成了下溢出(Underflow)。损失放大的思路是:反向传播前,将损失变化(dLoss)手动增大,因此反向传播时得到的中间变量(激活函数梯度)则不会溢出;反向传播后,将权重梯度缩小倍,恢复正常值。
动态损失放大(Dynamic Loss Scaling)
AMP 默认使用动态损失放大,为了充分利用 FP16 的范围,缓解舍入误差,尽量使用最高的放大倍数,如果产生了上溢出(Overflow),则跳过参数更新,缩小放大倍数使其不溢出,在一定步数后(比如 2000 步)会再尝试使用大的 scale 来充分利用 FP16 的范围
使用方法
在前向传播中使用@autocast装饰器即可调用amp混合精度,torch.cuda.amp
# 导入python包
from torch.cuda.amp import autocast, GradScaler
# 采用以下两种方式对forward使用amp
# 方式一:设置autocast区域
class Mymodel(nn.Module):
...
def forward(self, input):
with autocast():
...
# 方式二:使用autocast装饰器
class Mymodel(nn.Module):
...
@autocast()
def forward(self, input):
...
model=Mymodel().cuda()
optimizer=optim.SGD(model.parameters(),...)
# 在训练最开始之前实例化一个GradScaler对象
scaler = GradScaler()
# Runs the forward pass with autocasting.
for epoch in range(epochs):
for i, (data, label) in enumerate(loader):
with autocast(enabled=args.amp):
model.train()
loss = model(batch)
loss = loss.mean()
# 1、Scales loss. 先将梯度放大 防止梯度消失
scaler.scale(loss).backward()
# 2、scaler.step() 再把梯度的值unscale回来.
# 如果梯度的值不是 infs 或者 NaNs, 那么调用optimizer.step()来更新权重,
# 否则,忽略step调用,从而保证权重不更新(不被破坏)
scaler.step(optimizer)
# 3.Updates the scale for next iteration.
scaler.update()
scheduler.step()
optimizer.zero_grad()
2. 数据并行(Data Parallel, DP和Distributed Data Parallel,DDP)
这里简单说下DP。DDP可参考Pytorch 并行训练(DP, DDP)的原理和应用
并行训练可以分为数据并行和模型并行。
1.模型并行:模型并行主要应用于模型相比显存来说更大,一块 device 无法加载的场景,通过把模型切割为几个部分,分别加载到不同的 device 上。比如早期的 AlexNet,当时限于显卡,模型就是分别加载在两块显卡上的。
2.数据并行:这个是日常会应用的比较多的情况。每一个 device 上会加载一份模型,然后把数据分发到每个 device 并行进行计算,加快训练速度。
代码实现
model = torch.nn.parallel.DataParallel(model.to(args.device))
四、显卡不够用怎么增大batch size
参考聊聊梯度累加
梯度累加法
梯度累加,顾名思义,就是将多次计算得到的梯度值进行累加,然后一次性进行参数更新。假设我们有batch size = 256的global-batch,在单卡训练显存不足时,将其分为多个小的mini-batch(如分为大小为64的4个mini-batch),每个step送入1个mini-batch获得梯度,将多次获得的梯度进行累加后再更新参数,以次达到模拟单次使用global-batch训练的目的。
简单来说:时间换空间。加长训练时间,来换取大batch在小设备上可训练。

代码实现
# batch accumulation parameter
accum_iter = 4
# loop through enumaretad batches
for batch_idx, (inputs, labels) in enumerate(data_loader):
# forward pass
preds = model(inputs)
loss = criterion(preds, labels)
# scale the loss to the mean of the accumulated batch size
loss = loss / accum_iter
# backward pass
loss.backward()
# weights update
if ((batch_idx + 1) % accum_iter == 0) or (batch_idx + 1 == len(data_loader)):
optimizer.step()
optimizer.zero_grad()


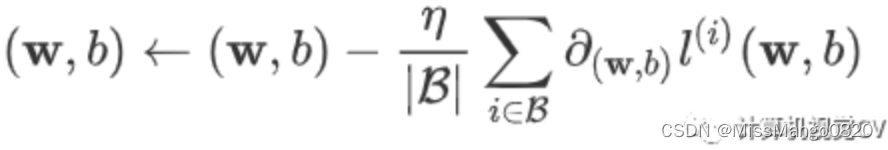

![English Learning - L2 第 3 次小组纠音 [ʌ] [ɒ] [ʊ] [ɪ] [ə] [e] 2023.3.4 周六](https://img-blog.csdnimg.cn/f15da8f7f9314c5ba02ec2c5dd42978b.png)


![[数据结构与算法(严蔚敏 C语言第二版)]第1章 绪论(学习复习笔记)](https://img-blog.csdnimg.cn/dd1bb8c16e3f4cc8908ea592ae7d3c8b.png)
