本文主要参考 ¹’ ²’ ³

更新：2023 / 3 / 1

---

---

先通过下面的方式确认 Pytorch 已经被正确地安装到你的电脑上，

import torch
torch.manual_seed(0)
torch.cuda.manual_seed(0)

print(torch.__version__)								// 输出pytorch的版本号
# 1.13.1

---

创建

1. 创建一个 5 x 3 的未初始化的 Tensor：

tensor1 = torch.empty(5,3)
# tensor([[0.0000e+00, 0.0000e+00, 0.0000e+00],
#         [0.0000e+00, 0.0000e+00, -0.0000e+00],
#         [0.0000e+00, 0.0000e+00, 0.0000e+00],
#         [1.4013e-45, 0.0000e+00, 0.0000e+00],
#         [0.0000e+00, 0.0000e+00, 0.0000e+00]])

2. 创建一个 5x3 的随机初始化的 Tensor:

tensor2 = torch.rand(5,3)
# tensor([[0.1898, 0.4211, 0.0858],
#         [0.8893, 0.1100, 0.4439],
#         [0.3058, 0.6456, 0.3877],
#         [0.4485, 0.0570, 0.3891],
#         [0.6083, 0.0609, 0.2034]])

3. 创建一个 5x3 的 long 型全 0 的 Tensor：

tensor3 = torch.zeros(5,3, dtype=torch.long)
# tensor([[0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0]])

4. 直接根据数据创建

tensor4 = torch.tensor([5.5, 3])
# tensor([5.5000, 3.0000])

5. 通过现有的 Tensor 来创建，此方法会默认重用输入 Tensor 的一些属性。

tensor5 = torch.zeros(5, 3, dtype=torch.long)
# tensor([[0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0]])
#
# <class 'torch.Tensor'>
#
# torch.int64
#
# cpu


tensor5 = tensor3.new_ones(5, 3, dtype=torch.float64)      
# tensor([[1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.]], dtype=torch.float64)
#
# <class 'torch.Tensor'>
#
# torch.float64
#
# cpu


tensor5 = torch.randn_like(tensor3, dtype=torch.float)
# tensor([[ 9.8904e-01,  3.8009e-01, -1.5320e-03],
#         [-7.3697e-01, -1.6366e+00, -4.0838e-02],
#         [-3.4675e-01,  2.5153e+00,  5.3277e-01],
#         [-1.5581e+00,  3.5077e-01,  7.3052e-01],
#         [-1.9839e+00,  6.9044e-01,  7.0959e-01]])
#
# <class 'torch.Tensor'>
#
# torch.float32
#
# cpu

---

操作

算术操作

加法

1. x+y

x = torch.rand(5, 3)
# tensor([[0.3004, 0.9549, 0.5942],
#         [0.5424, 0.8032, 0.5955],
#         [0.7312, 0.1777, 0.4129],
#         [0.3030, 0.4114, 0.8384],
#         [0.1771, 0.9954, 0.1406]])

y = torch.rand(5, 3)
# tensor([[0.7122, 0.9141, 0.4856],
#         [0.7774, 0.5033, 0.6968],
#         [0.4215, 0.9920, 0.4468],
#         [0.4443, 0.4337, 0.7687],
#         [0.1705, 0.5133, 0.2859]])

sum = x + y
# tensor([[1.0126, 1.8690, 1.0799],
#         [1.3198, 1.3065, 1.2924],
#         [1.1527, 1.1697, 0.8597],
#         [0.7474, 0.8451, 1.6071],
#         [0.3475, 1.5087, 0.4265]])

2. torch.add(x+y)

x = torch.rand(5, 3)
# tensor([[0.9455, 0.2307, 0.7058],
#         [0.1013, 0.2585, 0.1135],
#         [0.0834, 0.1876, 0.6470],
#         [0.0526, 0.3814, 0.6729],
#         [0.5239, 0.7080, 0.2696]])

y = torch.rand(5, 3)
# tensor([[0.2314, 0.0348, 0.7387],
#         [0.2778, 0.8723, 0.3599],
#         [0.8507, 0.5841, 0.0185],
#         [0.7318, 0.6347, 0.5771],
#         [0.3608, 0.7299, 0.9747]])

sum = torch.add(x, y)
# tensor([[1.1768, 0.2655, 1.4445],
#         [0.3791, 1.1308, 0.4734],
#         [0.9342, 0.7717, 0.6655],
#         [0.7844, 1.0161, 1.2500],
#         [0.8847, 1.4379, 1.2443]])

或者，

x = torch.rand(5, 3)
# tensor([[0.7198, 0.1457, 0.2093],
#         [0.6683, 0.8254, 0.0505],
#         [0.8574, 0.1102, 0.5093],
#         [0.4496, 0.4313, 0.6737],
#         [0.6938, 0.2051, 0.5161]])

y = torch.rand(5, 3)
# tensor([[0.2923, 0.7317, 0.6552],
#         [0.7680, 0.7655, 0.2276],
#         [0.1741, 0.7202, 0.4799],
#         [0.0494, 0.8067, 0.1426],
#         [0.5097, 0.9381, 0.8655]])

result = torch.empty(5, 3)
torch.add(x, y, out=result)
# tensor([[1.0121, 0.8774, 0.8645],
#         [1.4363, 1.5909, 0.2781],
#         [1.0315, 0.8304, 0.9893],
#         [0.4990, 1.2379, 0.8163],
#         [1.2035, 1.1432, 1.3816]])

3. y.add_(x)

x = torch.rand(5, 3)
# tensor([[0.6877, 0.7691, 0.8871],
#         [0.4104, 0.2438, 0.4188],
#         [0.7285, 0.8033, 0.1320],
#         [0.1622, 0.5556, 0.1193],
#         [0.6330, 0.6507, 0.2798]])

y = torch.rand(5, 3)
# tensor([[0.6695, 0.8028, 0.8364],
#         [0.2491, 0.7611, 0.6267],
#         [0.5496, 0.1332, 0.4203],
#         [0.6156, 0.8650, 0.2299],
#         [0.1354, 0.7796, 0.3397]])

sum = y.add_(x)
# tensor([[1.3572, 1.5719, 1.7235],
#         [0.6595, 1.0049, 1.0454],
#         [1.2781, 0.9365, 0.5523],
#         [0.7777, 1.4206, 0.3493],
#         [0.7683, 1.4303, 0.6195]])

索引

x = torch.rand(5, 3)
# tensor([[0.7302, 0.3153, 0.1036],
#         [0.6712, 0.1971, 0.0408],
#         [0.4045, 0.8566, 0.6853],
#         [0.6205, 0.7717, 0.3650],
#         [0.1714, 0.8397, 0.6293]])

y = x[0, :]								// 引用源tensor的第一行
# tensor([0.7302, 0.3153, 0.1036])
y += 1
# tensor([1.7302, 1.3153, 1.1036])
#
# torch.Size([3])

print(x)								// # 源tensor也被改了
# tensor([[1.7302, 1.3153, 1.1036],
#         [0.6712, 0.1971, 0.0408],
#         [0.4045, 0.8566, 0.6853],
#         [0.6205, 0.7717, 0.3650],
#         [0.1714, 0.8397, 0.6293]])

形状

查询形状

可以通过 shape 或者 size() 来获取 Tensor，比如 tensor1 的形状:

print(tensor1.size())
print(tensor1.shape)

输出为：

torch.Size([5, 3])
torch.Size([5, 3])

注意：返回的 torch.Size 的数据类型是 <class 'torch.Size'>，可以像 tuple 对其进行操作。

改变形状

用 view() 来改变 Tensor 的形状：

x = torch.rand(5, 3)
# tensor([[0.4086, 0.6557, 0.1230],
#         [0.0248, 0.0442, 0.0657],
#         [0.1682, 0.8937, 0.3877],
#         [0.5520, 0.0309, 0.1907],
#         [0.0817, 0.9466, 0.7049]])
        
y = x.view(15)
# tensor([0.4086, 0.6557, 0.1230, 0.0248, 0.0442, 0.0657, 0.1682, 0.8937, 0.3877,
#         0.5520, 0.0309, 0.1907, 0.0817, 0.9466, 0.7049])
#
# torch.Size([15])

z = x.view(-1, 5)
# tensor([[0.4086, 0.6557, 0.1230, 0.0248, 0.0442],
#         [0.0657, 0.1682, 0.8937, 0.3877, 0.5520],
#         [0.0309, 0.1907, 0.0817, 0.9466, 0.7049]])
# 
# torch.Size([3, 5])

此时如果对 x 操作，y 的值也是会跟着变的，如下所示：

x += 1
# tensor([[1.4086, 1.6557, 1.1230],
#         [1.0248, 1.0442, 1.0657],
#         [1.1682, 1.8937, 1.3877],
#         [1.5520, 1.0309, 1.1907],
#         [1.0817, 1.9466, 1.7049]])

print(y)
# tensor([1.4086, 1.6557, 1.1230, 1.0248, 1.0442, 1.0657, 1.1682, 1.8937, 1.3877,
#         1.5520, 1.0309, 1.1907, 1.0817, 1.9466, 1.7049])

如果不想共享内存，推荐先用 clone 创造一个副本然后再使用 view。

x_cp = x.clone().view(15)
# tensor([1.4086, 1.6557, 1.1230, 1.0248, 1.0442, 1.0657, 1.1682, 1.8937, 1.3877,
#         1.5520, 1.0309, 1.1907, 1.0817, 1.9466, 1.7049])

x -= 1
# tensor([[0.4086, 0.6557, 0.1230],
#         [0.0248, 0.0442, 0.0657],
#         [0.1682, 0.8937, 0.3877],
#         [0.5520, 0.0309, 0.1907],
#         [0.0817, 0.9466, 0.7049]])

广播机制

在 Pytorch 中，两个张量形状不同有时也可以进行运算，这涉及到了 Pytorch 中的广播机制，也就是 Pytorch 会自动扩充两个张量，使两个张量的形状相同，然后再进行运算。

下面具体说明 ⁴’ ⁵：

广播条件

如果两个张量满足下面两个条件，就可以广播：

• 每个张量都至少有一个维度；

x=torch.empty((0,))						  # 不能广播，因为两个张量都必须只有一个维度
y=torch.empty(2,2)

• 对两个张量的维度从后往前处理，维度的大小（这个维度的长度）必须要么相等，要么其中一个为 1，或者其中一个张量后面不存在维度了。

x=torch.empty(5,7,3)					  # 可以广播，对于相同的形状
y=torch.empty(5,7,3)

x=torch.empty(5,3,4,1)					
y=torch.empty(  3,1,1)					  # 可以广播，倒数第一个维度相等，倒数第二个维度不等但其中一个为1，倒数第三个维度相等；

x=torch.empty(3,2,4,1)	
y=torch.empty(  3,1,1)					  # 不能广播，倒数第一个维度相等，倒数第二个维度不等但其中一个为1，倒数第三个维度不等且无1

运算

如果两个张量 x，y 是可广播的，结果的张量大小按如下方式计算：

• 如果 x 和 y 的维度数量不同，对维度数量少的张量增加新的维度，且维度大小为 1，使得两个张量的维度数量相同。
• 对每个维度，结果的维度大小是 x 和 y 的维度大小的最大值。（其实如果某个维度大小不同，那么有一个维度大小肯定是 1 ）

下面举几个例子，

x=torch.empty(5,1,4,1)
y=torch.empty(  3,1,1)
(x+y).size()
# torch.Size([5, 3, 4, 1])

x=torch.empty(1)
y=torch.empty(3,1,7)
(x+y).size()
# torch.Size([3, 1, 7])

x=torch.empty(5,2,4,1)
y=torch.empty(3,1,1)
(x+y).size()
# RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 1

---

数据类型转换

Tensor转NumPy

以下面的名为 x 的 tensor 为例，

x = torch.ones(5)
y = x.numpy()

print(x)
print(type(x))
# tensor([1., 1., 1., 1., 1.])
# <class 'torch.Tensor'>

print(y)
print(type(y))
# [1. 1. 1. 1. 1.]
# <class 'numpy.ndarray'>

下面，开始转换：

x += 1

print(x)
print(type(x))
# tensor([2., 2., 2., 2., 2.])
# <class 'torch.Tensor'>

print(y)
print(type(y))
# [2. 2. 2. 2. 2.]
# <class 'numpy.ndarray'>

y += 1

print(x)
print(type(x))
# tensor([3., 3., 3., 3., 3.])
# <class 'torch.Tensor'>

print(y)
print(type(y))
# [3. 3. 3. 3. 3.]
# <class 'numpy.ndarray'>

NumPy转Tensor

以下面的名为 x 的 numpy.ndarray 为例，

x = np.ones(5)
y = torch.from_numpy(x)

print(x)
print(type(x))
# [1. 1. 1. 1. 1.]
# <class 'numpy.ndarray'>

print(y)
print(type(y))
# tensor([1., 1., 1., 1., 1.], dtype=torch.float64)
# <class 'torch.Tensor'>

下面，开始转换，

x += 1

print(x)
print(type(x))
# [2. 2. 2. 2. 2.]
# <class 'numpy.ndarray'>

print(y)
print(type(y))
# tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
# <class 'torch.Tensor'>

y += 1

print(x)
print(type(x))
# [3. 3. 3. 3. 3.]
# <class 'numpy.ndarray'>

print(y)
print(type(y))
# tensor([3., 3., 3., 3., 3.], dtype=torch.float64)
# <class 'torch.Tensor'>

---

线性回归

简单的说，线性回归预测是基于某个变量 X （自变量）来预测变量 Y（因变量）的值，当然前提是 X 和 Y 之间存在线性关系。这两个变量之间的线性关系可以用直线表示（称为回归线）⁶。

线性回归的基本要素

1. 模型

举个预测波士顿房价的例子，这里我们都进行了化简：假设房屋价格只取决于两个因素，即 面积（平方米）和 房龄（年）。
接下来我们希望探索价格与这两个因素的具体关系。线性回归假设输出与各个输入之间是线性关系:

2. 数据集

我们收集一系列的真实数据，例如多栋房屋的真实价格和对应的面积、房龄。我们希望在这个数据集上面来拟合模型参数使模型的预测价格与真实价格的误差达到最小。
在 ML 术语中，数据集被称为 训练集（ training set ），一栋房屋被称为一个样本（ sample ），其真实售出价格叫作标签（ label ），用来预测标签的两个因素叫作特征（ feature ）。

3. 损失函数

在模型训练中，我们需要计算价格预测值与真实值之间的误差。一个常用的选择是平方函数。它在评估索引为的样本误差的表达式为：

4. 优化函数 - 随机梯度下降

当模型和损失函数形式较为简单时，误差最小化问题的解可以直接用公式表达出来，这类解叫作 解析解（ analytical solution ）。
本节使用的线性回归和平方误差刚好属于这个范畴。

还有一类模型并没有解析解，只能通过优化算法有限次迭代来尽可能降低损失函数的值。这类解叫作 数值解（ numerical solution ）。

求数值解的优化算法中，小批量随机梯度下降（ mini-batch stochastic gradient descent ）在深度学习中被广泛使用。先初始化模型参数的初始值；然后对参数进行多次迭代，使每次迭代都降低损失函数的值。
在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（ mini-batch ），然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

学习率：代表在每次优化中，能够学习的步长的大小
批量大小：是小批量计算中的批量大小 batch size

线性回归模型从零开始的实现

数据集

生成数据集

使用线性模型来生成数据集，生成一个 1000 个样本的数据集，下面是用来生成数据的线性关系：

import torch
from matplotlib import pyplot as plt
import numpy as np
import random

# set input feature number: 1. 'area'; 2. 'age';
num_inputs = 2

# set example number: 1000 sample, or, 1000 prices;
num_examples = 1000

# set true weight and bias in order to generate corresponded label: 
# 1. 'Warea' & 'Wage'; 
# 2. 'b';
true_w = [2, -3.4]
true_b = 4.2

# generate a area and age tensor with torch.Size([1000, 2]);
features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
# tensor([[-1.2659,  1.3218],
#         [-1.3461, -0.3002],
#         [ 0.6401,  2.2983],
#         ...,
#         [-0.5203,  0.5586],
#         [ 0.0712, -0.3995],
#         [-0.2995,  1.1682]])


# generate 1000 samples, following the model below:
# price = Warea    * area           + Wage      * age            + b
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
# tensor([-2.8260e+00,  2.5284e+00, -2.3339e+00,  3.1779e+00,  2.3752e+00,
#          1.4073e+01,  2.1673e+00,  8.4260e-01,  7.1728e+00, -7.0487e-01,
# ...
#         3.1599e+00, 1.0972e+01, 1.4133e+01, 5.6141e+00, 6.6164e+00,
#         3.2544e+00, 3.9535e+00, 1.2600e+00, 5.7006e+00, -3.7077e-01])

# generate a random seed array with (1000, ) size;
seeds = np.random.normal(0, 0.01, size=labels.size())
# [ 8.88058964e-03  3.53739524e-03  7.70576446e-03 -7.14245925e-03
#  -6.22237319e-03  1.07257943e-02  4.48531221e-03 -3.44305054e-03
# ...
#   - 6.88459456e-03  4.02737440e-03 - 1.95810746e-03 - 7.32376821e-03
#   3.46941304e-03  2.14670627e-03  1.32788726e-02  1.40899248e-02]

# apply seed array on previously generated labels tensor;
labels += torch.tensor(seeds, dtype=torch.float32)
# tensor([-2.8172e+00,  2.5319e+00, -2.3262e+00,  3.1708e+00,  2.3690e+00,
#          1.4084e+01,  2.1717e+00,  8.3915e-01,  7.1672e+00, -7.0108e-01,
# ...
#         3.1597e+00, 1.0975e+01, 1.4126e+01, 5.6181e+00, 6.6144e+00,
#         3.2471e+00, 3.9570e+00, 1.2621e+00, 5.7139e+00, -3.5668e-01])

使用 散点图 来呈现上面所生成的数据，如下所示：

# plot with age as x, price as y
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1)
plt.show()

读取数据集

def data_iter(batch_size, features, labels):
    '''
    :param batch_size: size for a batch of data;
    :param features: an area and age tensor with torch.Size([1000, 2]);
    :param labels: price;
    :return:
    '''
    num_examples = len(features)                        # 1000个samples对应1000组features
    indices = list(range(num_examples))                 # 1000个samples的初始索引值为[0, 1, ..., 998, 999]
    random.shuffle(indices)                             # 1000个samples的索引值被打乱后为[19, 711, ..., 796, 684, 708, 929, 721, 479, 864, 722, 548, 23]
    for i in range(0, num_examples, batch_size):        # 在indices的列表范围中按序每次抽取10个索引值
        j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)])  # the last time may be not enough for a whole batch
        # 最后一组被抽取到的10个索引值所组成的张量组为tensor([796, 684, 708, 929, 721, 479, 864, 722, 548, 23])，数据类型为<class 'torch.Tensor'>，张量大小为torch.Size([10])
        yield features.index_select(0, j), labels.index_select(0, j)
        # 按照最后一组10个索引值，对features和labels这两个张量进行索引匹配，所得到的张量如下，大小分别为torch.Size([10, 2]) torch.Size([10])
        # tensor([[1.6381, 0.5704],
        #         [0.0539, -0.4795],
        #         [-0.2489, 0.3873],
        #         [-0.2030, 0.7919],
        #         [0.6328, 0.8435],
        #         [0.1003, -0.2580],
        #         [0.6470, 1.7876],
        #         [0.6788, -1.7129],
        #         [0.6362, -1.2819],
        #         [0.5954, -1.0731]])
        # tensor([5.5395, 5.9433, 2.3960, 1.1101, 2.6187, 5.2781, -0.5657, 11.3878,
        #         9.8319, 9.0328])

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)

indices 是 1000 个 sample 值的索引序列。
先使用 random.shuffle 将索引序列 indices 打乱，然后在 [0, 1000] 这个范围内每 10 个为一组对被打乱的 indices 进行按序抽取。再根据抽取到的 10 个索引值，对 features 和 labels 这两个 tensor 进行按索引值进行映射，生成 features.index_select(0, j) 和 labels.index_select(0, j)。

初始化模型参数

num_inputs = 2

w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
# tensor([[-0.0064],
#         [-0.0057]])
# torch.Size([2, 1])

b = torch.zeros(1, dtype=torch.float32)
# tensor([0.])
# torch.Size([1])

w.requires_grad_(requires_grad=True)
# tensor([[-0.0064],
#         [-0.0057]], requires_grad=True)
# torch.Size([2, 1])

b.requires_grad_(requires_grad=True)
# tensor([0.], requires_grad=True)
# torch.Size([1])

通过 num_inputs 确定 features 有 2 个。再通过 require_grad=True ⁷’ ⁸ 表示需要计算 Tensor 的梯度，告诉自动求导开始记录对 Tensor 的操作。

requires_grad=False 可以用来冻结部分网络，只更新另一部分网络的参数。

定义模型

定义用来训练参数的训练模型：

def linreg(X, w, b):    

return torch.mm(X, w) + b

定义损失函数

我们使用的是 均方误差损失 函数，如下所示：

def squared_loss(y_hat, y): 
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

定义优化函数

在这里优化函数使用的是 小批量随机梯度下降：

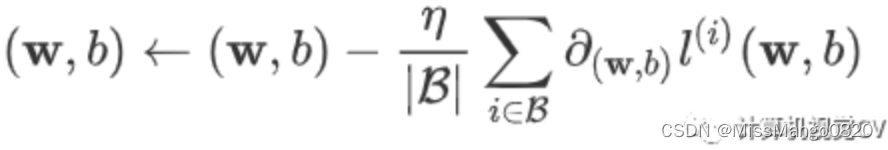
def sgd(params, lr, batch_size): 
    for param in params:
        param.data -= lr * param.grad / batch_size

训练

lr = 0.03
num_epochs = 5                  # 定义训练次数

net = linreg                    # 初始化模型
loss = squared_loss             # 初始化损失函数

# 开始训练
for epoch in range(num_epochs):                             # 在每次训练中，dataset中的所有samples只呗使用一次
    for X, y in data_iter(batch_size, features, labels):    # X代表小批量数据中的features, y代表小批量数据中的labels
        l = loss(net(X, w, b), y).sum()                     # 计算小批量数据损失的gradient
        l.backward()
        sgd([w, b], lr, batch_size)                         # 使用w和b来迭代模型中的参数
        w.grad.data.zero_()                                 # 将模型参数的gradient重置为0
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
# epoch 1, loss 0.026009
# epoch 2, loss 0.000095
# epoch 3, loss 0.000049
# epoch 4, loss 0.000049
# epoch 5, loss 0.000049

线性回归模型使用pytorch的简洁实现

数据集

生成数据集

import torch
from torch import nn
import numpy as np

torch.manual_seed(1)                                    # 设置CPU生成随机数的种子，方便下次复现
torch.set_default_tensor_type('torch.FloatTensor')      # 设置pytorch中默认的浮点类型

num_inputs = 2
num_examples = 1000

true_w = [2, -3.4]
true_b = 4.2

features = torch.randn(num_examples, num_inputs, dtype=torch.float32)

# price = Warea    * area           + Wage      * age            + b
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
seeds = np.random.normal(0, 0.01, size=labels.size())
labels += torch.tensor(seeds, dtype=torch.float32)

在这里，生成数据集 跟 线性回归模型从零开始的实现 的 生成数据集 的实现中是完全一样的。

torch.manual_seed() 的用法参考此处 ⁹，主要用在随机函数前设置 CPU 生成随机数的种子，确保每次运行随机函数生成的结果都一样，方便下次复现实验结果。

torch.set_default_tensor_type() 的用法参考此处 ¹⁰，主要用来设置 pytorch 中默认的浮点类型。

读取数据集

import torch.utils.data as Data

batch_size = 10

# combine features and labels of dataset
dataset = Data.TensorDataset(features, labels)
print(type(dataset))
# <class 'torch.utils.data.dataset.TensorDataset'>
print(dataset.__len__())
# 1000

# put dataset into DataLoader
data_iter = Data.DataLoader(
    dataset=dataset,            # torch TensorDataset format
    batch_size=batch_size,      # mini batch size
    shuffle=True,               # whether shuffle the data or not
    num_workers=4,              # read data in multithreading
)
print(type(data_iter))
# <class 'torch.utils.data.dataloader.DataLoader'>
print(data_iter.batch_size)
# 10

if __name__ == '__main__':
    for x, y in data_iter:
        print(x, '\n', y)
        # tensor([[0.0191, 1.6940],
        #         [-0.7821, -1.4237],
        #         [-1.3451, -0.9675],
        #         [2.0441, -1.3229],
        #         [0.2044, 0.1639],
        #         [0.2546, -0.5020],
        #         [-1.2512, -0.2749],
        #         [-0.2890, 0.1522],
        #         [0.1878, 0.2935],
        #         [0.0353, -0.3365]])
        # tensor([-1.5019, 7.4767, 4.7906, 12.7802, 4.0670, 6.4010, 2.6281, 3.1145,
        #         3.5805, 5.4059])
        
        print(x.shape, y.shape)
        # torch.Size([10, 2])
        # torch.Size([10])
        
        break

Data.DataLoader 的用法可以参考这里 ¹¹’ ¹²’ ¹³。

定义模型

from torch import nn

class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()           # call father function to init
        self.linear = nn.Linear(n_feature, 1)       # function prototype: `torch.nn.Linear(in_features, out_features, bias=True)`

    def forward(self, x):
        y = self.linear(x)
        return y

net = LinearNet(num_inputs)

# ways to init a multilayer network

# method Nr.1
net = nn.Sequential(
    nn.Linear(num_inputs, 1)
    # other layers can be added here
)

# method Nr.2
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......

# method Nr.3
from collections import OrderedDict
net = nn.Sequential(
    OrderedDict([
        ('linear', nn.Linear(num_inputs, 1))
    # ......
])
)

初始化模型参数

from torch.nn import init

init.normal_(net[0].weight, mean=0.0, std=0.01)
init.constant_(net[0].bias, val=0.0)  # or you can use `net[0].bias.data.fill_(0)` to modify it directly

for param in net.parameters():
    print(param)
# Parameter
# containing:
# tensor([[0.0044, -0.0017]], requires_grad=True)
#
# Parameter
# containing:
# tensor([0.], requires_grad=True)

定义损失函数

loss = nn.MSELoss()  					   # nn built-in squared loss function
										   # function prototype: `torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')`

print(loss)
# MSELoss()

print(type(loss))
# <class 'torch.nn.modules.loss.MSELoss'>

定义优化函数

import torch.optim as optim

optimizer = optim.SGD(net.parameters(), lr=0.03)  # built-in random gradient descent function
                                                  # function prototype: `torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)`
print(optimizer)
# SGD(
#     Parameter
# Group
# 0
# dampening: 0
# differentiable: False
# foreach: None
# lr: 0.03
# maximize: False
# momentum: 0
# nesterov: False
# weight_decay: 0
# )

print(type(optimizer))
# <class 'torch.optim.sgd.SGD'>

训练

num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        output = net(X)
        l = loss(output, y.view(-1, 1))
        optimizer.zero_grad()                   # reset gradient, equal to net.zero_grad()
        l.backward()
        optimizer.step()
    print('epoch %d, loss: %f' % (epoch, l.item()))
# epoch 1, loss: 0.000148
# epoch 2, loss: 0.000210
# epoch 3, loss: 0.000216

先后进行三次训练，得到每次的样本误差。

然后对用于生成数据集的 weight 和 bias 和经过训练计算而得到的 weight 和 bias 进行对比，如下所示：

# result comparision
dense = net[0]
print(f"weight:\n{true_w} V.S {dense.weight.data}")
print(f"bias:\n{true_b} V.S {dense.bias.data}")
# weight:
# [2, -3.4] V.S tensor([[ 1.9996, -3.3998]])
# bias:
# 4.2 V.S tensor([4.2004])

---

多层感知机

参考这里 ¹⁴

---

参考链接

---

1. 从零开始学Pytorch ↩︎

2. 从零开始学Pytorch（一）之常见数据操作 ↩︎

3. PyTorch中文文档 ↩︎

4. pytorch中的广播机制 ↩︎

5. Pytorch中的广播机制 ↩︎

6. 从零开始学Pytorch（二）之线性回归 ↩︎

7. Pytorch中requires_grad_(), detach(), torch.no_grad()的区别 ↩︎

8. TORCH.TENSOR.REQUIRES_GRAD_ ↩︎

9. 【pytorch】torch.manual_seed()用法详解 ↩︎

10. pytorch每日一学8(torch.set_default_tensor_type(t)) ↩︎

11. RuntimeError: DataLoader worker (pid(s) 9528, 8320) exited unexpectedly ↩︎

12. RuntimeError: DataLoader worker exited unexpectedly ↩︎

13. pytorch-Dataloader多进程使用出错 ↩︎

14. 从零开始学Pytorch（三）之多层感知机的实现 ↩︎