定义
总时差(总浮动时间)(TF,Total Free Time,不耽误项目总进度)=LS(Latest Start)-ES(Earliest Start)=LF(Latest Finish)-EF(Earliest Finish)。
自由时差(FF,Float Free Time,不耽误紧后工作的进度)=紧后工作ES-本工作的EF。对于无紧后工作的工作,其自由时差=工期-本工作的EF。
Introduction
看到这俩名词一开始会有点蒙,引入它们是为了解决一个什么问题呢?现在假设你是一个项目经理,有个项目涉及了ABCEDFGHI共九个工作模块,各个模块所需要的时间及制约关系在下图也标注了出来:
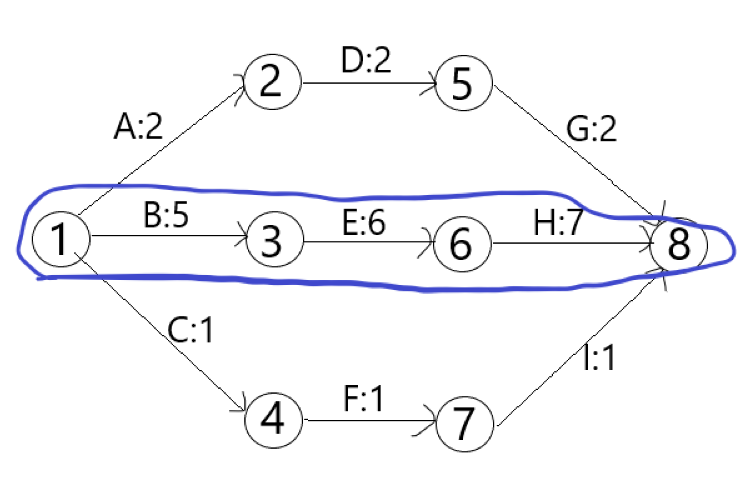
那么现在问题来了,你觉得这个项目最早完成时间是多少??很显然,蓝色画笔圈出来的也就是最长的那条路径上所有工作模块所需时间的总和就是最早完成时间,对吧?我们把这个时间呢,就称为工期,这条路径也就称之为关键路径。
还没完,接下来我要问你关键的问题了。这些模块中哪些模块可以晚点开始而不影响工期?能晚多久?哪些模块可以晚点开始而不影响其紧后结点呢?其实啊,这俩名词就是为了这俩问题而存在的。按照定义,你能不能把这九个工作模块他们的自由时差和总时差都算出来呢?
经过计算,你会发现,关键路径上的工作模块它们的总时差和自由时差均为0。这很好理解,毕竟关键路径上的模块时间推迟直接影响工期,所以它们的总时差是0,并且它们的推迟直接导致后面的模块推迟,所以自由时差也为0。
ADG这三个模块的总时差均为12,AD自由时差均为0,G的自由时差为12。
CFI这三个模块的总时差均为15,CF的自由时差均为0,I的自由时差等于15。
Context
其实,无非就是一个有向无环图嘛。
我们做图的时候,是把圆圈结点当作一个活动的结束或是另一个活动的开始,连接线表示活动,箭头表示活动的制约关系。
求一个活动的总浮动时间,就是粗暴的把从开始结点到结束结点,所有经过这条线的链路找出来,取那个最长的链路时间T,然后用工期减去T。
求一个活动的自由时差,如下图所示。你需要把从开始结点并经过活动1的的最长链路找到,记它的时间是T1吧;把从开始结点并经过活动2的的最长链路找到,记时间T2;记时间T3;,,,求这些时间的最大值我记为TMax=max{T1,T2,T3}。
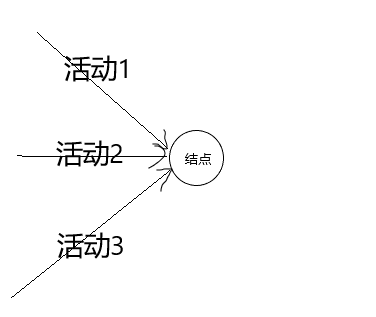
那么活动1的自由时差就等于TMax-T1;同理活动2,3,etc。
可以看出,如果本活动指向的结点并没有其它活动指向它的话,它的自由时差一定为0,因为就你自己个儿嘛,父母响应计划生育你能说啥。所以说自由它是一个相对的概念,没得其它活动在,或是你没得其它活动优秀,你就获得不了自由。
有的小伙伴可能要问了?自由时差的定义不是和紧后工作有关系吗?事实上,它们确实是 没有关系。你想啊,紧后工作的最早开始时间,可不就是之前所有链路的最长链路的时间嘛。
这也就意味着,。结点后面有一个活动或是多个活动,或是没有活动,都不对自由时差产生影响。特殊情况下,当结点为终结点时,此活动的自由时差的定义和总时差的定义是一样的。
就写到这里了,如果你愿意,可以用下面的练习题来加深理解:
Exercise
如下图,你能求出活动D的总时差与自由时差吗?
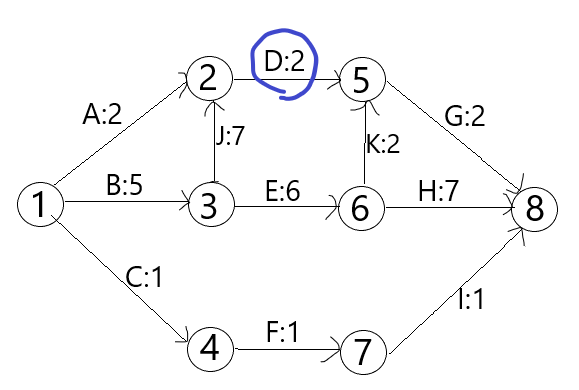
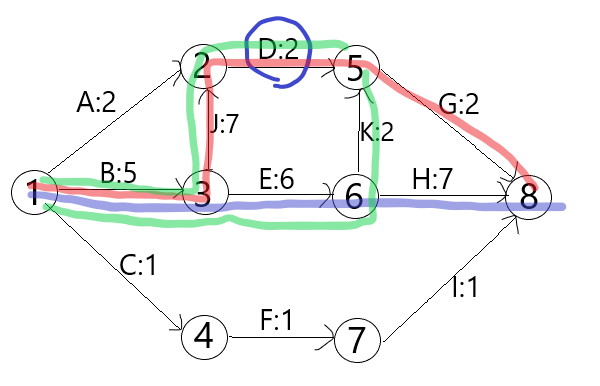
答案:D的总时差=2,自由时差=1.如下图,总时差是蓝色-红色;自由时差是两个绿色之差。
Summary
总时差和自由时差都是表示自由度的概念。
总时差是指不影响工期的前提下,本工作(也许是一个工作序列)可以利用的机动时间。;
自由时差是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
总时差总是大于等于自由时差的。
![English Learning - L2 第 3 次小组纠音 [ʌ] [ɒ] [ʊ] [ɪ] [ə] [e] 2023.3.4 周六](https://img-blog.csdnimg.cn/f15da8f7f9314c5ba02ec2c5dd42978b.png)


![[数据结构与算法(严蔚敏 C语言第二版)]第1章 绪论(学习复习笔记)](https://img-blog.csdnimg.cn/dd1bb8c16e3f4cc8908ea592ae7d3c8b.png)