Abstract&Introduction&Related Work
- 研究任务
用子网络做CL - 已有方法和相关工作
- 彩票假说(LTH)证明了稀疏子网络(称为中奖彩票)的存在,这些子网络保持了密集网络的性能,然而使用迭代修剪方法在持续学习过程中搜索最佳获胜门票需要对每个到达的任务进行重复剪枝和重新训练,这是不切实际的
- 基于剪枝的持续学习方法:
- CLNP使用 l 1 l_1 l1 正则化以诱导稀疏性并冻结它们以保持性能。之后,该模型重新初始化未被选择用于未来任务训练的神经元
- 在给定预训练模型的权重上训练任务特定的二进制掩码。该方法不允许在记忆每个任务的学习掩码时在任务之间进行知识转移,性能在很大程度上取决于主干模型的质量
- HAT提出了特定于任务的可学习注意力向量,以识别每个任务的重要权重,其中掩码用于在持续学习期间分层累积注意力向量
- LL-Tickets表明存在一个称为终身票的稀疏子网络,它在持续学习期间的所有任务中都表现良好。当获得的票不能在保持过去任务的性能的同时充分学习新任务时,该方法从当前票中搜索更突出的票。LL票据需要外部数据,以利用先前任务的学习模型最大化知识蒸馏,票扩展过程由另一系列重训练和剪枝步骤组成
- 面临挑战
- 创新思路
- 提出了 Winning Subnetworks(WSN)为每个任务学习一个紧凑的子网络,同时保持先前任务选择的权重不变。所提出的方法不执行任何用于学习子网络的显式修剪。这不仅可以消除灾难性遗忘,还可以将以前的任务学到的知识向前转移到新的任务
- 实验结论
WSN联合学习与每个任务相关联的子网络相关的模型权重和任务自适应二进制掩码,同时尝试通过重用之前子网络的权重来选择要激活的一小组权重(获胜票),每张中奖彩票产生的二进制掩码被编码为一个N位二进制数字掩码,然后使用霍夫曼编码进行压缩,以实现网络容量相对于任务数量的亚线性增长
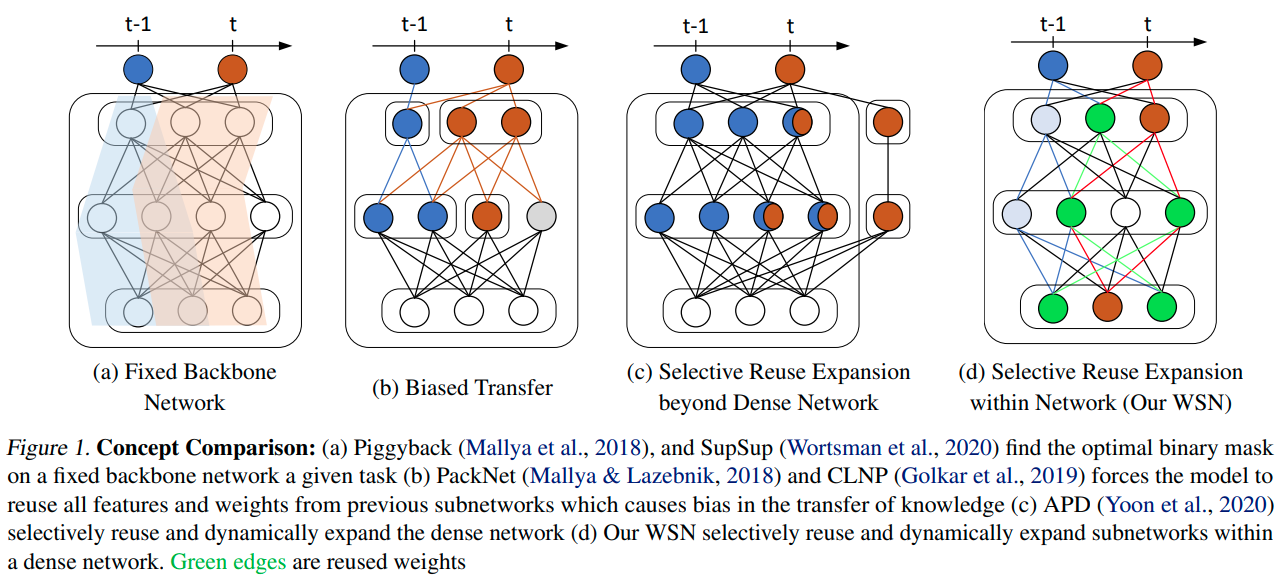
与图1a基于修剪的CL方法不同,该方法在预先训练的主干网络中获得特定于任务的子网络,我们逐步学习神经网络中的模型权重和任务自适应二进制掩码(子网络)。
为了在模型学习新任务时允许前向转移,我们将学习到的子网络权重重新用于先前任务,但有选择地,而不是使用所有权重(图1b),这可能会导致有偏的转移。
通过冻结先前任务的子网络权重,消除了持续学习过程中灾难性遗忘的威胁,并且不像
图1c 那样,不会受到负迁移的影响,图1c在训练新任务时可以更新先前任务的网络权重。权重的大小通常被用作查找彩票中使用的最佳子网络的修剪标准
然而在CL中,仅依赖权重大小可能是次优的,因为权重是跨类共享的,因此新任务的训练将改变先前任务训练的权重(重用权重)。这将触发雪崩效应,在学习器看来,选择作为后续任务子网络一部分的权重总是更好,这将导致先前任务知识的灾难性遗忘
在CL中,学习器在不改变重复使用的权重的情况下对新任务进行训练是很重要的。为了找到最优子网络,我们将学习参数和网络结构的信息解耦为两个独立的可学习参数,即权重和权重分数
权重分数是具有与权重相同形状的二进制掩码,通过选择权重排名得分最高的百分之k的权重,可以找到子网络
WSN在密集网络内选择性地重用和动态地扩展子网络,绿色边是重复使用的权重
Forget-Free Continual Learning with Winning SubNetworks
神经网络搜索任务自适应获胜票,并仅更新先前任务中未训练的权重。在对每个任务进行训练后,该模型冻结子网络参数,从而使所提出的方法不受设计的灾难性遗忘的影响
让每个权重都与一个可学习的参数相关联,称之为权重分数 s s s,它在数值上决定了与之相关的权重的重要性;也就是具有较高权重分数的权重被视为更重要。
我们找到神经网络的稀疏子网络 θ θ θ,因此它固有地减小了求解器的扩展的大小
图2是WSN如何在全网络中逐步获取二进制权重的过程,对权重的选择依赖于二进制的任务权重mask
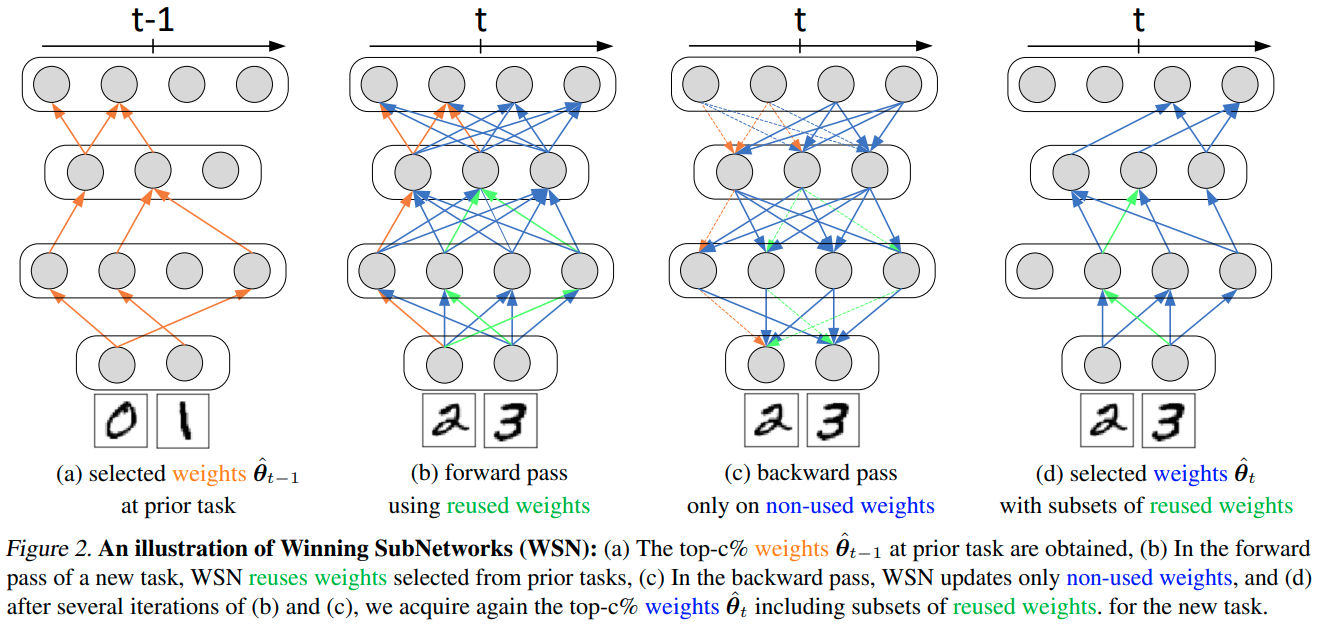
Optimization Procedure for Winning SubNetworks
为了共同学习与每个任务相关的子网络的模型权重和任务自适应二进制掩码,给定目标 L ( ⋅ ) L\left(\cdot\right) L(⋅),我们优化 θ θ θ 和 s s s,其中:
minimize θ , s L ( θ ⊙ m t ; D t ) \underset{\boldsymbol{\theta},\mathsf{s}}{\text{minimize}}\mathcal{L}(\boldsymbol{\theta}\odot\mathbf{m}_t;\mathcal{D}_t) θ,sminimizeL(θ⊙mt;Dt)
这种朴素优化程序存在两个问题:
- 当为新任务进行训练时更新所有 θ θ θ 会对分配给先前任务的权重造成干扰
- 指标函数总是具有0的梯度值;因此,用其损失梯度更新权重分数 s s s 是不可能的。为了解决第一个问题,通过只允许更新先前任务中未选择的权重来选择性地更新权重。为此使用累加二进制掩码 M t − 1 = ∨ i = 1 t − 1 m i \textbf{M}_{t-1}=\lor_{i=1}^{t-1}\textbf{m}_i Mt−1=∨i=1t−1mi 当学习任务t时,对于具有学习率 η η η 的优化器, θ θ θ 的更新公式为: θ ← θ − η ( ∂ L ∂ θ ⊙ ( 1 − M t − 1 ) ) \boldsymbol{\theta}\leftarrow\boldsymbol{\theta}-\eta\left(\dfrac{\partial\mathcal{L}}{\partial\boldsymbol{\theta}}\odot(\mathbf{1}-\mathbf{M}_{t-1})\right) θ←θ−η(∂θ∂L⊙(1−Mt−1))
有效地冻结为先前任务选择的子网络的权重。为了解决第二个问题,我们在反向传递中使用Straight-through Estimator,因为
m
t
m_t
mt 是通过前
c
c%
c 分数获得的,忽略指示函数的导数,并按如下方式更新权重得分:
s
←
s
−
η
(
∂
L
∂
s
)
\mathbf{s}\leftarrow\mathbf{s}-\eta\left(\dfrac{\partial\mathcal{L}}{\partial\mathbf{s}}\right)
s←s−η(∂s∂L)
使用单独的权重分数 s s s 作为选择子网络权重的基础,可以在解决当前任务 t t t 时重用先前选择的权重 θ ⊙ m t \boldsymbol{\theta}\odot\textbf{m}_t θ⊙mt 中的一些权重,这可以被视为转移学习
同不选择与新任务无关的先前选择的权重,而是从尚未选择的权重集合中选择权重以满足每个任务的目标网络容量,这可以被视为从任务 { 1 , . . . , t − 1 } \{1,...,t-1\}\quad\text{} {1,...,t−1} 到任务 t t t 的微调
伪代码:

Binary Mask Encoding
子网络需要一个二进制掩码来存储每个任务的任务特定权重,使用哈夫曼编码,网络容量相对于任务数量增长速度为亚线性
Experiments
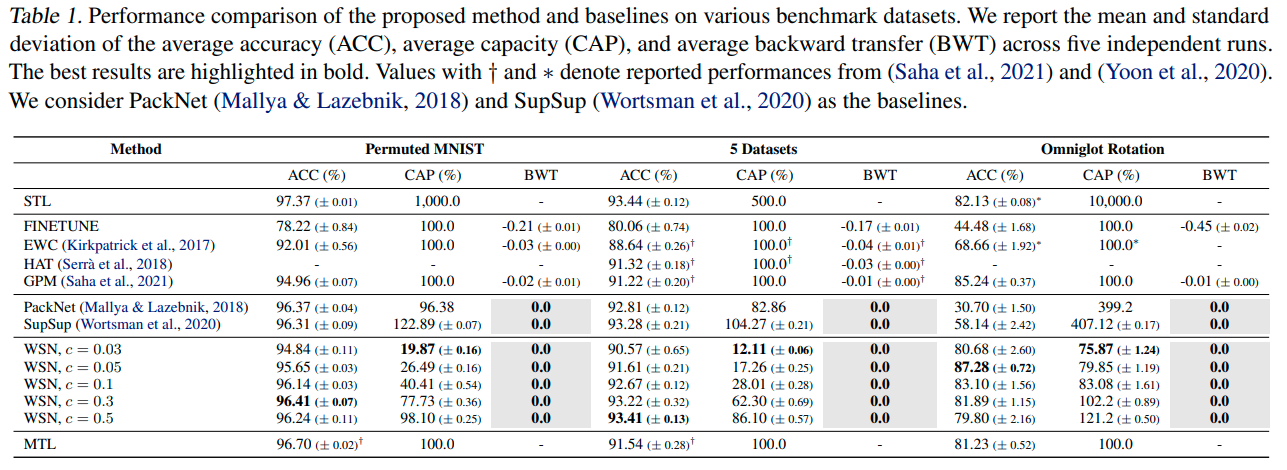
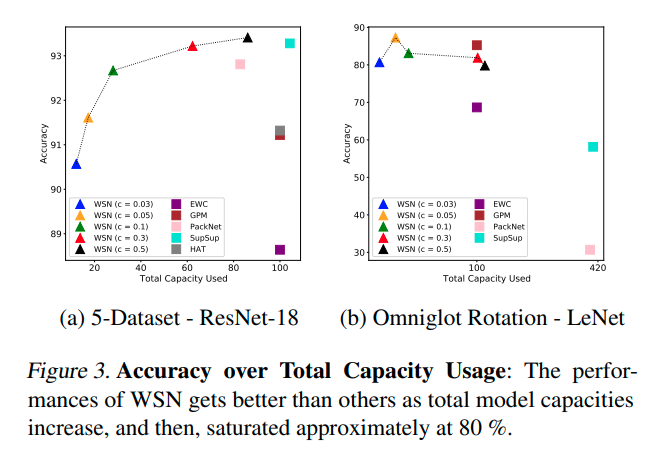
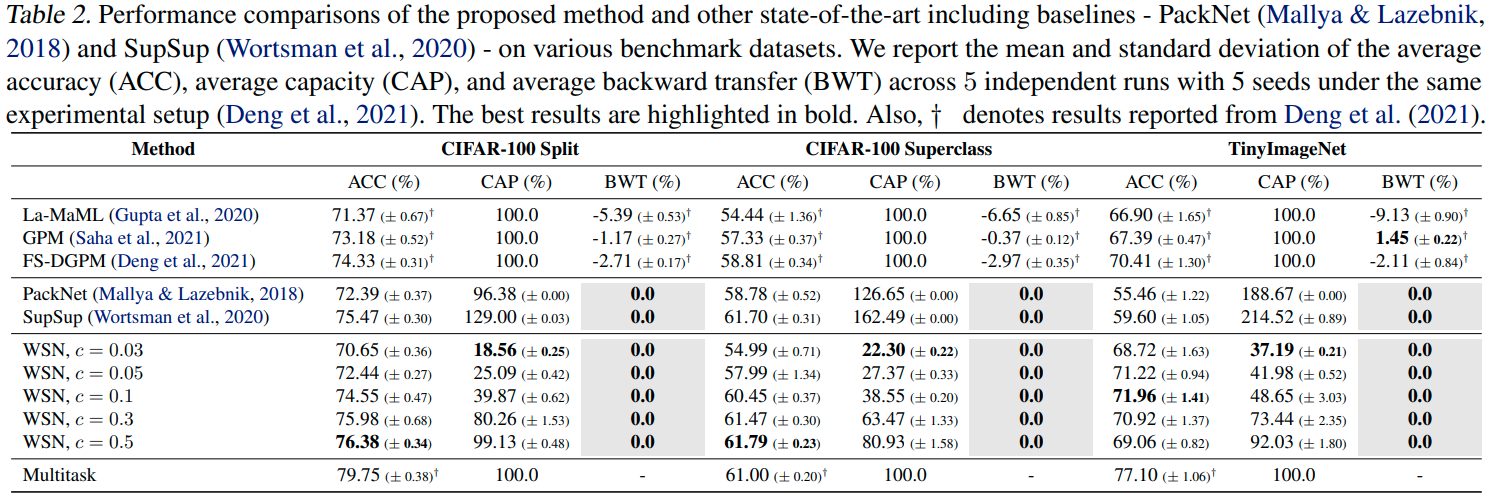
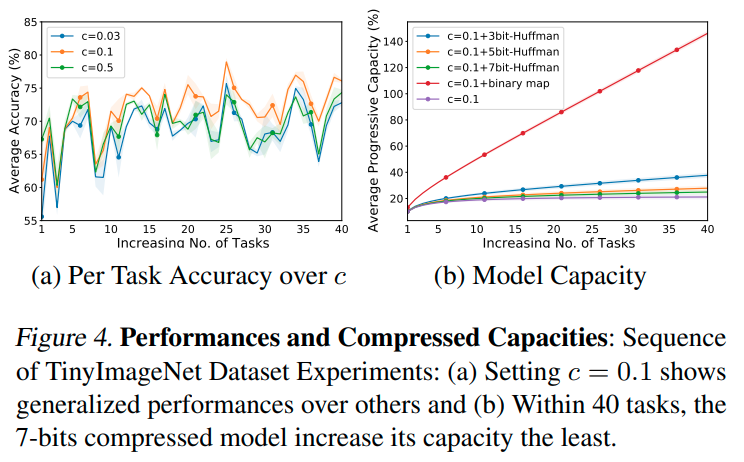
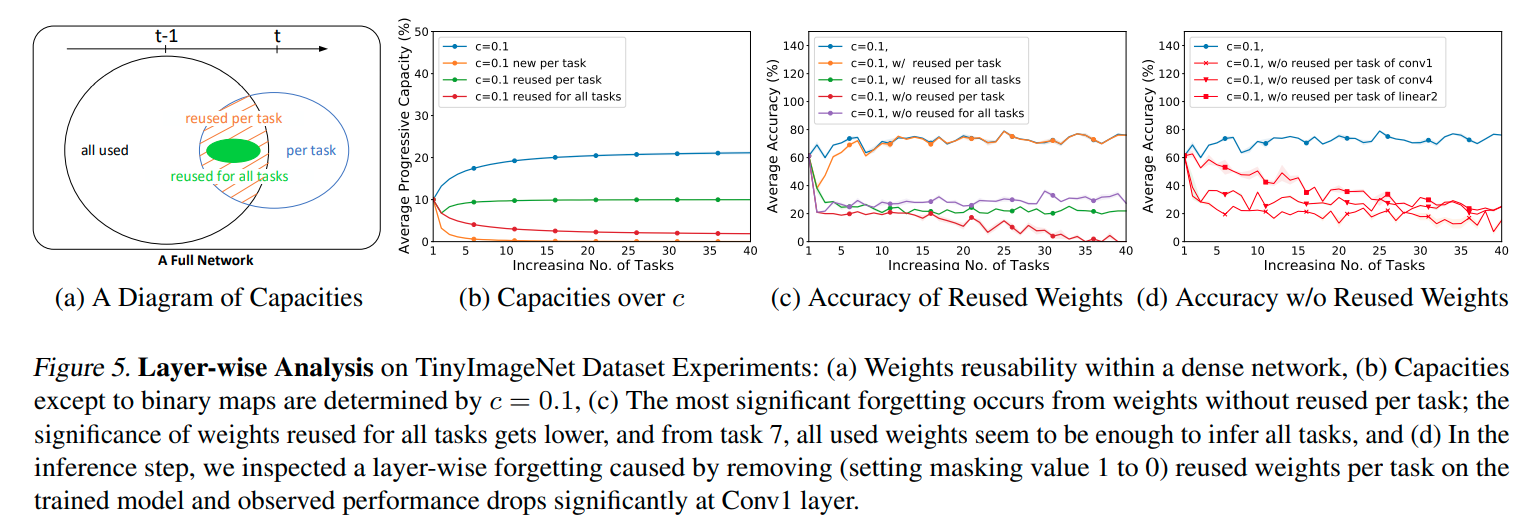
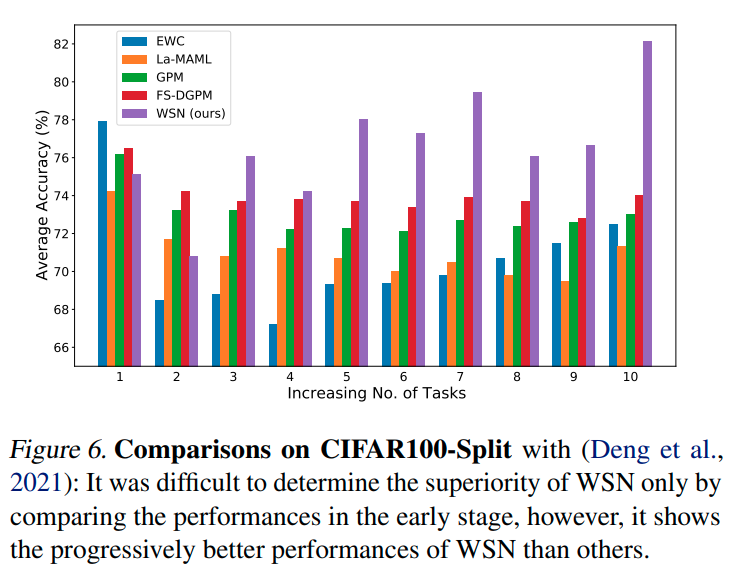
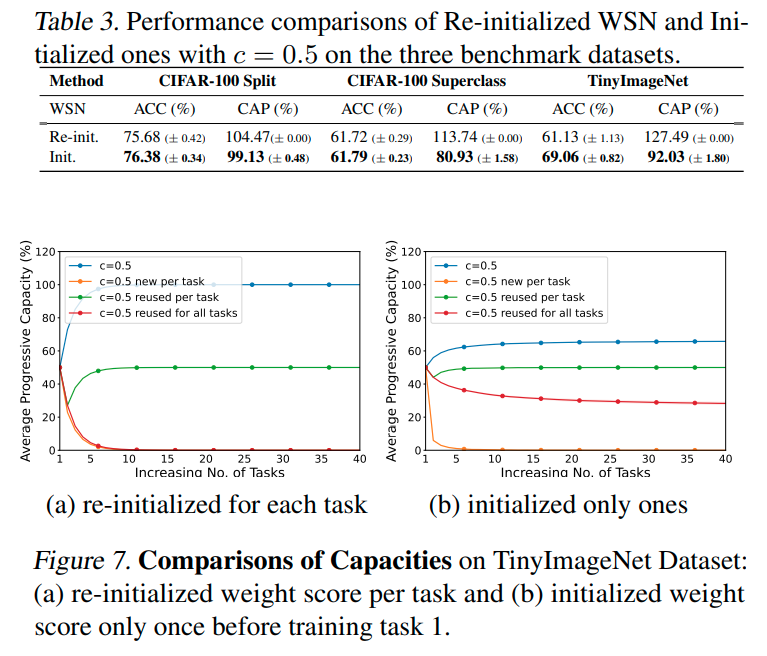
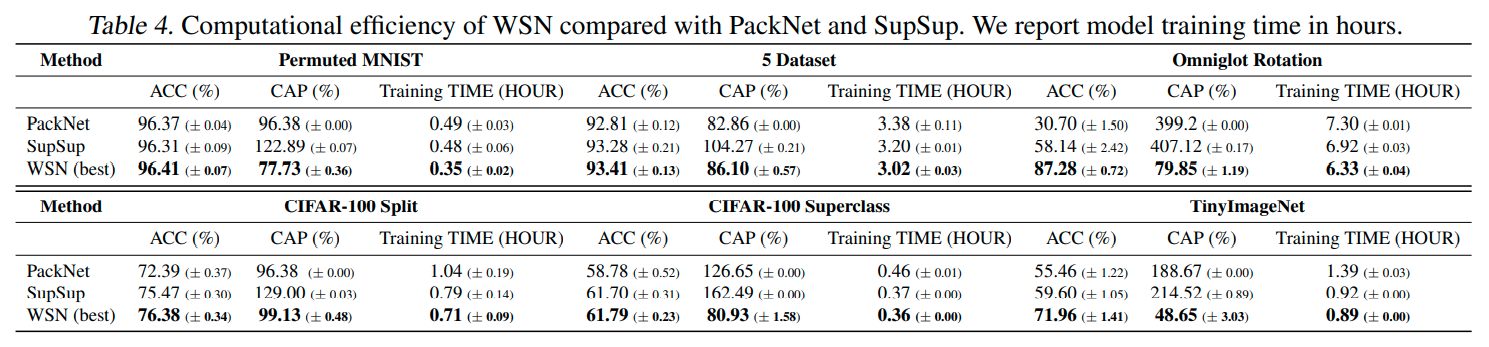
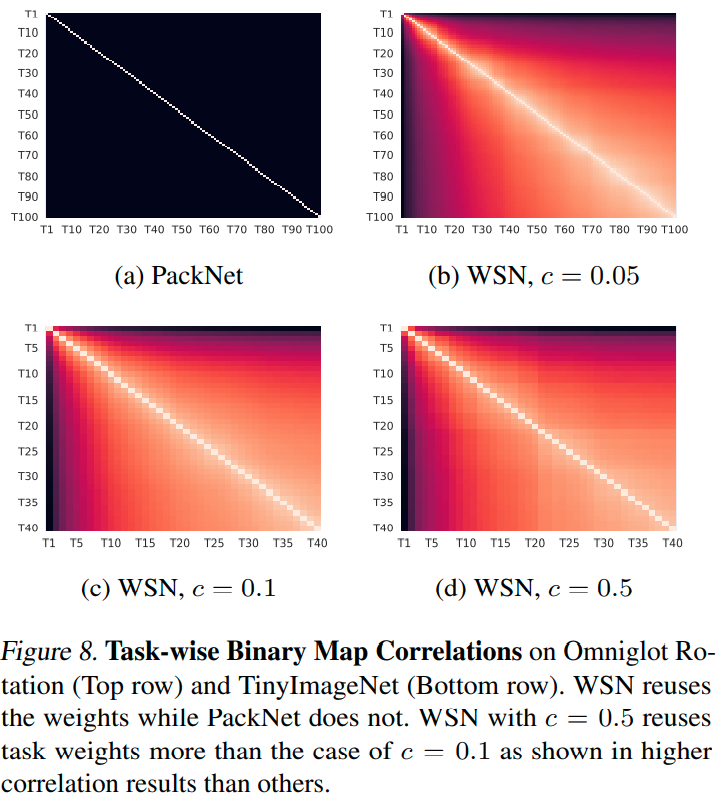
Conclusions
我们提出了一种受彩票假设启发的连续学习方法,该方法通过为每个任务找到最佳子网络来持续学习网络,假设子网络与密集网络一样工作良好。具体而言,在每次新任务到达时,我们使用单独的可学习权重分数来获得子网络,并存储子网络选择的二进制掩码,这允许为任何先前任务获得特定于任务的子网络。然后,我们使用先前任务的子网络的二进制掩码冻结子网络权重,并在新任务上训练子网络。这个过程消除了灾难性遗忘,并将知识从以前的任务转移到新的任务。我们在标准基准数据集上通过实验验证了我们的方法,在该数据集上,它为所有任务获得了一个紧凑的子网络,大大优于现有的连续学习方法,同时由于网络容量的对数增长,获得了小得多的网络-每个获胜票产生的二进制掩码被成功编码为一个N位二进制数字掩码,然后使用霍夫曼编码进行压缩,以实现任务数量的网络容量的亚线性增加
Remark
算是一种分布式?稀疏的思想 有点意思