1.5.1 全概率公式
在处理复杂事件的概率时，我们经常将这个复杂事件分解为若千个互不相容的较简单的事件之和，先求这些简单事件的概率，再利用有限可加性得到所求事件的概率,这种方法就是全概率公式的思想方法
全概率公式是概率论中的一个非常重要又实用的公式，它能使复杂事件的概率计算化繁就简，是计算复杂事件概率的有效方法。
定理 1.2设试验E 的样本空间为Ω,A1,A2，••••，An为E的一组事件，且满足：
(1)A1,A2,••••，An，两两互不相容,P(Ai)>0,i=1,2,••••,n;
(2)
Ai=Ω。
则对任一事件 B,有
P(B) =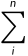 
P(A)P(BlA) (1.6)
式（1.6)称为全概率公式。称满足(1)和(2)的事件组 A1,A2,••••,An,为完备事件组或样本空间的一个划分．
证因为B=BΩ=B(Ai)=(BAi)由条件(1)BA1,…,BA2,••••,BAn,两两互不相容，根据有限可加性
P(B) =P(BAi)=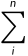P(BAi),
由假设P(Ai)>0（i=1,2,•••,n)及乘法公式得到
P(B)=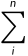P(BAi)= P(Ai)P(B|Ai)。
利用全概率公式求事件 B 的概率,关键是寻求完备事件组 A1,A2,•••，An，且
P（A,)和P（BIA,)为已知或容易求得,寻求完备事件组 Ai,Az，…，A，相当于找导
致事件B 发生的所有互不相容的事件.
【例 1.18】 假设有3箱同种型号零件,里面分别装有50件、30件、40件，而且
等品分别有20件、12 件和 24 件，现在任取一箱，再从所取的一箱中任取一个零件，
试求取出的零件是一等品的概率
1.5.2贝叶斯公式
在例 1.18 中,如果问题变为：已知取出的零件是一等品，问该零件来自第一箱的
概率多大？
这类问题是已知某事件(结果)已经发生，寻找导致该事件(结果〉发生的某种原
因的条件概率，解决这类问题的有效方法就是下面的贝叶斯公式•
定理 1.3 设试验E的样本空间为Ω,B为E的事件,A1,,A2，An事件组，且P（B≥0,P<A,2≥0.1=1,2，n,则
，…，A，为完备事
PA. B)
P(A)P(BA)
)'P(A, )P (B|A;)
=1,2,--.,n,
(1.7)
式（1.7)称为贝叶斯公式
容易看出，将全概率公式（1.6）代人条件概率公式P（A: BP(A)P(B A.)P(B)
，{一1,2,•，1 就得到了贝叶斯公式 (1.7).
【例1.19】 在例1.18 中,若已知取出的零件是一等品,问该零件来自这三箱的概率分别有多大？
解设A,=“任取的一箱为第之箱零件”,i=1,2,3,B一“取到的是一等品”
由例 1.18知PLA,: PIA, ) : PA) = =
P(A,) = P(A2) = P(A,) = 5. P(B|A,)
=0.4,
由贝叶斯公式得
12
P(B| A,)
=0.4,
30
P(B | Ag)
24
40
=0.6,
7
P(B):
15°
PLAIB)
PEB|AI)= DIAN)
1
P(A, |B) =
P(A,)P(B A,)
P(B)
x 0.4
3
7
15
1
P(A2|B) =
P(A2)P(B A2)
X 0.4
3
P(B)
7
15
P(A,|B) =
P(A, )P(B|A,)
P(B)
3 × 0.6
7
3
7
15,
例 1.20
9支手枪中有5支己校准过,4支末校准.—名射手用校谁过的枪射击时,命中率为 0.9，用未校准过的枪射击时，命中率为 0.3,现从这？支枪中任取一支=射击.
(1）求他能命中日标的概率;《2）如果他命中目标，求所用的枪是校准过的概率
解：
(1）设B={命中目标}，A,={所用的枪校准过}，A，一{所用的枪未校
准〉，则
P(A,) =5/9,
P(A,) =4/9,
P(B| A) =0.9, P(B A2) =0.3
442
由全概率公式，有
P(B) = SPCA) P(B | A,) =8/0 X0.0 + 4/0 X0.3 = 19/30.
(2）由贝叶斯公式，有
AL A
P(B| A,)P(A,)
0.9 X 5/9
15
P(A, | B)
P(B)
19/30
199. 1.乙7
【例 1.21】 玻璃杯成箱出售，每箱20 只,假设各箱含 0,1,2 只残次品的概率分别是 0.8,0.1和0.1某顾客欲购一箱玻璃杯，在购买时，售货员随机取出一箱，顾客开箱随机地查看四只,若无残次品，则买下该箱玻璃杯，否则退回，试求：
(1)顾客买下该箱玻璃杯的概率a；
(2)在顾客买下的一箱中,确实没有残次品的概率 B.
解:
设B=“顾客买下该箱玻璃杯”，A;=“抽到的一箱中有之件残次
品”,i=0,1,2.
(1)事件B 在下面三种情况下均会发生：抽到的一箱中没有残次品、有1件残次
品或有2件残次品•显然Ao,Ai,A， 是完备事件组.由题意知
P(A,) =0.8, P(A,) =0.1, P(A2) =0.1,
P(B A)
Cèo
=1, P(B A,)
C'o
Cio
Cèo
4
5'
P(B A2)
CH
C'o
12
19'
由全概率公式得
a =P (B) = P (A )P (B|A.) + P (A,)P (B A,) + P (A2 )P (B A 2) =0.94.
(2）由贝叶斯公式，有
P (A.)P (B Ao)
ß= P(A, B)
P(B)
0 8 X1
=0.85.
注意，在使用贝叶斯公式时，如果A和A是
一个完备事件组,事件B 为试验区
的任一事件，P(B)＞0.则贝叶斯公式的一种常用简单形式为
P(AB)
=
P(AP(BA)
PCAPCBA+PCAPCBIA)
#9袋
【例1.222 根据以往的记录，某种诊断肝炎的试验有如下效果：对肝炎患者的试验呈阳性的概率为 0.95;非肝炎患者的试验呈阴性的概率为 0.95.对自然人群进行普查的结果为：有千分之五的人惠有肝炎.现有某人做此试验结果为阳性，问此人确有
肝炎的概率为多少？
解设A=“某人确有肝炎”，B =“某人做此试验结果为阳性”．由己知条件有
P(B A)=0.95，
P（BIA=0.95,PCA）=0.005，
从而
P(A)=1- P(A) =0.995,
P(BIA) =1-P(B A) =0.05.
由贝叶斯公式，有
PA)P BA)
0.005 X 0.95
P(AB) =
=
= 0.087
P(A)P(B A) +P(A)PB A)
0.005 X 0.95 + 0.995 X 0.05
本题的结果表明，虽然P(B④)=0.95,P（B1④）=0.95,这两个概率都很高，但
是P（A 1B)=0.087，即试验阳性的人有肝炎的概率只有 8.7%.如果不注意这一点，
将P(BlA)和PCAIB)搞混，将会得出错误诊断，造成不良的后果
在贝叶斯公式中，事件 A： 的概率P（A.),i=1,2,…,n,通常是人们在试验之前
对 A， 的认知,习惯上称其为先验概率•若试验后事件B 发生了，在这种信息下考察
A，的概率P（A. 1B),i=1,2,⋯，n，它反映了导致B发生的各种原因的可能性大
小,常称为后验概率.
贝叶斯公式是英国数学家贝叶斯(Thomas Bayes,英,1701—1761）在其著作《机
会问题的解法》中首先提出的，该著作于 1763 年发表．经过多年的发展和完善,贝叶
斯公式的思想已经发展成为一整套统计推断方法，即“Bayes 方法”,这一方法在计算
机诊断、模式识别、基因组成、蛋白质结构、经济分析等很多方面都有应用.
