1.4.1 条件概率
在实际问题中,除了直接考虑某事件 B 发生的概率P(B)外,有时还会碰到这样的问题,就是“在事件A 已经发生的条件下,事件B 发生的概率”。一般情况下,后概率与前一概率不同,为了区别,我们常把后者称为条件概率,记为P(BIA),读作事件A 发生条件下事件B 发生的条件概率。 先看一个例子。
【例1.13】 某厂的100件产品中有5件是不合格品,而5件不合格品中有3件次品,2件废品.现从100 件产品中任意抽取一件,假定每件产品被抽到的可能性都相同,求
(1)抽到次品的概率;
(2)在抽到的产品是不合格品的条件下,产品是次品的概率
题解:
例 1.13 条件概率类型一——某工厂次品率
定义1.6 设A 与B是同一样本空间中的两个事件,若P(A)>0,则称
P(B|A)=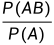 =
=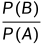 =
=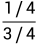
为在事件 A 发生下的事件 B 发生的条件概率
不难验证,条件概率P(•IA)满足概率定义1.5中的三条公理:
(1)非负性:对任意事件 B,P(BIA)≥0
(2)规范性:P(RIA)=1;
(3)可列可加性:设事件B1,B2,…B3,Bn,…两两互不相容,则P(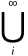 Bi|A)=
Bi|A)=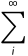 P(Bi|A).
P(Bi|A).
所以,条件概率P(•lA)也满足概率的其他所有性质.
【例 1.14】 某家庭中有两个孩子,己知其中至少有一个是男孩,求两个都是男孩
的概率(假设男、女孩出生率相同).
解用g代表女孩,6代表男孩,A 一“该家庭中至少有一个男孩”,B
一“两个
都是男孩”,本题求的是条件概率P(BIA).该家庭两个孩子的情况无非是 66,bg
§6,g§四种情况之一,即2=166,bg,gb,gg),B一^66),A={66,6g,g6〉,所以有
1
P(A) =
3 , P (B) =
4
4
,故
P(AB)
P(B A)=
P(A)
P(B)
P(A
1/4
=1/3.
3/4
注在事件 A 发生条件下,该家庭两个孩子的情況只能是 66,bg,g6三种情况
之一,即此时样本空间缩小为 2一{66,6g,g6)=A,B={66),所以根据古典概型有
P(BIA)=
-这种解法称为求条件概率的缩小样本空问法.
【例 1.15】 设某种动物以出生起活 20 岁以上的概率为 80%,活25 岁以上的概
率为 40%.如果现在有一个 20岁的这种动物,求它能活25 岁以上的概率
解 设事件 A一“该种动物能活 20 岁以上”,事件B一“该种动物能活 25岁以
上”,按题意,P(A)=0.8,由于BCA,所以P(AB)=P(B)=0.4.由条件概率定义
P(B A)
P(AB)
P(A)
0.4
= 0.5.
0.8
1,但
1.4.2 乘法公式
由条件概率公式容易得到下面定理.
定理 11设1 与B是同一样本空间中的两个事件,如果P(A)二0,则P(AB) =P(A)P(BlA).
(1.3
如果P(B)二0,则
PC4B)=PBPCAIB).
上面式(1.3),式(1.4)均称为事件概率的乘法公式
定理1.1容易推广到任意有限多个事件积事件概率的情况.
例如,若卩(A,Az•A,=1)二0,则
P(A,A,.A,)=PCAPCA,IA PCAs IA A2-PCA, IA,Az•A,-1.
(1.4
(1.5)
事实上,因为
PA,)≥P(A, AD >PCA,A,A,二…≥PCA Az•A13 ≥0,
所以式(1.5)中各条件概率均有意义,由条件概率定义,得
P(A,)PCA, IA,PCA, IAIA2.PCA, IA,A2.An-1
= P(A.) .
P(A,4.)
PCA:A:A,)
PCA,)
••
P(A A •An)
P (A,A,)
PCA,A2.•A,-1)
-PCA A•A,).
【例1.16】 某人忘记了电话号码的最后一位数字,因而他随意地拨号•求他拔号
不超过三次而接通电话的概率.
解设A,一“第之次接通电话”,i=1,2,3,B一“拨号不超过了次接通电话”,则
B=AI U A,A, U A A.As.
利用概率的有限可加性和乘法公式,有
P(B)=PCA,)+PCAIAD +P(A,A,A.)
= P(A;) + P (A) P (A2 l A,) + P(A,)P (A2 | A,)P (A, | A, A,)
1
10*
9
10 t.
9
+ %x.
1
= X
3
8
10*
【例 1.17】 猎手在距猎物 10 米处开枪,击中的概率为0.6.若击不中,待开第
枪时猜物已逃至30米远处,此时击中的概率为 0.25,若再击不中,则猎物已逃至 50
米远处,此时只有0.1的击中概率.求猎手三枪内击中猎物的概率
解以A,=“第之枪击中猎物”,i=1,2,3,则所求概率为 PCA UA,UA..
P(A, U A2 U A.) = 1 - P(A, UA, U A.) =1 - P(A, A, A .)
=1 - P(A,) P(A. | A,)P (A, | A, A,)
=1 - [1 - P (A,)J1 - P (A2 | A,)I[1 - P(A, | A, A ,)]
=1 - (1 - 0.6) (1 - 0.25) (1
=01)
=0.73.











![[算法]选择排序](https://img-blog.csdnimg.cn/8d8a9e9a817442f4b9717b3e950bc90f.png)