格的基本定义

定义1 给定$n$维实数空间${\mathbb{R}}^n$中的一组线性无关向量 B = { b 1 , … , b n } ⊂ R n \bm{B} = \{ \bm{b}_1, \dots, \bm{b}_n \} \subset \mathbb{R}^n B={b1​,…,bn​}⊂Rn，其整数系数线性组合构成的集合被称为格（Lattice），即 L = ∑ i = 1 n b i ⋅ Z = { B x : x ∈ Z n } \mathcal{L} = \sum^n_{i=1} \bm{b}_i \cdot \mathbb{Z} = \{ \bm{B} \bm{x} : \bm{x} \in \mathbb{Z}^n \} L=∑i=1n​bi​⋅Z={Bx:x∈Zn}。

定义中，冒号$:$有时也写成竖号$|$，表示满足（subject to，s.t.）的意思； B = { b 1 , … b n } \bm{B} = \{ \bm{b}_1, \dots \bm{b}_n \} B={b1​,…bn​}被称为格基。

如下图所示，同一个格$\mathcal{L}$可能有不同格基，如 B = { b 1 , … , b n } \bm{B} = \{ \bm{b}_1, \dots, \bm{b}_n \} B={b1​,…,bn​}或 C = { c 1 , … , c n } \bm{C} = \{ \bm{c}_1, \dots, \bm{c}_n \} C={c1​,…,cn​}，即$\mathcal{L}={\sum }_{i=1}^n{\mathbf{b}}_i\cdot \mathbb{Z}={\sum }_{i=1}^n\cdot \mathbb{Z}$。

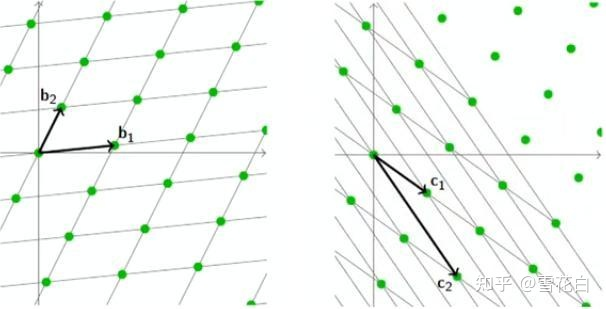
为了区分格基以方便阅读，有时会特地注明$\mathcal{L}(\mathbf{B})$或$\mathcal{L}(\mathbf{C})$。

对${\mathbf{b}}_1,\dots ,\mathbf{n}\in {\mathbb{R}}^m$，若$m=n$，则$\mathcal{L}=\mathcal{L}(\mathbf{B})$被称为满秩格。在格密码中，一般研究的是满秩格。

也可以不用基向量表示格，而把格看成欧式空间上点集的离散子群。群这个概念在现代密码学中很重要。很多密码方案的设计都涉及到群这个工具。从这个角度出发，可以更好地把握格密码学习的切入点。

定义2 格（Lattice）是${\mathbb{R}}^n$的满足离散性质的加法子群。

群的完整定义具体可以参考Introduction to Modern Cryptography这本书，这本经典教材有一门公开课。

密码学原理《Introduction to modern Cryptography》_哔哩哔哩_bilibili

简而言之，群是一个集合，在该集合上有一种二元运算，二元运算满足封闭性和结合律、且存在单位元和逆元，若再满足交换律则称为阿尔贝群。易证${\mathbb{R}}^n$是加法群，$\mathcal{L}$是${\mathbb{R}}^n$的子群而且是离散的。

格的基本区域

定义3 对格基 B = { b 1 , … b n } \bm{B} = \{ \bm{b}_1, \dots \bm{b}_n \} B={b1​,…bn​}，所有在$[0,1{)}^n$中的实数系数组合生成的空间称为格的基本区域，即$\mathcal{P}(\mathbf{B})={\sum }_i{\mathbf{b}}_i\cdot [0,1)$或 P ( B ) = { B ⋅ a ∣ a ∈ R n , 0 ≤ a i ≤ 1 } \mathcal{P}(\bm{B}) = \{ \bm{B} \cdot \bm{a} | \bm{a} \in \mathbb{R}^n, 0 \leq a_i \leq 1 \} P(B)={B⋅a∣a∈Rn,0≤ai​≤1}。

格的基本区域算是一个基本量。

这个定义中的公式有点难以理解。以图2为例，假如$\mathbf{a}=(0.2,0.33)$，则可得到蓝色向量；取$\mathbf{a}$的所有可能值，可获得所有可能的蓝色向量，所有可能的蓝色向量叠加起来构成的区域即格的基本区域。

换个说法，所有基向量张成的平行多面体即格的基本区域。平行多面体有点类似机器学习里的超平面，超过三维时难以想象它长什么样子。平行多面体里的“平行”指的是几何体的每个面都有与之相对平行的一个面。

定理1 假设格$\mathcal{L}$的秩为$n$，对$\mathcal{L}$上的一组线性无关向量 B = { b 1 , … , b n } \bm{B} = \{ \bm{b}_1, \dots, \bm{b}_n \} B={b1​,…,bn​}，当且仅当 P ( B ) ∩ L = { 0 } \mathcal{P}(\bm{B}) \cap \mathcal{L} = \{ \bm{0} \} P(B)∩L={0}时，$\mathbf{B}$是$\mathcal{L}$的格基。该定理被称为格基判定定理。

证明： 分为两步走，首先证明必要性，再证明充分性。
（1）必要性：当$\mathbf{B}$是$\mathcal{L}$的格基时， P ( B ) ∩ L = { 0 } \mathcal{P}(\bm{B}) \cap \mathcal{L} = \{ \bm{0} \} P(B)∩L={0}。
$\mathcal{L}$的格点由$\mathbf{B}$的整数系数组合形成，而$\mathcal{P}(\mathbf{B})$则由$\mathbf{B}$的小于1的实数系数组合形成，易知两者交集仅有原点$0$。
（2）充分性：当 P ( B ) ∩ L = { 0 } \mathcal{P}(\bm{B}) \cap \mathcal{L} = \{ \bm{0} \} P(B)∩L={0}时，$\mathbf{B}$是$\mathcal{L}$的格基。
由于$\mathbf{B}$在$\mathcal{L}$上，故存在$\mathbf{r}\in {\mathbb{R}}^n$使得$\sum {\mathbf{b}}_i\cdot r_i$也在格上。以下图为例，选取的$\mathbf{r}$可以是$(0.5,0.5)$。

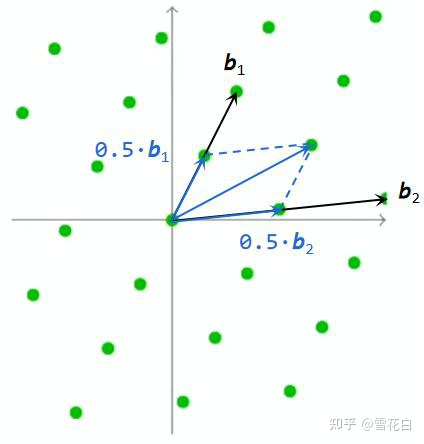
此外，由于$\mathbf{B}$在$\mathcal{L}$上，$\mathbf{B}$是某组格基乘以对应的整数系数向量，故$\sum {\mathbf{b}}_i\cdot \lfloor r_i\rfloor$也在格上。此处$\lfloor \cdot \rfloor$是向下取整符号。由格的二元运算封闭性可得，$\sum {\mathbf{b}}_i\cdot (r_i-\lfloor r_i\rfloor )$也在格上。

由于$0\le r_i-\lfloor r_i\rfloor <1$，故$\sum {\mathbf{b}}_i\cdot (r_i-\lfloor r_i\rfloor )$在$\mathcal{P}(\mathbf{B})$中。

综上，$\sum {\mathbf{b}}_i\cdot (r_i-\lfloor r_i\rfloor )$是$\mathcal{L}$和$\mathcal{P}(\mathbf{B})$的交集点。由于 P ( B ) ∩ L = { 0 } \mathcal{P}(\bm{B}) \cap \mathcal{L} = \{ \bm{0} \} P(B)∩L={0}，可得$r_i=\lfloor r_i\rfloor$，即它必然是整数。

证毕。

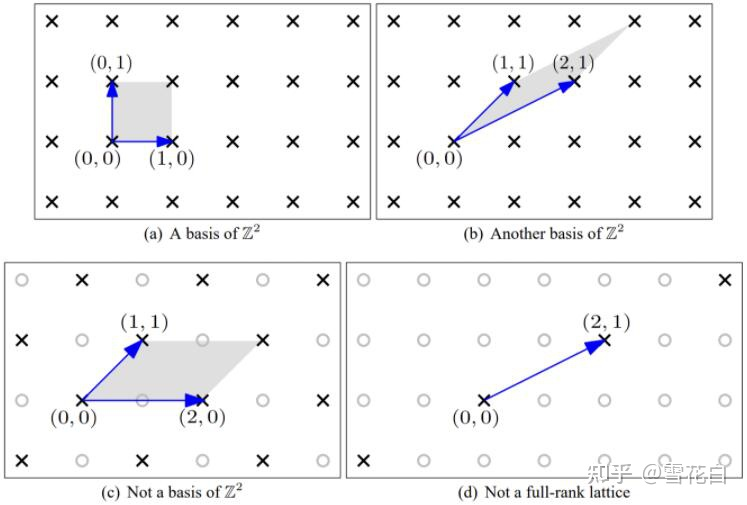
用定理1可以判断一组线性无关向量是否为格基，以下图为例。对于格${\mathbb{Z}}^2$，图(a)和图(b)都是格基，而图©由于$\mathcal{P}(\mathbf{B})$包含非零格点$(1,0)$故不是格基，图(d)由于$\mathcal{P}(\mathbf{B})$不包含格点$(0,0)$故也不是格基。

格的行列式

定义4 基本区域$\mathcal{P}$的体积称为格的行列式，即$\det (\mathcal{L})=\mathrm{vol}(\mathcal{P})$。

体积这个词有点抽象，一维空间里指长度，二维空间里指面积，三维及以上等多维空间里指体积。下文链接给出一个示例说明为何行列式就是体积。

Bat特白：行列式就是体积/面积？——（一）

不同的格基定义了不同的基本区域，然而所有基本区域的体积均一样。以下图为例，蓝色区域和黄色区域的体积是一样的。换而言之，对于$\mathcal{L}=\mathcal{L}(\mathbf{B})=\mathcal{L}(\mathbf{C})$，有$\mathrm{vol}(\mathcal{P}(\mathbf{B}))=\mathrm{vol}(\mathcal{P}(\mathbf{C}))$。

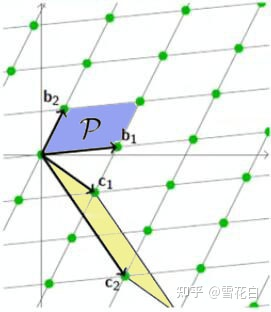
行列式不是某一组基向量的性质，而是格本身的性质，即格的不变量。为了证明这个关系，接下来先介绍矩阵相乘行列式和不同格基之间的关系。

矩阵相乘的物理意义是将一个坐标系中的点映射到另一个坐标系中去。假设存在两个矩阵${\mathbf{M}}_1$和${\mathbf{M}}_2$，有$\det ({\mathbf{M}}_1{\mathbf{M}}_2)=\det ({\mathbf{M}}_1)\det ({\mathbf{M}}_2)$。

怎么证明行列式乘法定理：|AB|=|A||B|?

简而言之，$\det ({\mathbf{M}}_2)$求出矩阵${\mathbf{M}}_2$包含多少个正交基基本区域，$\det ({\mathbf{M}}_1)$求出正交基基本区域经过${\mathbf{M}}_1$变换后的体积，二者相乘得到矩阵${\mathbf{M}}_1{\mathbf{M}}_2$的体积。

定理2 对于两组不同的格基$\mathbf{B}$和$\mathbf{C}$，当且仅当存在幺模矩阵$\mathbf{U}$使得$\mathbf{C}=\mathbf{UB}$时，$\mathbf{B}$和$\mathbf{C}$对应的格一样，即$\mathcal{L}(\mathbf{B})=\mathcal{L}(\mathbf{C})$。

证明： 分为两步走，先证明必要性，再证明充分性。
（1）必要性：若$\mathcal{L}(\mathbf{B})=\mathcal{L}(\mathbf{C})$，则$\mathbf{C}=\mathbf{UB}$且$\mathbf{U}$是幺模矩阵。

易知存在矩阵$\mathbf{U}$和$\mathbf{V}$使得$\mathbf{C}=\mathbf{UB}$和$\mathbf{B}=\mathbf{VC}$，有$\mathbf{C}=\mathbf{UVC}$，$\mathbf{UV}=\mathbf{I}$。

进一步有$\det (\mathbf{I})=\det (\mathbf{U})\det (\mathbf{V})=1$。

注意，由于$\mathbf{C}\in \mathcal{L}$是格基，它在格上，由定义1可知，$\mathbf{U}$是整数系数生成的矩阵；同理，$\mathbf{V}$也是整数矩阵。因此，有$\det (\mathbf{U})=\det (\mathbf{V})=\pm 1$，即$\mathbf{U}$和$\mathbf{V}$都是幺模矩阵。

（2）充分性：若$\mathbf{C}=\mathbf{UB}$且$\mathbf{U}$是幺模矩阵，则$\mathcal{L}(\mathbf{B})=\mathcal{L}(\mathbf{C})$。

注意幺模矩阵是整数矩阵，易知$\mathcal{L}(\mathbf{C})=\sum {\mathbf{c}}_i\cdot \mathbb{Z}=\sum b_j\cdot \mathbb{Z}\cdot \mathbb{Z}\subseteq \mathcal{L}(\mathbf{B})$；同理，有$\mathcal{L}(\mathbf{B})\subseteq \mathcal{L}(\mathbf{C})$。综上，有$\mathcal{L}(\mathbf{B})=\mathcal{L}(\mathbf{C})$。

证毕。

推论1 对于$\mathcal{L}=\mathcal{L}(\mathbf{B})=\mathcal{L}(\mathbf{C})$，有$\mathrm{vol}(\mathcal{P}(\mathbf{B}))=\mathrm{vol}(\mathcal{P}(\mathbf{C}))$。

证明： 根据定理2，有$\mathbf{C}=\mathbf{UB}$且$\mathbf{U}$是幺模矩阵，则$\det (\mathbf{C})=\det (\mathbf{UB})=\det (\mathbf{U})\det (\mathbf{B})=\pm \det (\mathbf{B})$，正负号表示方向，而体积取绝对值。

证毕。

定义5 记格基为 B = { b 1 , … , b n } \bm{B} = \{ \bm{b}_1, \dots, \bm{b}_n \} B={b1​,…,bn​}，中心平行多面体的定义为$\mathcal{P}={\sum }_{i=1}^n{\mathbf{b}}_i\cdot [-\frac{1}{2},\frac{1}{2})$。

如下图所示，当格的秩为2时，以原点为中心的橘红色区域即中心平行多面体。

与中心平行多面体平行的所有基本区域叠加起来可以张成整个空间，且构成空间的一种划分。即 { P + x ∣ x ∈ L } \{ \mathcal{P} + \bm{x} | \bm{x} \in \mathcal{L} \} {P+x∣x∈L}是${\mathbb{R}}^n$的一种划分方式，如图的灰色斜线是${\mathbb{R}}^n$的一种划分。

如果在欧式空间中任意取一个足够大的超球体$\mathbf{S}\subseteq {\mathbb{R}}^n$，可以发现球中基本平行多面体的个数与球的体积大致成线性关系，换而言之，球中格点的个数与球的体积近似成正比例，即$|\mathbf{S}\cap \mathcal{L}|\approx \mathrm{vol}(\mathbf{S})/\det (\mathcal{L})$。

从密度的角度来看，行列式只是根据空间中一块足够大的区域中格点的数量来定义，即$\det (\mathcal{L})\approx \mathrm{vol}(\mathbf{S})/|\mathbf{S}\cap \mathcal{L}|$，所以行列式不依赖于具体格基的取值。同样可“证”推论1。

一个单位球里格点的个数可以看成密度，两个不同格可能密度一样，但格点的位置排布大不相同。

致谢

• Simons格密码公开课官网

Mathematics of Lattices - Simons Institute for the Theory of Computing

• 哔哩哔哩中英双语视频（字幕组：重庆大学大数据与软件学院 后量子密码研究小组）

【中英字幕】Simons格密码讲座第1讲：格的数学定义_哔哩哔哩_bilibili

• 其它格密码讲解课程和博文

格密码入门课程_哔哩哔哩_bilibili

格密码的基础概念_唠嗑！的博客-CSDN博客_格密码

格（Lattice）基础（一）_Amire0x的博客-CSDN博客_两组格基生成同一个格的充要条件