题目描述
现有一棵
n个结点的二叉树(结点编号为从0到n-1,根结点为0号结点),求两个指定编号结点的最近公共祖先。
注:二叉树上两个结点A、B的最近公共祖先是指:二叉树上存在的一个结点P,使得P既是A的祖先,又是B的祖先,并且P需要离根结点尽可能远(即层号尽可能大)。
输入描述
第一行
3个整数n、k1、k2(1≤n≤50,0≤k1≤n−1,0≤k2≤n−1),分别表示二叉树的结点个数、需要求最近公共祖先的两个结点的编号;接下来
n行,每行一个结点,按顺序给出编号从0到n-1的结点的左子结点编号和右子结点编号,中间用空格隔开。如果不存在对应的子结点,那么用-1表示。
输出描述
输出一个整数,表示最近公共祖先的编号。
样例
输入
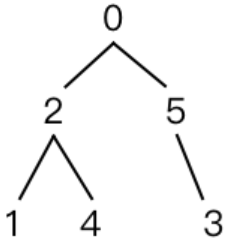
6 1 4 // 共有6个节点【编号0~5】,目标节点编号为1和4
2 5 // 0号节点的左节点为2号节点,右节点为5号节点
-1 -1 // 1号节点左右节点都为空
1 4 // 2号节点左节点为1号节点,右节点为4号节点
-1 -1 // ...依次类推
-1 -1
-1 3
输出
2 // 1号节点和4号节点在上述树结构中的祖先节点为2号节点
思路分析
-
所谓祖先节点一定是我们的目标节点或在它的上层,也就是我们得把当前节点的下面部分遍历完,才能判断当前节点是不是祖先节点。
在树的三种遍历中,先把下面遍历完在判断当前节点的遍历方式显而易见,是后序遍历,确定遍历方式是解决问题的第一步。
-
第二步是设立边界,即怎样判断当前节点是不是祖先节点,或者怎样确定它一定不是祖先节点
- 如果当前节点左子树部分存在目标节点,右子树部分也存在目标节点,那么可以确定当前节点一定是祖先节点
- 如果当前节点是目标节点,且左右子树中也存在一个目标节点,则可以确定当前节点一定是祖先节点
- 除上述两种情况外,其余情况皆为非祖先节点
-
明确步骤之后,我们设计的函数应当返回当前节点左右子树或自身是否包含目标节点,若包含返回
true,不包含返回false,并且在后序遍历过程中记录下满足条件的祖先节点。
代码实现
package homework;
import java.util.Scanner;
public class Main {
static int ans = -1;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
TreeNode arrs[] = new TreeNode[n];
int k1 = scanner.nextInt();
int k2 = scanner.nextInt();
for (int i = 0; i < n; i++) {
TreeNode node = new TreeNode();
node.left = scanner.nextInt();
node.right = scanner.nextInt();
arrs[i] = node;
}
findAncestorByPostOrder(arrs, 0, k1, k2);
System.out.println(ans);
}
public static boolean findAncestorByPostOrder(TreeNode arrs[], int index, int k1, int k2) {
if (index == -1) {
return false;
}
boolean left = findAncestorByPostOrder(arrs, arrs[index].left, k1, k2);
boolean right = findAncestorByPostOrder(arrs, arrs[index].right, k1, k2);
// 说明当前节点是目标之一
boolean flag = index == k1 || index == k2;
// 当前节点为目标节点主要对应如下两种情况:
// 1. 当左右同时为目标;
// 2. 当左边或者右边有一个为目标,且当前也是目标之一
if ((left && right) || ((left || right) && flag)) {
ans = index;
}
// 如果当前节点左右存在目标节点,或者当前节点就是目标节点时返回 true
return left || right || flag;
}
}
class TreeNode {
int left;
int right;
}