数据结构:复杂度的练习(笔记)
例题一:
可以先给数组排序,然后再创建一个i值,让他循环一次++一次,遍历这个排序后的数组,但如果用qsort函数进行排序,时间复杂度就和题目要求的不一致了。所以这个方法行不通
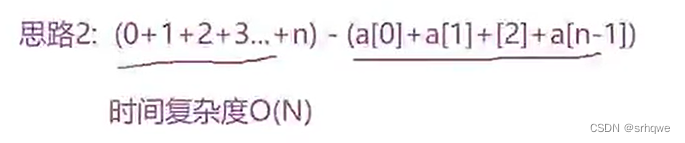
可以将0-n的整数全部相加,然后减去数组中的每个元素,那么就会得到缺失的那个数,此时也会发现时间复杂度是O(N),符合题目的要求。所以这个方法可以
可以创建一个数组arr2,将题目给的数组arr1内的数字 作为arr2的下标,并且将值放进去。最后如果发现arr2数组内那个坐标没有值,那么就是哪个数。发现时间复杂度也是O(N)。所以这个方法也可以。
这里将arr1放入arr2,需要循环N次,在这个循环外,需要遍历arr2中缺失的那个数,又需要N次,因此F(N) = 2N 那么时间复杂度就是:O(N)
相比与思路2,思路3略比逊色。
异或:相同位0.不同为1
两个相同的数字异或是0:x^x=0
因此,x先和[0,n]异或,就会拿到[0,n]这些数字,也就是x就会被赋予这些数字。当这些数字,再在有缺失的数组中异或,得到的就会是哪个缺失的数字。
无论数组中的数字是不是[0.n]的顺序,只要期间内和相同的数字异或,那么就会是0。
如:x^y^b^a^y^a^b==x^y^y^a^a^b^b==x^0^0^0==x(缺失的那个数)
因此,无论x先和谁异或,只要相同的两个数异或过,那么就相当于异或上0,也就是会被消掉。
最后时间复杂度:O(N)
就用思路4来写一段代码:
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> int main() { int arr1[] = { 9,0,1,8,4,6,5,3,7};//缺失2 int x = 0; int n = sizeof(arr1) / sizeof(arr1[0]);//题目中的n是给定的,不算入时间复杂度。 for (int i = 0; i <= n; i++) { x ^= i; i != n ? x ^= arr1[i] : NULL ;//防止越界访问 } printf("%d\n", x); //结果:2 return 0; }i != n ? x ^= arr1[i] : NULL ;使用的是三目运算符(条件运算符),当i==n时,arr1并没有arr1[n]元素,如果访问了,就是越界访问,会出现问题。因此当i==时,执行NULL,也就是不执行。
例题二:

对于这道题,有单独的文章:
C语言题目:左旋字符串._srhqwe的博客-CSDN博客
方法一(对应C语言题目:左旋字符串._srhqwe的博客-CSDN博客的方法一):
空间复杂度是O(1) :因为空间是可以重复利用的,tmp被释放掉,然后又用tmp。
时间复杂度是O(N*K):保存变量,然后旋转n-1次,就是N,其中要执行K次,所以是K*N。
方法二:

开辟一块空间(数组)tmp,将要旋转的个数,对应nums元素的位置,然后直接放到tmp数组,在把nums剩下的元素,再放到tmp数组。
如此,时间复杂度是O(N) 空间复杂度是O(N),但题目要求空间复杂度是O(1),因此这里并不符合题目的要求。
方法三(三步反转法:对应C语言题目:左旋字符串._srhqwe的博客-CSDN博客的方法二):

时间复杂度是:O(N)
空间复杂度是:O(1)
因为方法1和3在另一篇文章都有,就写一遍方法2,但是!方法2并不符合题目要求。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9 };
int tmp[20] = { 0 };
int sz = sizeof(arr) / sizeof(arr[0]);//元素个数
int k = 3;//假如要向左旋转的字符个数为3
for(int i = 0;i<sz-k;i++)//将arr后6个,放到tmp的前6个当中
{
tmp[i] = arr[k + i];
}
for (int i = 0; i <k ; i++)//将arr前3个,放到tmp后3个中
{
tmp[sz - k + i] = arr[i];
}
for (int i = 0; i < sz; i++)//打印tmp的每个元素
{
printf("%d ", tmp[i]);
//结果:4 5 6 7 8 9 1 2 3
}//实现反转
return 0;
}