来源：力扣（LeetCode）

描述：

你正在经营一座摩天轮，该摩天轮共有 4 个座舱 ，每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱，但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。

给你一个长度为 n 的数组 customers ， customers[i] 是在第 i 次轮转（下标从 0 开始）之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ，一旦该座舱再次抵达地面，他们就会离开座舱结束游玩。

你可以随时停下摩天轮，即便是 在服务所有游客之前 。如果你决定停止运营摩天轮，为了保证所有游客安全着陆，将免费进行所有后续轮转 。注意，如果有超过 4 位游客在等摩天轮，那么只有 4 位游客可以登上摩天轮，其余的需要等待 下一次轮转 。

返回最大化利润所需执行的 最小轮转次数 。 如果不存在利润为正的方案，则返回 -1 。

示例 1：

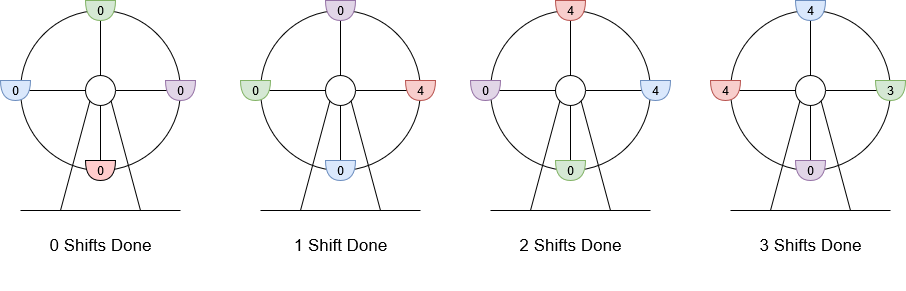
输入：customers = [8,3], boardingCost = 5, runningCost = 6
输出：3
解释：座舱上标注的数字是该座舱的当前游客数。
1. 8 位游客抵达，4 位登舱，4 位等待下一舱，摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14 。
2. 3 位游客抵达，4 位在等待的游客登舱，其他 3 位等待，摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28 。
3. 最后 3 位游客登舱，摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37 。
轮转 3 次得到最大利润，最大利润为 $37 。

示例 2：

输入：customers = [10,9,6], boardingCost = 6, runningCost = 4
输出：7
解释：
1. 10 位游客抵达，4 位登舱，6 位等待下一舱，摩天轮轮转。当前利润为 4 * $6 - 1 * $4 = $20 。
2. 9 位游客抵达，4 位登舱，11 位等待（2 位是先前就在等待的，9 位新加入等待的），摩天轮轮转。当前利润为 8 * $6 - 2 * $4 = $40 。
3. 最后 6 位游客抵达，4 位登舱，13 位等待，摩天轮轮转。当前利润为 12 * $6 - 3 * $4 = $60 。
4. 4 位登舱，9 位等待，摩天轮轮转。当前利润为 * $6 - 4 * $4 = $80 。
5. 4 位登舱，5 位等待，摩天轮轮转。当前利润为 20 * $6 - 5 * $4 = $100 。
6. 4 位登舱，1 位等待，摩天轮轮转。当前利润为 24 * $6 - 6 * $4 = $120 。
7. 1 位登舱，摩天轮轮转。当前利润为 25 * $6 - 7 * $4 = $122 。
轮转 7 次得到最大利润，最大利润为$122 。

示例 3：

输入：customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
输出：-1
解释：
1. 3 位游客抵达，3 位登舱，0 位等待，摩天轮轮转。当前利润为 3 * $1 - 1 * $92 = -$89 。
2. 4 位游客抵达，4 位登舱，0 位等待，摩天轮轮转。当前利润为 is 7 * $1 - 2 * $92 = -$177 。
3. 0 位游客抵达，0 位登舱，0 位等待，摩天轮轮转。当前利润为 7 * $1 - 3 * $92 = -$269 。
4. 5 位游客抵达，4 位登舱，1 位等待，摩天轮轮转。当前利润为 12 * $1 - 4 * $92 = -$356 。
5. 1 位游客抵达，2 位登舱，0 位等待，摩天轮轮转。当前利润为 13 * $1 - 5 * $92 = -$447 。
利润永不为正，所以返回 -1 。

提示：

• n == customers.length
• 1 <= n <= 10⁵
• 0 <= customers[i] <= 50
• 1 <= boardingCost, runningCost <= 100

方法：模拟

假设每位游客需要支付的费用是 boardingCost，一次轮转有 curCustomers 位游客登上座舱，每次轮转的运行成本是 runningCost，则摩天轮当前一次轮转的利润是 boardingCost × curCustomers − runningCost，其中boardingCost 和 runningCost 的值是已知的，curCustomers 的值由正在等摩天轮的游客的数量和座舱可以容纳的游客的数量中的最小值决定，其中座舱可以容纳的游客的数量为 4。

对于长度为 n 的数组 customers，customers[i] 是在第 i 次轮转之前到达的新游客的数量（i 从 0 开始），因此可以根据到达的新游客的数量和登上摩天轮的游客的数量计算每一次轮转时正在等摩天轮的游客的数量。

轮转摩天轮分成两个阶段。第一阶段是前 n 次轮转，每次轮转之前都可能有新游客到达。如果在第一阶段结束之后还有剩余的游客在等摩天轮，则进入第二阶段，将剩余的游客轮转完毕。

对于第一阶段的每次轮转，需要首先计算该次轮转时正在等摩天轮的游客的数量，然后计算该次轮转的利润以及总利润，同时维护最大利润与最大利润的最小轮转次数。具体而言，第 i 次轮转的流程如下：

1. 使用 customers[i] 的值更新正在等摩天轮的游客的数量；
2. 计算登上座舱的游客的数量，为正在等摩天轮的游客的数量和座舱可以容纳的游客的数量的最小值；
3. 将登上座舱的游客的数量从正在等摩天轮的游客的数量中减去；
4. 计算该次轮转的利润，并计算到该次轮转的总利润；
5. 如果总利润大于最大利润，则更新最大利润与最大利润的最小轮转次数。

第一阶段结束后，如果没有剩余的游客在等摩天轮，则直接返回最大利润的最小轮转次数。如果还有剩余的游客在等摩天轮，只有当剩余的游客带来的利润为正时，才需要考虑第二阶段，可能获得更多的利润。

由于每位游客需要支付的费用是正数，因此当座舱满舱时（即座舱上有 4 位游客，达到最大容纳数量），可以达到一次轮转的最大利润。如果一次轮转的最大利润不为正，则第二阶段的利润一定不为正，因此直接返回第一阶段的最大利润的最小轮转次数。

如果一次轮转的最大利润为正，则每次座舱满舱的轮转的利润都为正，因此计算全部满舱轮转之后的总利润，如果大于最大利润则更新最大利润与最大利润的最小轮转次数。最后可能剩下少于 4 位游客，需要进行最后一次非满舱的轮转，在最后一次轮转之后计算总利润，如果总利润大于最大利润则更新最大利润与最大利润的最小轮转次数。

代码：

class Solution {
public:
    int minOperationsMaxProfit(vector<int>& customers, int boardingCost, int runningCost) {
        int ans = -1;
        int maxProfit = 0;
        int totalProfit = 0;
        int operations = 0;
        int customersCount = 0;
        int n = customers.size();
        for (int i = 0; i < n; i++) {
            operations++;
            customersCount += customers[i];
            int curCustomers = min(customersCount, 4);
            customersCount -= curCustomers;
            totalProfit += boardingCost * curCustomers - runningCost;
            if (totalProfit > maxProfit) {
                maxProfit = totalProfit;
                ans = operations;
            }
        }
        if (customersCount == 0) {
            return ans;
        }
        int profitEachTime = boardingCost * 4 - runningCost;
        if (profitEachTime <= 0) {
            return ans;
        }
        if (customersCount > 0) {
            int fullTimes = customersCount / 4;
            totalProfit += profitEachTime * fullTimes;
            operations += fullTimes;
            if (totalProfit > maxProfit) {
                maxProfit = totalProfit;
                ans = operations;
            }
            int remainingCustomers = customersCount % 4;
            int remainingProfit = boardingCost * remainingCustomers - runningCost;
            totalProfit += remainingProfit;
            if (totalProfit > maxProfit) {
                maxProfit = totalProfit;
                operations++;
                ans++;
            }
        }
        return ans;
    }
};

执行用时：76 ms, 在所有 C++ 提交中击败了96.77%的用户
内存消耗：79.4 MB, 在所有 C++ 提交中击败了93.55%的用户
复杂度分析
时间复杂度：O(n)，其中 n 是数组 customers 的长度。遍历数组一次计算第一阶段的最大利润与最小轮转次数，时间复杂度是 O(n)，第二阶段的最大利润与最小轮转次数的计算的时间复杂度是 O(1)。
空间复杂度：O(1)。只需要维护常量的额外空间。
author：LeetCode-Solution