原根

• 什么是原根？
  设 （a,m）= 1, 并且$a^e$ 三 1 (mod m) ，则我们称：$or{d}_m$(a) = e，ord也叫做群论，也可以叫阶。假如：$or{d}_m(a)$ = $\varphi (m)$，那么我们就称a是模m的原根。

• 原根又称：本原元，生成元

• 对ord的解释：ord就是表示a的阶，是使$a^e$ 三 1 (mod m)成立的最小的数，e要在1-(m-1)的范围内找，必然有一个数能满足式子的，因为至少来说你可以使用欧拉定理$a^{\varphi }$${}^{(}$${}^m$${}^{)}$ 三 1 (mod m)

• 我对原根的理解方式：a，m互素，并且ord = e为最小使$a^e$ 三 1 的数字，然后在$a^e$ 三 1 (mod m)中的e要等于$\varphi (m)$的时候就称a是m的一个原根，这里用把e用$\varphi (m)$替换掉之后就变成了欧拉函数：$a^{\varphi }$${}^{(}$${}^m$${}^{)}$ 三 1 (mod m)，本质就是在保证其他限制条件满足的情况下，主要要满足的就是当e等于$\varphi (m)$，简而言之，e是能满足式子的最小数字，但他又是欧拉函数，在素数中容易让我混淆，因为假如a是素数，那么欧拉函数就是素数-1，因此我时不时会觉得该数字既是最小也是最大。但仔细想想后其实是满足同余1的最小数字，因为最大的数字才满足该条件，就是最小的数字满足同余1的，那么前面的数字必然是能够使$a^e$重新组成一个简化剩余系（也是群），也就是前面的都不是余1的且不同余数 。

• ❀ a必须是模m的简化剩余系 ❀

• 原根可以不存在，但阶一定存在。

原根在后面的密码的加密解密中大有用处

• 如何求原根？
  不难发现，在上面模m的时候，数字其实a的范围就限制在了1 ~ (m-1) 的范围内，因为a是模m的简化剩余系，并且无论a数字多大终究会以模m的形式进行计算，所以我们找原根最原始的办法就是从1开始找，1必然不是原根，因为简化剩余系范围内，第一个数字1就能使1同余1，因此1不会是式子的原根。自此，我们开始往后找，假设m是素数，那么就是找2,3,4,5…m-1，一个个尝试。
  $2^1$,$2^2$,$2^3$,$2^4$…$2^m$${}^{-}$${}^1$ mod m
  $3^1$,$3^2$,$3^3$,$3^4$…$3^m$${}^{-}$${}^1$ mod m
  $4^1$,$4^2$,$4^3$,$4^4$…$4^m$${}^{-}$${}^1$ mod m
  …
  …
  …
  直到m-1
  如果有一个数字a满足：$a^{\varphi }$${}^{(}$${}^m$${}^{)}$ 三 1 (mod m)就是原根。

• 把原根的所有阶都算出来，其结果是模数m的简化剩余系，比如 ↓
  

• 总结：
  由于在模的世界中进入计算后最大的数字大不过模数。假设模数为m，那么原根是在m的简化剩余系中找，同理 ，因为模m，所以阶(e)的范围是在1-(m-1) 范围内，即使超出了，在后面会讲到其实阶也能进行模运算后再进入计算。然后就是利用一些技巧计算出在该范围内哪一些是原根了。后面继续学习方法技巧。

一些求原根的定理↓

$or{d}_m(a)$ | $\varphi (m)$

观察上图会发现能使1-6同余1的阶是：1 3 6 6 2，而这些数字都是$\varphi (m)$的因子。
因此我们在找原根的时候就可以：①先算出欧拉函数②分解出欧拉函数的因子③不用1-6的(e)阶去算(a)作为简化剩余系的数字，只需要用e是欧拉函数的因子去算(a)简化剩余系底数，满足定义就是原根。上图中的3 5就是模7的原根。

• 该定理反过来可以进一步推敲：
  因为$\varphi (m)$是必然会使a同余1，假设 $a^d$ 三 1 (mod m) ，
  那么$or{d}_m(a)$ | d，因为ord是最小的，在一个a（a是我们在简化剩余系中找的一个数），假如不是原根，d必然比ord大，因此是d的因子，上面提到的使同余1的阶都是$\varphi (m)$的因子，即使d不是$\varphi (m)$但是因子之间必然也是倍数关系。
• 几个简单性质
  
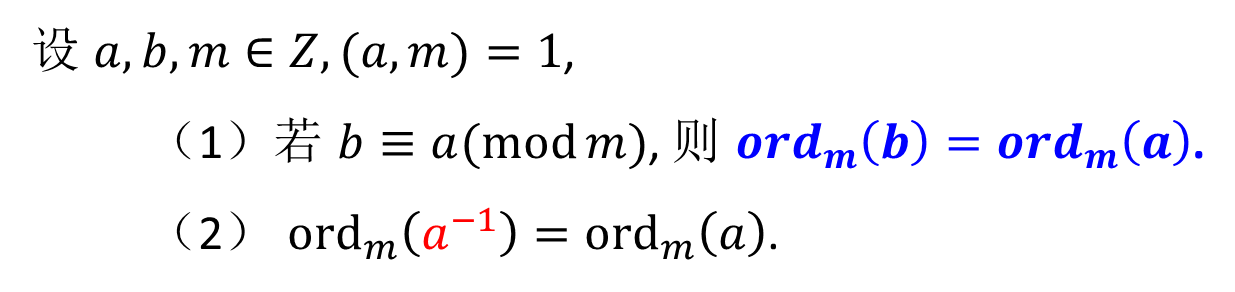
• 利用原根查表求逆
  
  
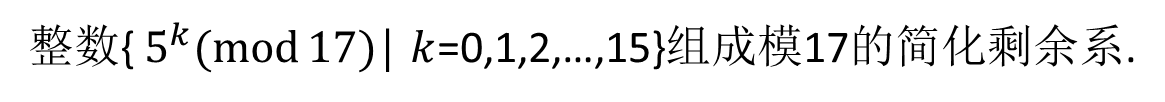
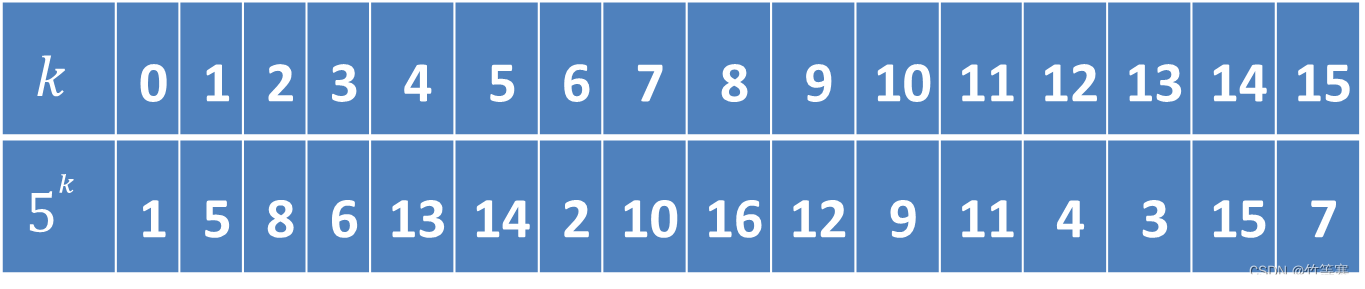
  假设我们求：$8^{-}$${}^1$ (mod 17)
  对应在表中，8是对应着$5^2$，也就是求($5^2$)${}^{-}$${}^1$
  $5^{-}$${}^2$ × $5^1$${}^6$ = $5^1$${}^4$，那么$5^1$${}^4$的阶14对应着表中的15，所以$8^{-}$${}^1$ 是 15。若已知原根表，我们无须复杂计算即可求出一个数的逆元。
  （为什么乘以$5^1$${}^6$：因为$\varphi (17)$ = 16，$a^{\varphi }$${}^{(}$${}^m$${}^{)}$ = 1，所以直接乘以$5^1$${}^6$相当于乘1）

原根和阶的关系

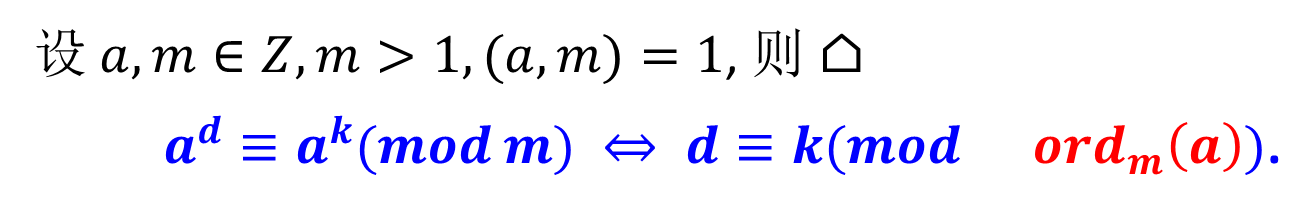
解释：因为ord是最小数能使a同余1，既然d , k 是同余的，那么必然超出一轮a阶次幂计算中，就好比2模3等于2,5模3也等于2,3和5就是过了一轮模数。
再来一个循环例子：11211211，假设第一个数字为1，那么第四个数字也是1，在该循环中，循环的是112，因此也是过了一轮循环。阶的关系也是类似的。
下面是推论：

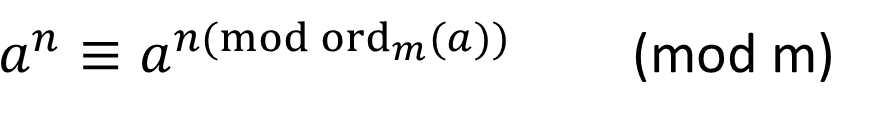
• 阶的性质定理
  

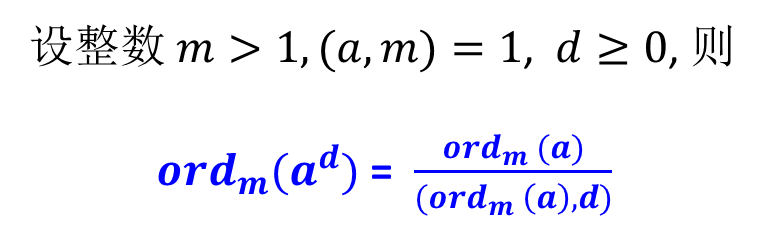
解释：背熟吧，我脑力不够理解不了。
下面是推论：

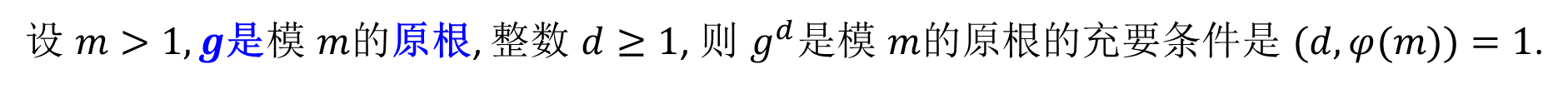
解释：因为已知了g是原根，再加上在上面性质中，ord和d是互素的话，那么最大公因数为1，所以ord $a^d$ = ord a,分母为1。已知g是原根前提下，ord必然等于$\varphi (m)$，所以$\varphi (m)$ = ord。推论就是这么来的。

• 从上述推论得出结论
  但凡我们找到了一个原根，想要找出其他原根的时候就不再需要继续往下一个一个乘以$\varphi (m)$的因子了，这时候我们利用($or{d}_m(a)$，d)=1互素的性质，当两个互素的时候就是$or{d}_m$(a${}^d$) = $or{d}_m(a)$,也就是说a${}^d$ 也为原根，我们反过去推敲，就知道我们只需要找一个d与原根的阶互素即可，原根的阶必然是$\varphi (m)$，所以与$\varphi (m)$互素的d，就是能使a${}^d$ 也为原根的条件。

• 原根个数
  

• 素数原根
  

---

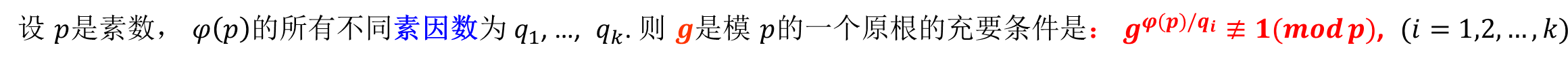
• 再次总结：
  因为太乱了，我必须出手整理一下整个流程给自己复习。

• 开始
  初识原根，原根是模m的简化剩余系中的成员。
  设原根a，次方数为e，
  a可能是简化剩余系中任何一个数字，e的范围是[1,m-1]
  a作为简化剩余系，每个数字都要从遍历e，即：$a^e$，
  从中找到能使$a^e$ 三 1，
  假如一个简化剩余系中的某个数字a有多个能使$a^e$ 三 1，那么这位简化剩余系中的数字a并不是我们找的原根。
  原根需要使$a^e$ 三 1，同时1~m-1中只有，唯有，唯一有一个数e，且e = $\varphi (m)$，这时候就是原根了
  a计算完后继续换下一个简化剩余系中的数字计算，步骤也是上面的步骤，只要出现了$a^e$ 三 1的e不等于$\varphi (m)$就不用再继续往高次幂算了，直接判断该数字不是原根

• 进阶方法：稍微简化了求原根的步骤
  求出$\varphi (m)$后，找出$\varphi (m)$的因子组成数字，这些因子组成数字就是有可能作为e使$a^e$同余1
  只需要把这些因子作为次方数即可，不用再从e的范围[1-,m-1]这么大的范围中依次乘进去，计算量太大了
  如果这些因子作为e都不能使$a^e$ 三 1，那么就可以确定a就是原根。
  但是我们找出一个原根后，后面还可能会有很多不同的，这时候我们再重复上面的步骤慢慢从简化剩余系中找。

• 史诗级连锁反应求原根
  认识阶：
  上述我们的当$a^e$ 三 1的时候 e就叫做阶，切记，这里没有要求e要和$\varphi (m)$相等，也就是e从1-(m-1)，从小到大开始递增次方数找原根的时候，找到了就是叫做阶，同时因为是从小到大开始找，所以阶也叫是“最小整数”使$a^e$同余1.
  知道阶的定义之后，我们只需要按照进阶方法找出一个原根后，
  找出与$\varphi (m)$互素的数字，该数字范围一般是非负且比$\varphi (m)$小的数字。
  然后用找到的一个原根a遍历这些与$\varphi (m)$互素且比$\varphi (m)$小的数字，遍历之后的每一个数字模m后就是所有原根了。

• 完美收工

---