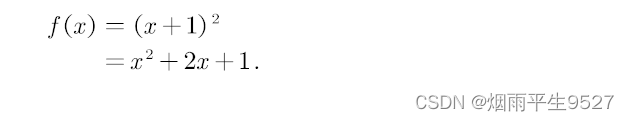作者的话
作为一个文本排版工具,latex一直以来都备受科研工作者、学生和出版社的青睐。但是对于初学者来说,latex的学习曲线可能会有些陡峭。因此,我写这篇博客旨在为初学者提供一个简单易懂的latex教程,让大家能够快速入门并掌握基本的排版技巧。希望这篇博客能够帮助到大家,如果你有任何问题或者建议,欢迎在评论区留言,同时也希望大家能够三连支持,谢谢!
一、latex源文件基本结构
LaTeX 源文件的基本结构包括以下几个部分:
1.文档类声明:通过指定文档类来定义文档的基本格式和样式。例如,声明文档类为 article:
\documentclass{article}2.导言区:在导言区中可以设置文档的全局属性,引用宏包,定义命令和环境等。例如,导入常用的宏包和自定义命令:
\usepackage{graphicx}
\newcommand{\mycommand}{Some text}
3.正文部分:正文部分是文档的主体内容,包括标题、段落、列表、图片、表格等。例如,插入一张图片和一个表格:
% 文档正文
\begin{document}
% 标题、作者等信息
\title{标题}
\author{作者}
\date{日期}
\maketitle
% 目录
\tableofcontents
% 正文
\section{章节标题}
\subsection{小节标题}
正文内容
% 结束正文
\end{document}4.结束语句:在文档的末尾需要添加结束语句以告诉 LaTeX 编译器文档已经结束。例如:
\end{document}二、数学公式初步
2.1行内公式
LaTeX 中有多种方法可以排版行内公式。以下是其中一些常用的方法:
使用一对美元符号 $ 将公式包裹起来,例如: $y = mx + b$。这是最常用的方法。
使用一对小括号 () 将公式包裹起来,例如: \(y = mx + b\)。
使用一对斜杠 \[ \] 将公式包裹起来,例如: \[y = mx + b\]。这种方式可以用于排版独立的行间公式。
2.2上标和下标
在 LaTeX 中,上标和下标是常用的数学符号,用于表示某些变量或常数的指数或下标。下面详细介绍 LaTeX 中的上标和下标的用法:
上标
使用 ^ 符号来表示上标。例如,x^2 表示 $x$ 的平方。
如果要上标的内容是多个字符,可以用一对花括号 {} 将其括起来。例如,a^{n-1} 表示 $a$ 的 $n-1$ 次方。
上标的内容可以是任意的数学表达式,包括分数、根式等。例如,\frac{1}{2}^2 表示 $\frac{1}{2}$ 的平方。
如果需要添加多个上标,可以使用一对花括号 {} 来区分不同的上标。例如,x^{2n}_{k+1} 表示 $x$ 的第 $k+1$ 个下标上面的 $2n$ 次方。
下标
使用 _ 符号来表示下标。例如,x_1 表示 $x$ 的第一个下标。
如果需要添加多个下标,可以使用一对花括号 {} 来区分不同的下标。例如,a_{i,j,k} 表示 $a$ 的第 $i,j,k$ 个下标。
下标的内容可以是任意的数学表达式,包括分数、根式等。例如,a_{\frac{1}{2}} 表示 $a$ 的下标是 $\frac{1}{2}$。
如果要下标的内容是多个字符,可以用一对花括号 {} 将其括起来。例如,x_{n-1} 表示 $x$ 的第 $n-1$ 个下标。
注意:
如果上标或下标的内容较长,可以使用 \mathrm{} 或 \text{} 命令来保证其正常显示。例如,x_{\mathrm{max}} 表示 $x$ 的下标是“max”。
在使用多个上标或下标时,需要使用一对花括号 {} 来区分不同的上标或下标,否则会出现错误。
如果需要同时使用上标和下标,可以使用一对花括号 {} 来区分不同的上标和下标。例如,x^{2n}_{k+1} 表示 $x$ 的第 $k+1$ 个下标上面的 $2n$ 次方
2.3希腊字母
在 LaTeX 中,可以使用希腊字母来表示各种数学符号和变量。下面列出了 LaTeX 中常用的希腊字母及其对应的命令:
这些命令可以在数学环境中使用,例如在 $...$ 或 \[...\] 中。例如,输入 \alpha+\beta=\gamma 将会得到 。
2.4数学函数
下面是常见数学函数的表格及其LaTeX代码和含义:
| 函数 | LaTeX | 含义 |
|---|---|---|
| 平方根 | ‘\sqrt{x}’ | |
| 立方根 | ‘\sqrt[3]{x}’ | |
| 向上取整 | ‘\lceil x \rceil’ | |
| 向下取整 | '\lfloor x \rfloor' | |
| 绝对值 | ‘\left| x \right|’ | |
| 自然对数 | ‘\ln x’ | |
| 以10为底的对数 | '\log x' | |
| 以a为底的对数 | '\log_a x' | |
| 正弦函数 | '\sin x' | |
| 余弦函数 | '\cos x' | |
| 正切函数 | '\tan x' | |
| 余切函数 | '\cot x' | |
| 正割函数 | '\sec x' | |
| 余割函数 | '\csc x' | |
| 反正弦函数 | '\arcsin x' | |
| 反余弦函数 | '\arccos x' | |
| 反正切函数 | ' |
这些函数可以在数学环境中使用,需要使用$...$或\[...\]进行数学模式。例如,\sin x将生成正弦函数的符号。
2.5分式
在LaTeX中,可以使用\frac{numerator}{denominator}命令来创建分式。其中,numerator表示分子,denominator表示分母。例如,\frac{1}{2}可以生成一个的分数。
2.6行间公式
LaTeX的行间公式使用$$ equation $$或\begin{equation} equation \end{equation}命令创建,一般独占一行。公式的大小、字体、对齐等样式与周围的文本不同。在行间公式中,可以使用各种数学符号和命令,例如上下标、分式、根号、求和符号等等。公式中的上下标、根号等符号比行内公式中更大,以便更清晰地显示公式内容。
2.7求和函数和求积函数
LaTeX中,求和公式和求积公式可以用\sum和\prod命令创建。
求和公式:
格式:\sum_{下标起始值}^{下标结束值} 被求和的表达式
示例:$$ \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6} $$
效果:
求积公式:
格式:\prod_{下标起始值}^{下标结束值} 被求积的表达式
示例:$$ \prod_{n=1}^{\infty} \left(1 + \frac{1}{n}\right)^n = e^\frac{1}{2} $$
效果:
在上述示例中,下标起始值和下标结束值可以是任何数学表达式,例如常数、变量、函数等。求和公式和求积公式中的表达式可以包括各种数学符号和函数。
2.8矩阵
在LaTeX中,矩阵可以使用matrix环境来创建。下面是一个示例:
在矩阵环境,用&分隔列,用\\分隔行
\begin{matrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{matrix}该代码将生成一个 的矩阵,如下所示:
如果你想为矩阵添加括号,请使用bmatrix(方括号)、pmatrix(圆括号)、Bmatrix(大括号)、vmatrix(单竖线)或Vmatrix(双竖线)环境例如
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix}
生成
在矩阵中可以使用各种数学符号、上下标、分数等等。例如,下面的代码生成了一个含有上下标和分数的矩阵:
\begin{bmatrix}
a_{11} & \frac{a_{12}}{2} & a_{13} \\
a_{21} & a_{22}^{2} & a_{23} \\
a_{31}^{3} & a_{32} & a_{33}
\end{bmatrix}生成
矩阵中还可以使用省略号来表示一些元素的省略,其中 \dots 表示水平省略号,\vdots 表示垂直省略号,\ddots 表示对角省略号。
\begin{pmatrix}
1 & 2 & \dots & n \\
2 & 5 & \dots & 2n \\
\vdots & \vdots & \ddots & \vdots \\
n & 2n & \dots & n^2 \\
\end{pmatrix}生成:
可用\times排版乘号


三角矩阵
在 LaTeX 中,三角矩阵可以通过 amsmath 宏包中的 matrix 环境和 bmatrix、pmatrix、vmatrix 等环境来创建。以 bmatrix 环境为例,示例如下:
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn}
\end{bmatrix}
生成
2.9多行数学公式
在 LaTeX 中,我们可以使用多种方式来排版多行数学公式。下面是几种常见的方式:
1.使用 equation 环境
equation 环境适用于单个数学公式,但是也可以用来排版多行公式。在 equation 环境中,使用 \nonumber 来标记不需要编号的行。示例如下
\begin{equation}
\begin{aligned}
f(x) &= (x + 1)^2 \\
&= x^2 + 2x + 1. \nonumber
\end{aligned}
\end{equation}生成
2.使用 align 环境
align 环境用于排版多行公式,可以使用 & 符号来对齐等号。示例如下:
\begin{align}
f(x) &= (x + 1)^2 \\
&= x^2 + 2x + 1.
\end{align}
生成
3.使用 split 环境
split 环境适用于将一个数学公式拆分成多行,可以与 equation、align、gather 等环境配合使用。示例如下:
\begin{equation}
\begin{split}
f(x) &= (x + 1)^2 \\
&= x^2 + 2x + 1.
\end{split}
\end{equation}
生成