题目描述

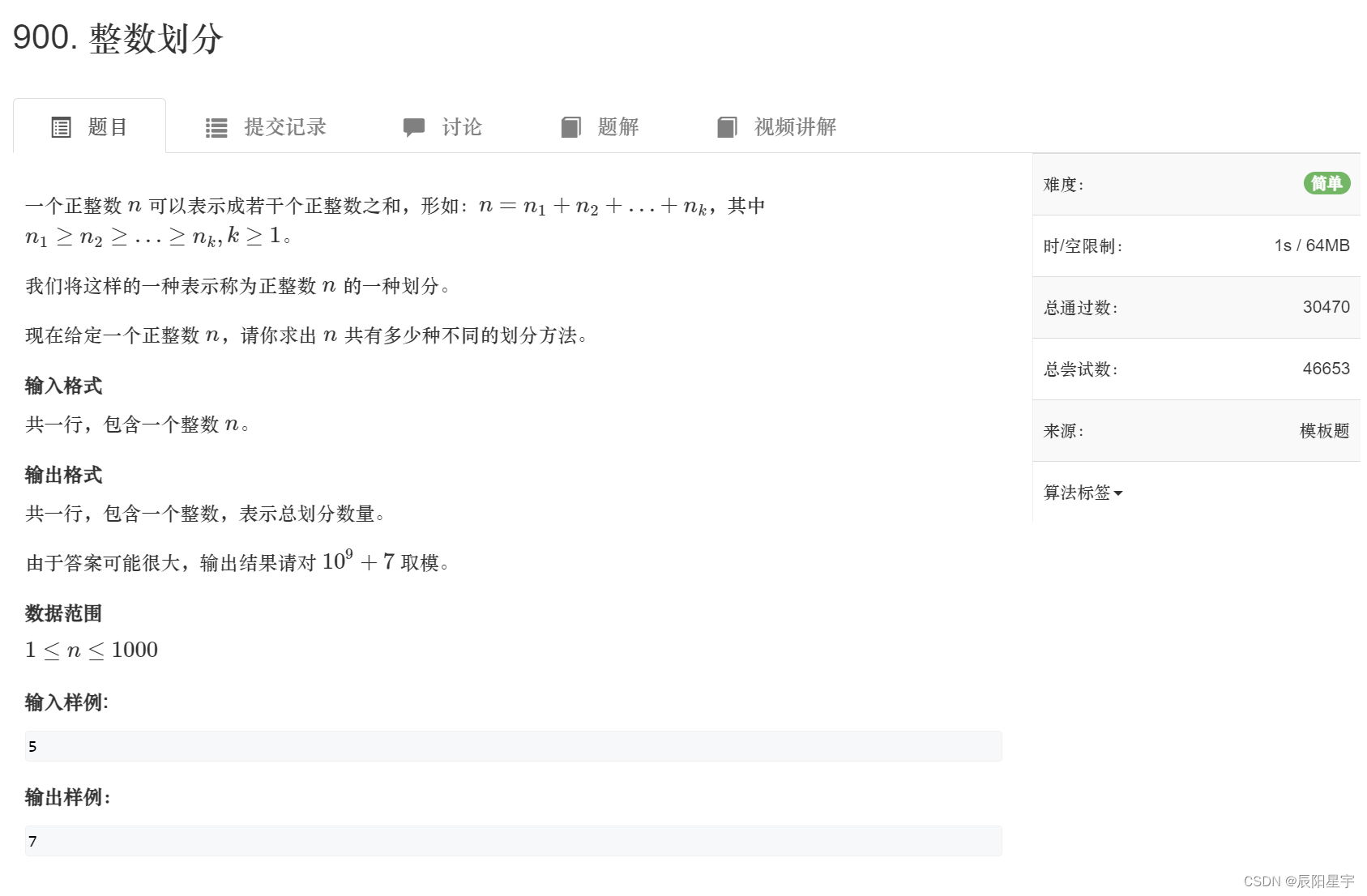
参考文章：900. 整数划分

解题思路

因为本题中规定了数字从大到小，其实也就是不论是1 + 2 + 1 = 4，还是2 + 1 + 1 = 4，都会被看作是2 + 1 + 1 = 4这一种情况，因此本题是在遍历中不考虑结果顺序。

背包问题中只需考虑使用的物品种类，因此可转化为完全背包问题，将组成的数看作物品且容量为1_{n，背包容量为n。本题便转化为了，从物品1}物品n（体积也是为1~n）中进行选择，构成背包容量为n的方案个数。

（1）完全背包二维数组

• 动态规划五步曲：

（1）dp[i][j]含义： 从1~i中选择物品，达到背包容量为j的方案个数。

（2）递推公式： $dp[i][j]=(dp[i-1][j]+dp[i][j-i])$，完全背包的一般性化简后递推公式，未化简前所表示的是尝试放入物品1到物品j后的情况。

（3）dp数组初始化： dp[i][0] = 1，容量为0时，仅有一种情况。

（4）遍历顺序： 从左到右，从上到下。

（5）举例： （省略）

#include <iostream>

using namespace std;

const int N = 1010, mod = 1e9 + 7;
int n;
int dp[N][N];


int main() {
    cin >> n;
    for(int i = 1; i <= n; i++)         dp[i][0] = 1;
    
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(i > j)           dp[i][j] = dp[i - 1][j] % mod;
            else                dp[i][j] = (dp[i - 1][j] + dp[i][j - i]) % mod;
        }
    }
    
    
    cout << dp[n][n] << endl;
    
    return 0;
}

（2）完全背包一维滚动数组

对变量进行优化

#include <iostream>

using namespace std;

const int N = 1010, mod = 1e9 + 7;
int n;
int dp[N];


int main() {
    cin >> n;
    dp[0] = 1;
    
    for(int i = 1; i <= n; i++) {
        for(int j = i; j <= n; j++) {
            dp[j] = (dp[j] + dp[j - i])  % mod;
        }
    }
    
    
    cout << dp[n] << endl;
    
    return 0;
}

（3）用加减1方法

此方法主要使用的是加一个和减一个1，还保持某种方案不变化的特点，得来递推公式。因为我们要求的只是方案个数，

例如：组合成3的方案可以为2、1和1、1、1，当我们想要得到组合成4的方案，那么就可以分别从2、1和1、1、1演化过来，就是2、1、1和1、1、1、1，此时3中这一部分含有最小值为1的方案个数与4中这一部分含有最小值为1的方案个数其实是相同的。

（1）dp[i][j]含义： 由j个数组合成总和为i的方案个数

（2）递推公式： $dp[i][j]=dp[i-1][j-1]+dp[i-j][j]$，将状态集合划分成两部分，一部分是j个数中的最小值值是1，另一部分是j个数中的最小值大于1。

对于最小值是1的集合，状态转移为$dp[i][j]=dp[i-1][j-1]$，意思为当前状态由少一个1的状态演变过来。因为我们要求的是组合成目标数是的方案个数，因此加上一个时，其实还是在此种方案下，故方案个数与dp[i - 1][j - 1]的方案个数相同。

对于最大值大于1的集合，状态转移为$dp[i][j]=dp[i-j][j]$，还是利用1这种特点，将j个数中各自减去一个1，此时dp[i][j]就可以有dp[i - j][j]而来。

（3）dp数组初始化： dp[0][0] = dp[1][1] = 1，重量为0和1时仅有一种方案。

（4）遍历顺序： 从左到右，从上到下。

（5）举例：

例如：组合成3的方案可以为2、1和1、1、1，当我们想要得到组合成4的方案，那么就可以分别从2、1和1、1、1演化过来，就是2、1、1和1、1、1、1，此时3中这一部分含有最小值为1的方案个数与4中这一部分含有最小值为1的方案个数其实是相同的。

#include <iostream>

using namespace std;

const int N = 1010, mod = 1e9 + 7;
int n;
int dp[N][N];

int main() {
    cin >> n;
    dp[0][0] = dp[1][1] = 1;
    
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= i; j++) {
            dp[i][j] = (dp[i - 1][j - 1] + dp[i - j][j]) % mod;
        }
    }
    
    int res = 0;
    for(int i = 1; i <= n; i++)     res = (dp[n][i] + res) % mod;
    
    
    cout << res << endl;
    
    return 0;
}