题目链接

Leetcode.2397 被列覆盖的最多行数 Rating ： 1719

题目描述

给你一个下标从 0 开始的 m x n二进制矩阵 mat和一个整数 cols，表示你需要选出的列数。

如果一行中，所有的 1 都被你选中的列所覆盖，那么我们称这一行 被覆盖 了。

请你返回在选择 cols列的情况下，被覆盖 的行数 最大 为多少。

示例 1：

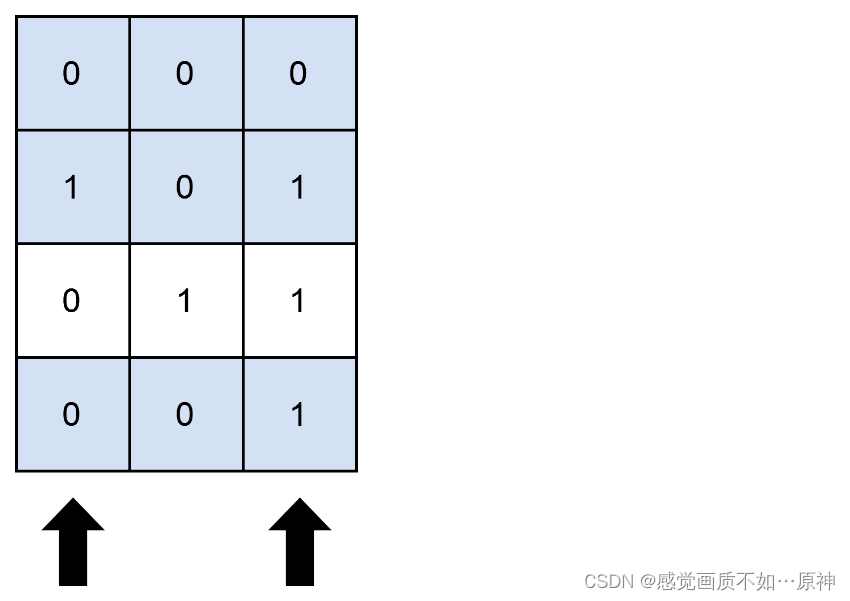
输入：mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
输出：3
解释：
如上图所示，覆盖 3 行的一种可行办法是选择第 0 和第 2 列。
可以看出，不存在大于 3 行被覆盖的方案，所以我们返回 3 。

示例 2：

输入：mat = [[1],[0]], cols = 1
输出：2
解释：
选择唯一的一列，两行都被覆盖了，原因是整个矩阵都被覆盖了。
所以我们返回 2 。

提示：

• $m==mat.length$
• $n==mat[i].length$
• $1<=m,n<=12$
• mat[i][j]要么是 0要么是 1。
• $1<=cols<=n$

分析：

一般题目给定的数据量在 [0,20]我们就要考虑能否使用 状态压缩 了。

对于每一行，我们都用一个二进制数 row[i]来表示。例如：1 1 1，三个位置都是 1就用 (111) = 7来表示。

也用一个二进制数 mask来表示要选的列，加入 mask的二进制表示，第 j位是 1的话，说明要选第 j列。否则不选第 j列。

我们只需要记录 bitCount(mask) == col的情况（ bitCount(mask) == col代表选了 col列）。此时再遍历每一行，如果 (mask & row[i] ) == row[i]，说明第 i行的所有的 1都被所选的列覆盖了，即第 i行是被完全覆盖了的。

时间复杂度：$O(m\ast n+m\ast 2^n)$

C++代码：

class Solution {
public:
    int maximumRows(vector<vector<int>>& matrix, int col) {
        int m = matrix.size() , n = matrix[0].size();
        vector<int> row(m);

        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                row[i] |= (matrix[i][j] << j);
            }
        }

        int ans = 0;
        for(int mask = 1;mask < (1 << n);mask++){
            if(__builtin_popcount(mask) == col){
                int cnt = 0;
                for(int j = 0;j < m;j++){
                    if((row[j] & mask) == row[j]) cnt++;
                }

                ans = max(ans,cnt);
            }
        }

        return ans;
    }
};

Java代码：

class Solution {
    private int bitCount(int x){
        int cnt = 0;
        while(x > 0){
            cnt++;
            x &= (x-1);
        }
        return cnt;
    }
    public int maximumRows(int[][] matrix, int cols) {
        int m = matrix.length;
        int n =  matrix[0].length;

        int[] row = new int[m];

        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                row[i] |= (matrix[i][j] << j);
            }
        }

        int ans = 0;
        for(int mask = 1;mask < (1 << n);mask++){
            if(bitCount(mask) == cols){
                int cnt = 0;
                for(int j = 0;j < m;j++){
                    if((mask & row[j]) == row[j]) cnt++;
                }
                ans = Math.max(ans,cnt);
            }
        }
        return ans;
    }
}