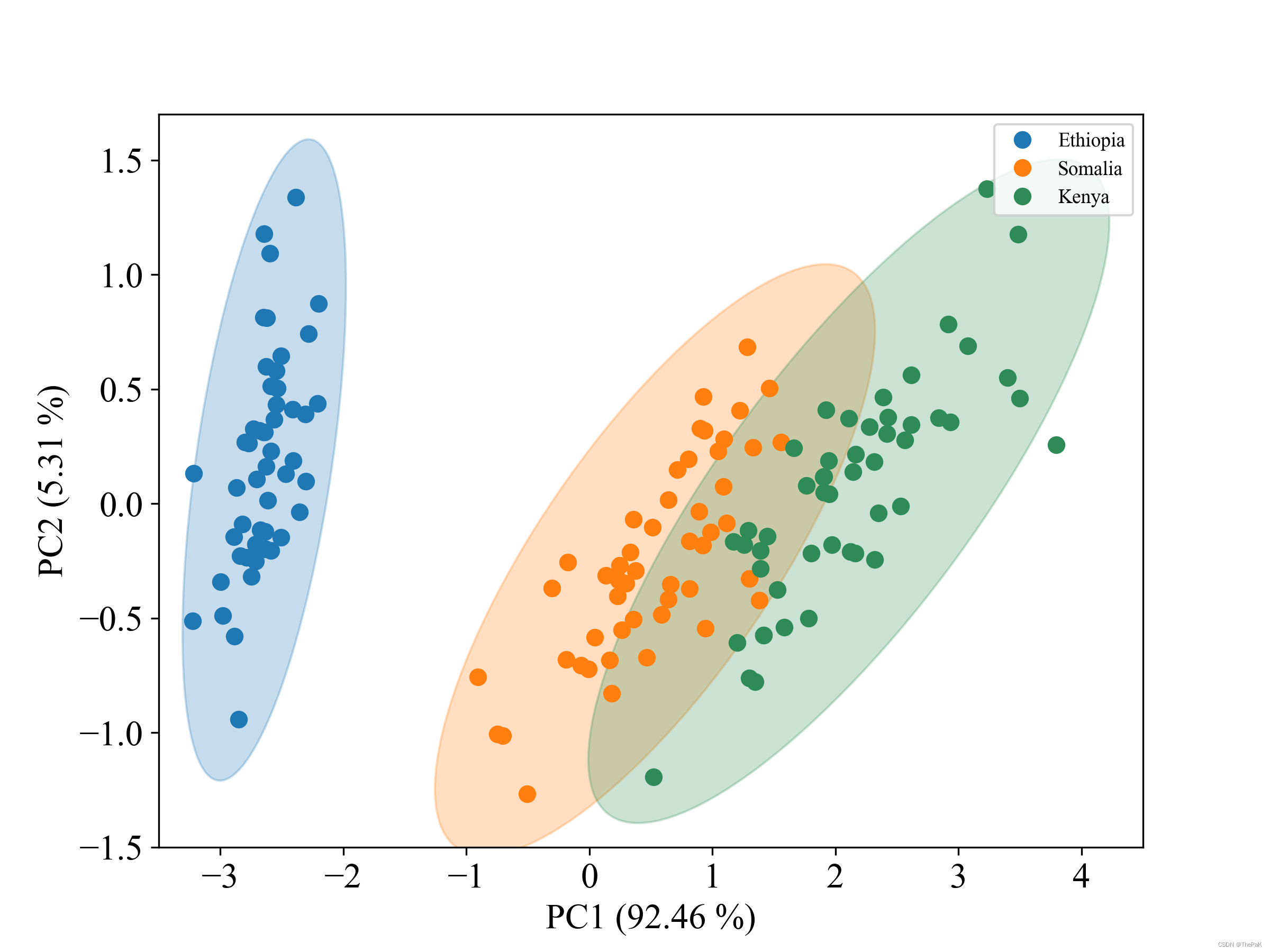
回溯法又叫回溯搜索法,是搜索的一种方式。
回溯法本质是穷举所有可能。如果想让回溯法高效一些,可以加一些剪枝操作。
回溯算法解决的经典问题:
组合问题
切割问题
子集问题
排列问题
棋盘问题
如何去理解回溯法?
回溯法解决的问题都可以抽象为树形结构,回溯法解决的是在集合中递归查找子集,集合的大小构成树的宽度,递归的深度构成树的深度。
递归就要有终止条件,所以必然是一颗高度有限的树(N叉树)
回溯法模板
回溯三部曲
回溯函数模板返回值以及参数(一般返回值都为void)
回溯函数终止条件
if(终止条件){
存放结果;
return;
}回溯搜索的遍历过程
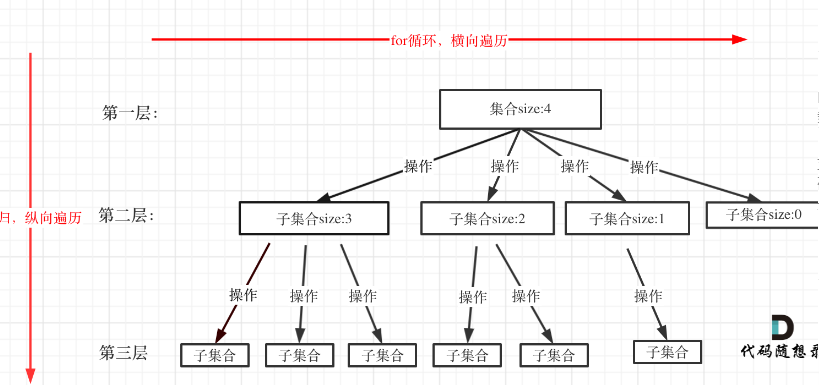
for(选择:本层集合中的元素(树中节点孩子的数量就是集合的大小)){
处理节点;
backtracking(路径,选择列表);//递归
回溯,撤销处理结果
}组合问题
组合
在for循环中,i的结束条件可以优化,即:
列表剩余元素个数n-i+1>=所需元素个数k-path.size(),i<=n-k+path.size()+1。
组合总和 | 无重复数 | 可重复取 |
组合总和II | 有重复数 | 不可重复取 |
组合总和III | 无重复数 | 不可重复取 |
组合总和IV | 无重复数 | 可重复取,且有排列(动规问题) |
组合总和III
电话号码的字组合
数字与字母的映射问题可以用map,也可以用一个二维数组;
将char型转为int型,用char-‘0’的方式。
组合总和
可以重复使用元素,所以startIndex直接等于i就行了,不能直接每次都从0开始(这是排列的情况,会有重复出现);
组合总和II
集合中出现了重复元素,如果用之前的常规做法,会出现下面重复的情况,因此需要去重工作。
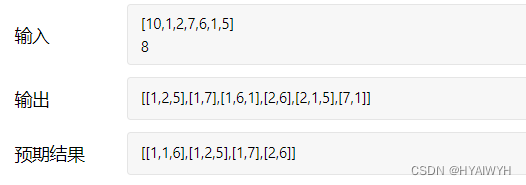
组合总和IV
用回溯超时了,是动态规划问题。
切割问题
分割回文串
如何切割的问题--确定分割点,例如abcdef,切割一个a后,在bvdef中再去切割第二段
如何判断为回文串--写一个bool型函数,专门用来判断
注意:截取子字符串substr(n,m)表示从下标n开始取m个元素。
复原IP地址
如何切割的问题,确定切割点,插入.号,用已经插入.号的数量来判断是否结束
如何判断是否为有效IP地址
注意一些细节问题:
string中插入 insert 擦除erase,因为已经插入.号,因此下一层递归开始应该在i+2处
除了只有一个0以外,以0开头的数字不合法;大于255不合法;
bool isValid(string& s,int left,int right){
if(left>right) return false;
if(s[left]=='0'&&left!=right) return false;
int x=stoi(s.substr(left,right-left+1));
if(x<=255) return true;
else return false;
}子集问题
子集 (不含重复元素)
子集问题是找树的所有节点,而组合和分割问题都是收集树的叶子节点。
每个节点都需要保存,所以先存,再判断终止条件。
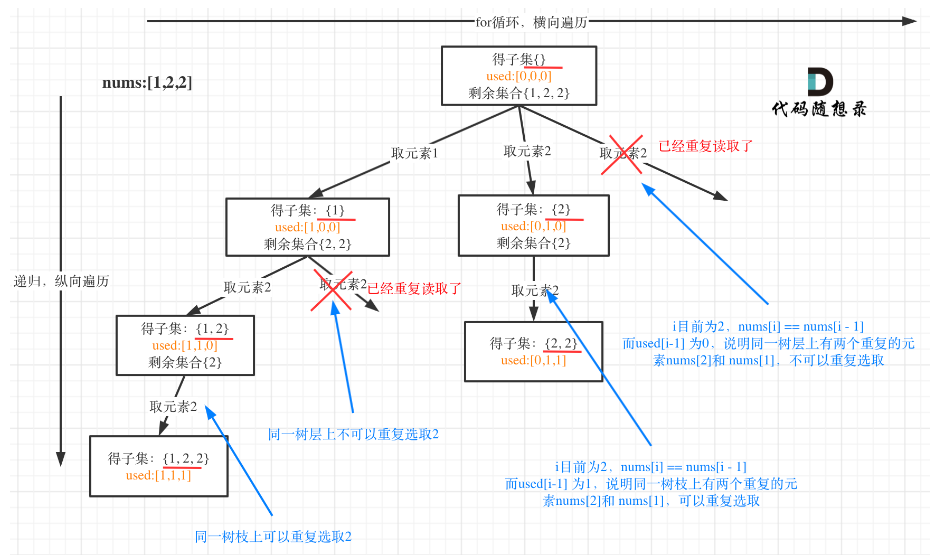
子集II (含有重复元素)
在同一层中不可选取相同元素,属于树层去重。
其实树层去重可以不用used数组,直接排序后判断相邻的数是否相同就可以完成树层去重。
注意:去重都需要排序!!!
递增子序列
需要解决的问题:
去重问题,仍然是树层的去重,但是不能对数组进行排序了,于是用哈希表进行去重;
选取的是符合条件的每个节点,其实可以与之前的联系起来,相当于可以不用写终止条件;
排列问题
全排列(没有重复元素)
排列问题就不需要startIndex了,需要使用used数组,来确定该数字在path中已经被取过了。
全排列II(有重复元素)
使用used数组+哈希表进行树枝去重和数层去重。