回溯算法刷题总结
- 回溯法理论基础
- 回溯算法的模板
- 组合问题
- 77.组合
- 优化版本
- 216.组合总和III
- 17.电话号码的字母组合
- 组合总和
- 组合总和II
- 分割
- 131.分割回文串
- 93.复原IP地址
- 子集
- 78.子集
- 90.子集II
- 491.递增子序列(和子集问题很像)
- 排列
- 全排列
- 全排列II
- 其他问题
- 332.重新安排行程(深搜和回溯相辅相成)
回溯法理论基础
回溯法一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独问题
回溯算法的模板
void backtracking(参数){
if(终止条件){
存放结果;
return;
}
for(选择:本层集合中元素(树中节点孩子的数量就是集合的大小)){
处理节点;
backtracking(路径,选择列表); //递归
回溯,撤销处理结果;
}
}
组合问题
77.组合
力扣题目链接
将结果集ans和路径集path设置为全局变量
class Solution {
public:
vector<vector<int> > ans;
vector<int> path;
void backtracking(int n,int k,int starttIndex){
if(path.size()==k){
ans.push_back(path);
return;
}
for(int i =starttIndex;i<=n;i++)
{
path.push_back(i);
backtracking(n,k,i+1);
path.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(n,k,1);
return ans;
}
};
优化版本
class Solution {
public:
vector<vector<int> > result;
vector<int> path;
void backtracking(int startindex,int n,int k)
{
if(path.size()==k){
result.push_back(path);
return;
}
for(int i=startindex;i<=n-(k-path.size())+1;i++){
path.push_back(i);
backtracking(i+1,n,k);
path.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(1,n,k);
return result;
}
};
216.组合总和III
class Solution {
public:
vector<vector<int> > result;
vector<int> path;
void backtracking(int startindex,int k,int n)
{
if(path.size()==k)
{
int sum=0;
for(int i =0;i<k;i++){
sum+=path[i];
}
if(sum==n){
result.push_back(path);
}
return;
}
for(int i=startindex;i<=9-(k-path.size())+1;i++){
path.push_back(i);
backtracking(i+1,k,n);
path.pop_back();
}
}
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(1,k,n);
return result;
}
};
17.电话号码的字母组合
class Solution {
public:
string str[10]={" "," ","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> result;
string path="";
void backtracking(int n,string digits)
{
if(path.length()==digits.length())
{
result.push_back(path);
return;
}
int num = digits[n]-'0';
for(int i=0;i<str[num].length();i++)
{
path+=str[num][i]; //处理节点
backtracking(n+1,digits); //
path=path.substr(0,path.length()-1); //回溯,撤销
}
}
vector<string> letterCombinations(string digits) {
if (digits.length()==0){
return result;
}
else{
backtracking(0,digits);
return result;
}
}
};
组合总和
class Solution {
public:
vector<vector<int> > result;
vector<int> path;
void backtracking(int startindex,int sum,int target,vector<int>& candidates)
{
if(sum>=target){
if(sum==target){
result.push_back(path);
}
return ;
}
for(int i=startindex;i<candidates.size();i++){
sum+=candidates[i];
path.push_back(candidates[i]);
backtracking(i,sum,target,candidates);
sum-=candidates[i];
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
backtracking(0,0,target,candidates);
return result;
}
};
组合总和II
这道题考察的是“回溯算法中的去重,树层去重or树枝去重"。根据题意,要求元素在同一个组合内可以重复,但是两个组合不能相同。所以我们要去重的是同一数层上使用过,同一树枝上不用去重。
- 树层去重首先需要对数组进行排序
- 树层去重中使用了一个trick,加入了used数组(bool 类型),表示该数在同一树层或同一树枝中是否被使用过
used[i-1]=true,说明同一树枝candidates[i-1]使用过
used[i-1]=false,说明同一树层candidates[i-1]使用过
class Solution {
public:
vector<vector<int> > result;
vector<int> path;
void backtracking(int startindex, int sum, int target, vector<int>& candidates, vector<bool>& used)
{
if(sum==target){
result.push_back(path);
return;
}
for(int i=startindex;i<candidates.size()&&sum+candidates[i]<=target;i++){
if(i>0&&candidates[i]==candidates[i-1]&&used[i-1]==false) continue; //注意i>0
sum+=candidates[i];
path.push_back(candidates[i]);
used[i]=true;
backtracking(i+1,sum,target,candidates,used);
used[i]=false;
path.pop_back();
sum-=candidates[i];
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<bool> used(candidates.size(),false);
sort(candidates.begin(),candidates.end());
backtracking(0,0,target,candidates,used);
return result;
}
};
分割
131.分割回文串
使用回溯法分割回文串的精髓在于切割线的确定
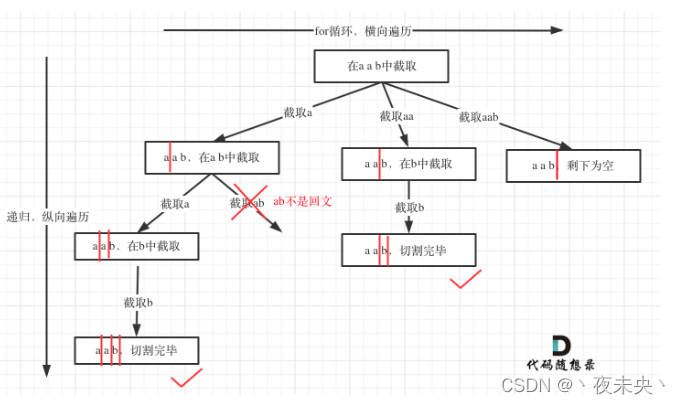
在每一层遍历的时候,startindex到 i 之间的子串即可被用来去判定是否是回文串,如果是则更新切割线位置,进入下一层枝干,如果不是继续 i+1更新切割线位置。
class Solution {
public:
vector<vector<string> > res;
vector<string> path;
bool isPalindrome(string& str, int start, int end){
for(int i =start,j=end;i<j;i++,j--){
if(str[i]!=str[j]){
return false;
}
}
return true;
}
void backtracking(string& str, int startindex){
if(startindex>=str.size()){
res.push_back(path);
return;
}
for(int i =startindex;i<str.size();i++){
if(isPalindrome(str,startindex,i)){
path.push_back(str.substr(startindex,i-startindex+1));
backtracking(str,i+1);
path.pop_back();
}
else continue;
}
}
vector<vector<string>> partition(string s) {
backtracking(s,0);
return res;
}
};
93.复原IP地址
这里在判断isIP时候卡了一下,用了std::stoi函数,对于不能百分之百确定string转成int的,建议用s[i] - ‘0’一个一个转换。
class Solution {
public:
vector<string> res;
vector<string> path;
bool isIP(string& s, int start, int end) {
if(start>end||s[start]=='0'&&start!=end) return false;
int num = 0;
for(int i =start;i<=end;i++){
if(s[i]>'9'||s[i]<'0') return false;
num = num*10+(s[i]-'0');
if(num>255) return false;
}
return true;
}
void backtracking(string& s, int startindex) {
if (path.size() >= 4) {
if (path.size() == 4 && startindex == s.size()) {
string ans = "";
for (auto p : path) ans = ans + p + ".";
ans = ans.substr(0, ans.size() - 1);
res.push_back(ans);
}
return;
}
for (int i = startindex; i < s.size(); i++) {
if (isIP(s, startindex, i)) {
path.push_back(s.substr(startindex, i - startindex + 1));
backtracking(s, i + 1);
path.pop_back();
}
else continue;
}
}
vector<string> restoreIpAddresses(string s) {
backtracking(s, 0);
return res;
}
};
子集
78.子集
如果把子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点,子集问题也是一种组合问题,因为它的集合是无序的。
class Solution {
public:
vector<vector<int> > res;
vector<int> path;
void backtracking(vector<int>& nums,int startindex){
if(startindex>=nums.size()){
res.push_back(path);
return;
}
res.push_back(path); // 子集问题由于是找所有节点,所以每次res每次都要存值
for(int i = startindex;i<nums.size();i++){
path.push_back(nums[i]);
backtracking(nums,i+1);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
backtracking(nums,0);
return res;
}
};
90.子集II
数组里包含有重复元素,而返回的解集却不能包含重复元素,这让我想起了树层去重,先试一下使用used数组。ac掉了,说明这道题就是树层去重
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backtracking(vector<int>& nums, vector<bool>& used, int startindex){
if(startindex>=nums.size()){
res.push_back(path);
return;
}
res.push_back(path);
for(int i=startindex;i<nums.size();i++){
if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false){
continue;
}
used[i]=true;
path.push_back(nums[i]);
backtracking(nums, used, i+1);
path.pop_back();
used[i]=false;
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
vector<bool> used(nums.size(),false);
sort(nums.begin(),nums.end());
backtracking(nums,used,0);
return res;
}
};
491.递增子序列(和子集问题很像)
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backtracking(vector<int>& nums, int startindex){
if(path.size()>1){
res.push_back(path);
}
unordered_set<int> uset;
for(int i =startindex;i<nums.size();i++){
if((!path.empty()&&nums[i]<path.back())||uset.find(nums[i])!=uset.end()) continue;
uset.insert(nums[i]);
path.push_back(nums[i]);
backtracking(nums,i+1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
backtracking(nums,0);
return res;
}
};
排列
全排列
有组合问题改成排列问题需要注意两点,第一点是不需要startindex,第二点是需要使用一个used数组来记录元素是否被使用过
class Solution {
public:
vector<vector<int> > res;
vector<int> path;
void backtracking(vector<int>& nums,vector<bool>& used){
if(path.size()==nums.size()){
res.push_back(path);
return;
}
for(int i =0;i<nums.size();i++){
if(used[i]!=true){
path.push_back(nums[i]);
used[i] = true;
backtracking(nums,used);
used[i] = false;
path.pop_back();
}
else continue;
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<bool> used(nums.size(),false);
backtracking(nums,used);
return res;
}
};
全排列II
class Solution {
public:
vector<vector<int> > res;
vector<int> path;
void backtracking(vector<int>& nums,vector<bool> used)
{
if(path.size()==nums.size()){
res.push_back(path);
return;
}
for(int i =0;i<nums.size();i++){
if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false){
continue;
}
if(used[i]==false){
path.push_back(nums[i]);
used[i] = true;
backtracking(nums,used);
used[i] = false;
path.pop_back();
}
}
}
vector<vector<int> > permuteUnique(vector<int>& nums) {
vector<bool> used(nums.size(), false);
sort(nums.begin(),nums.end());
backtracking(nums,used);
return res;
}
};
其他问题
332.重新安排行程(深搜和回溯相辅相成)
class Solution {
public:
unordered_map<string,map<string,int>> target;
vector<string> res;
bool backtracking(vector<vector<string>>& tickets){
if(res.size()==tickets.size()+1){
return true;
}
for(auto &tar:target[res[res.size()-1]]){
if(tar.second>0){
res.push_back(tar.first);
tar.second--;
if(backtracking(tickets)) return true;
res.pop_back();
tar.second++;
}
}
return false;
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
for(auto ticket:tickets){
target[ticket[0]][ticket[1]]++;
}
res.push_back("JFK");
backtracking(tickets);
return res;
}
};