62. 不同路径

一个机器人位于一个 $m\ast n$ 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

实例 1：

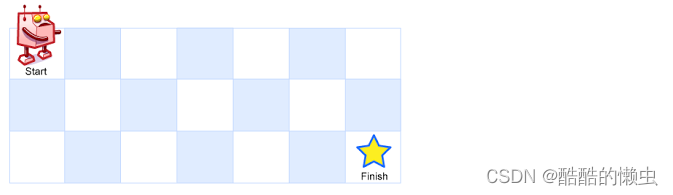
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 $2\ast 10^9$

思路：(动态规划)

由于每次只能向下或者向右移动，所以到达任意一个位置，不是从上面到达就是从左边到达，从而到达该位置的路径就是这两个方向之和：

• 定义一个 m*n 矩阵dp，用于存放到达当前位置的所有路径；
• 第一列和第一行比较特殊，分别只能从上方到达，从左面到达，因此只用一条路，赋值为1；
• 其余位置要比较从左面，从上面到达，所以动态方程为：dp[i][j] = dp[i-1][j] + dp[i][j-1]

代码：(Java)

public class difPath {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int m = 3, n = 7; 
		System.out.println(uniquePaths(m, n));
		
	}
	public static int uniquePaths(int m, int n) {
		int [][] dp = new int[m][n];
		for(int i = 0; i < m; i++) {
			dp[i][0] = 1;
		}
		for(int j = 0; j < n; j++) {
			dp[0][j] = 1;
		}
		for(int i = 1; i < m; i++) {
			for (int j = 1; j < n; j++) {
				dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
			}
		}
		return dp[m-1][n-1];
	}
}

运行结果：

复杂度分析：

时间复杂度：O(m∗n) 。
空间复杂度：O(m∗n) 。（优化：因为我们每次只需要 dp[i-1][j],dp[i][j-1]，所以我们只要记录这两个数，所以空间复杂度可以为 ：O(1) . ）

注：仅供学习参考！

题目来源：力扣。