子数组达到规定累加和的最大长度系列问题

news2024/12/26 0:11:27

文章目录

1、题目一：正整数数组中子数组累加和 = K K K 最大长度

1.1 题目描述

给定一个 正整数 组成的无序数组 arr，给定一个 正整数值 K。

找到 arr 的所有子数组里，哪个子数组的累加和等于K，并且是长度最大的，返回其长度。

例子：

arr = [3, 2, 1, 3, 3, 1, 1, 1, 1, 1, 1, 2, 2, 2]，K = 6

累加和为6的子数组：
1. [3, 2, 1]
2. [2, 1, 3]
3. [3, 3]
4. [1, 1, 1, 1, 1, 1]
5. [2, 2, 2]
6. .....

最大长度为6，[1, 1, 1, 1, 1, 1] 这个子数组

1.2 思路分析

子数组是连续的。

本题利用了窗口单调性的构造。

仍然以题目给定的例子进行流程讲解。

假设是非负数组，构造一个窗口，一开始在数组的左侧，则 L < 0 且 R < 0，窗口内没有一个数，此时窗口内的累加和 Sum 为0。

1）若 Sum < K，则 R++；
2）若 Sum = K，收集答案，即窗口内的数字数量，然后 R++；之所以 R++，因为后面有可能跟着0，使得这个子数组长度更长。
3）若 Sum > K，则L++。

当Sum < K时，R++，就是在找以数组的 L 位置为开头累加和等于 K 的情况；

当Sum > K时，L++，就是在更换数组的开头位置，换下一个位置为开头找累加和等于 K 的的情况。

这个流程之所以对，是因为找到了以每个位置为开头满足条件的所有情况。

之所以窗口可以这样滑动是因为这是个非负数组，所以具有单调性，范围变大，累加和不可能变小；而窗口变小，累加和只可能变小或者相等。

窗口能解决的问题一定都存在某个范围对应指标的单调性，本题的指标就是累加和。

1.3 代码实现

public class LongestSumSubArrayLengthInPositiveArray {

	public static int getMaxLength(int[] arr, int K) {
		if (arr == null || arr.length == 0 || K <= 0) {
			return 0;
		}
		int left = 0;
		int right = 0;
		int sum = arr[0];
		int len = 0;
		while (right < arr.length) {
			//正数数组，相等的情况下，无论先让L还是R动，另一个都会紧跟着移动的
			//但是如果是非负数组，相等的情况下，让R++，因为下一个位置可能是0，使得长度更长
			if (sum == K) { 
				len = Math.max(len, right - left + 1);
				sum -= arr[left++]; 
			} else if (sum < K) {
				right++;
				if (right == arr.length) {
					break;
				}
				sum += arr[right];
			} else {
				sum -= arr[left++];
			}
		}
		return len;
	}
}

对数器：

public class LongestSumSubArrayLengthInPositiveArray {
	// for test
	public static int right(int[] arr, int K) {
		int max = 0;
		for (int i = 0; i < arr.length; i++) {
			for (int j = i; j < arr.length; j++) {
				if (valid(arr, i, j, K)) {
					max = Math.max(max, j - i + 1);
				}
			}
		}
		return max;
	}

	// for test
	public static boolean valid(int[] arr, int L, int R, int K) {
		int sum = 0;
		for (int i = L; i <= R; i++) {
			sum += arr[i];
		}
		return sum == K;
	}

	// for test
	public static int[] generatePositiveArray(int size, int value) {
		int[] ans = new int[size];
		for (int i = 0; i != size; i++) {
			ans[i] = (int) (Math.random() * value) + 1;
		}
		return ans;
	}

	// for test
	public static void printArray(int[] arr) {
		for (int i = 0; i != arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int len = 50;
		int value = 100;
		int testTime = 500000;
		System.out.println("test begin");
		for (int i = 0; i < testTime; i++) {
			int[] arr = generatePositiveArray(len, value);
			int K = (int) (Math.random() * value) + 1;
			int ans1 = getMaxLength(arr, K);
			int ans2 = right(arr, K);
			if (ans1 != ans2) {
				System.out.println("Oops!");
				printArray(arr);
				System.out.println("K : " + K);
				System.out.println(ans1);
				System.out.println(ans2);
				break;
			}
		}
		System.out.println("test end");
	}
}

2、题目二：整数数组中子数组累加和为 = K K K 的最大长度

2.1 题目描述

给定一个 整数 组成的无序数组 arr，值可能正、可能负、可能0。给定一个 整数值 K。

找到 arr 的所有子数组里，哪个子数组的累加和等于K，并且是长度最大的，返回其长度。

2.2 思路分析

本题不能使用窗口了，因为没有单调性了，数组长度变大，并不一定导致累加和不变或者变大，同样地，数组长度变小，并不一定导致累加和变小。就是没有单调性就不能使用窗口。

子数组通常的确定的流程就两种：①必须以每个位置为开头情况是怎样；②必须以每个位置为结尾情况是怎样。

本题将流程定成"以每个位置为结尾的情况下答案是啥"。

将整个大流程拆分为：

  1. 必须以 0 结尾的情况下，哪个累加和为 K K K 的子数组最长。意味着从0位置往左推，推出来的那个子数组能够使得累加和为 K K K 且最长。
  2. 必须以 1 结尾的情况下，哪个累加和为 K K K 的子数组最长。
  3. …

只要能得到任意 i i i 位置结尾情况下推出来的最长结果，那么全局最长的结果就是求的每个位置结果的最大值。

那么对于以任意 i i i 位置结尾的累加和为 K K K 的最长子数组怎么推呢？

假设要求以 100 位置为结尾的累加和为 K = 30 K = 30 K=30 的子数组最长长度，如果已知 0 ~ 100 的累加和为 200，如果 0 ~ 17 的累加和为 170，那么必然知道 18 ~ 100 的累加和为 30。所以找以 100 位置为结尾的累加和为30的子数组最长长度，本质就是在找哪个前缀和是最早出现 170 的。

举例说明具体解法：

请添加图片描述请添加图片描述

2.3 代码实现

import java.util.HashMap;

public class LongestSumSubArrayLength {

	public static int maxLength(int[] arr, int k) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		// key:前缀和
		// value : 0~value这个前缀和是最早出现key这个值的
		HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();
		map.put(0, -1); // important
		int len = 0;
		int sum = 0;
		for (int i = 0; i < arr.length; i++) {
			sum += arr[i];
			if (map.containsKey(sum - k)) {
				len = Math.max(i - map.get(sum - k), len);
			}
			if (!map.containsKey(sum)) {
				map.put(sum, i);
			}
		}
		return len;
	}
}

对数器：

public class LongestSumSubArrayLength {
	// for test
	public static int right(int[] arr, int K) {
		int max = 0;
		for (int i = 0; i < arr.length; i++) {
			for (int j = i; j < arr.length; j++) {
				if (valid(arr, i, j, K)) {
					max = Math.max(max, j - i + 1);
				}
			}
		}
		return max;
	}

	// for test
	public static boolean valid(int[] arr, int L, int R, int K) {
		int sum = 0;
		for (int i = L; i <= R; i++) {
			sum += arr[i];
		}
		return sum == K;
	}

	// for test
	public static int[] generateRandomArray(int size, int value) {
		int[] ans = new int[(int) (Math.random() * size) + 1];
		for (int i = 0; i < ans.length; i++) {
			ans[i] = (int) (Math.random() * value) - (int) (Math.random() * value);
		}
		return ans;
	}

	// for test
	public static void printArray(int[] arr) {
		for (int i = 0; i != arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	public static void main(String[] args) {
		int len = 50;
		int value = 100;
		int testTime = 500000;

		System.out.println("test begin");
		for (int i = 0; i < testTime; i++) {
			int[] arr = generateRandomArray(len, value);
			int K = (int) (Math.random() * value) - (int) (Math.random() * value);
			int ans1 = maxLength(arr, K);
			int ans2 = right(arr, K);
			if (ans1 != ans2) {
				System.out.println("Oops!");
				printArray(arr);
				System.out.println("K : " + K);
				System.out.println(ans1);
				System.out.println(ans2);
				break;
			}
		}
		System.out.println("test end");
	}
}

2.4 引申变形

题目：给定一个整数数组，有正、有负还有0，找到数组的所有子数组，哪个子数组-1的数量和1的数量相同，并且长度是最大的，返回其长度。

思路：将数组进行处理：所有 非-1和 非1 的无关数全部变成0。这题本质就是在求累加和为 0 的子数组的最长长度，处理后的数组累加和为 0 的子数组就是 -1 和 1 的数量一样多。

2.5 技巧应用题

2.5.1 剑指 Offer II 010. 和为 k 的子数组数量

原题地址：剑指 Offer II 010. 和为 k 的子数组
相同题目： Leetcode 560. 和为 K 的子数组

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        //前缀和 + 哈希表

        //key为前缀和，value为该前缀和出现的次数
        unordered_map<int, int> mp;
        mp[0] = 1;
        int sum = 0; //前缀和
        int cnt = 0;
		
		//以 i 位置结尾的子数组和为k的个数
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];

            if (mp.count(sum - k)) {//判断前缀和sum-k是否出现过
                cnt += mp[sum - k];
            } 
            if (!mp.count(sum)) {
                mp[sum] = 1;
            } else {
                mp[sum]++;
            }
        }

        return cnt;
    }
};

2.5.2 剑指 Offer II 011. 0 和 1 个数相同的子数组

原题地址：剑指 Offer II 011. 0 和 1 个数相同的子数组
相同题目： Leetcode 525. 连续数组

题目：给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

思路：由于「0 和 1 的数量相同」等价于「1的数量减去 0的数量等于 0」，可以将数组中的 0 视作 −1，则原问题转换成「求最长的连续子数组，其元素和为0」

代码：

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
		//前缀和+哈希表
		
        //由于「0和 1 的数量相同」等价于「1的数量减去 0 的数量等于 0」，
        //可以将数组中的 0 视作 −1，则原问题转换成「求最长的连续子数组，其元素和为0」

        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] == 0) {
                nums[i] = -1;
            }
        }

        // 以 i 位置结尾的子数组累加和为0
        int sum = 0;
        int len = 0;
        
        //key为前缀和，value为该前缀和第一次出现的位置
        unordered_map<int, int> mp;
        mp[0] = -1; //important

        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];

            if (mp.count(sum)) {
                len = max(len, i - mp[sum]);
            }

            if (!mp.count(sum)) {
                mp[sum] = i; //记录该累加和最早出现的位置
            }
        }
        return len;
    }
};

3、题目三：整数数组中子数组累加和 ≤ K \le K ≤K 的最大长度

3.1 题目描述

给定一个整数组成的无序数组 arr，值可能正、可能负、可能0，给定一个整数值 K。

找到 arr 的所有子数组里，哪个子数组的累加和 ≤ K \le K ≤K，并且是长度最大的，返回其长度。

3.2 思路分析

本题可用 O ( N ) O(N) O(N) 复杂度解决，即是最优解。

举例说明流程：假设一个数组 arr = [1, 2, -4, 3, 7, -2, 4, -3]

准备两个数组： minSum 和 minSumEnd，均与 arr 等长。

从后往前遍历数组arr，其中 minSum[i] 表示如果子数组必须以 i 开头，子数组能够取得最小的累加和，而 minSumEnd[i] 表示必须以 i 开头的子数组取得最小累加和的时候的右边界。

请添加图片描述
注意：5位置如果往右扩，就只用看它后面的1个位置的最小累加和，因为如果往右扩必然把6位置包含，而 minSum 中 6 位置存储的已经是从6位置开始子数组累加和最小的值，是可以直接使用的，而5本身是个负数，如果往右扩就发现无利可图，所以不再往右扩。

也就是说对于每个位置为开头，它的子数组都有两种选择：① 仅自己；②往右扩。而是否选择往右扩就只看它的后一个位置的最小累加和，若为非正数则有利可图，可以往右扩；否则无利可图，放弃往右扩的选择。

minSum 和 minSumEnd 这两个数组很厉害，任意以 i 位置开头的子数组的所有情况中最优的、最小的累加和存在 minSum 中，最优的、最小的累加和到达的右边界存在 minSumEnd 中，都是以 i 开头的所有情况中的最好。

因为要求的是 i 开头的情况下往右扩的位置，所以是 i 位置的信息依赖于 i+1 位置，i+1 位置的信息就要比 i 位置先算，因此从右往左遍历。 而如果是以 i 结尾的情况，i 位置信息依赖于 i-1 位置，就要从左往右遍历。从哪边开始计算，是根据依赖顺序决定的。

主流程：使用窗口。

通过 minSum 数组看 0 位置开头的子数组累加和 a a a，如果 a > K a > K a>K，则说明从 0 位置开始的任何子数组累加和都不会 ≤ K \le K ≤K。

但是如果 a ≤ K a \le K a≤K，假设通过 minSumEnd 数组知道 0 位置能扩到的位置是 p p p，则看 p + 1 p+1 p+1 位置开头的最小累加和 b b b，如果 a + b ≤ K a + b \le K a+b≤K，则继续往后看；

假设 p p p 位置能扩到的位置是 q q q，则看 q + 1 q + 1 q+1 位置开头的最小累加和 c c c，如果 a + b + c > K a + b + c > K a+b+c>K，那么就不要 q + 1 q + 1 q+1 开头的这范围。

那么必须以 0 位置开头的累加和 ≤ K \le K ≤K 的最长子数组就是最小累加和为 a a a 和 b b b 这两块区域推导出来的范围，即 [0, q]。

同时，能得到从0开始到 q q q 的累加和 sum，接下来将这个窗口变成 1 到 q q q，则该范围的累加和为 sum - arr[0]，记录为 sum'，然后看 sum' 能否把 q+1 位置为开头的子数组吸纳，即 判断 s u m ′ + c ≤ K sum' + c\le K sum′+c≤K 是否成立。

也就是说在当前已经找到的一个区域中，以下一个位置为开头，看未被吸纳的区域是否能被纳入。
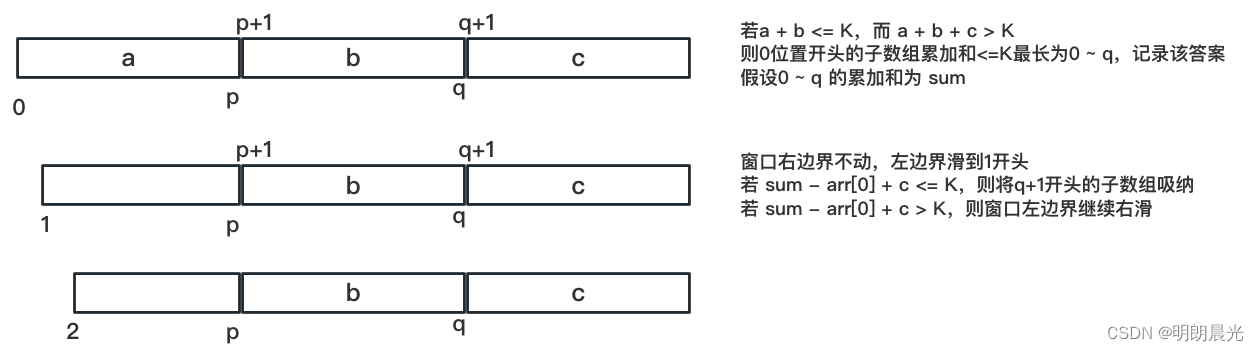
在这里插入图片描述

这个过程中，窗口的右边界没有回退。

这种做法为什么正确呢？

一开始得到从0位置开始的答案，正确性毋庸置疑。但是从 1 位置开始的时候并没有求得它的最长子数组，那么这种做法为什么正确呢？因为假设 1 开始的位置，它的正确答案范围的右边界在 q q q 的左边，那么这个答案我们不关心，因为这个长度一定是小于 0 位置开始得到的长度。所以这个流程里并没有求出以每个位置为开头的准确答案，而是只关心是否能将答案长度推高的可能性。意思就是 0 已经推到 q q q 位置，在 0 退出的情况下， q + 1 q+1 q+1位置开头的子数组能否被吸纳，如果不能被吸纳，更甚者比原先的答案长度还短，那就直接舍弃。2位置同理。

本题的难点就在于某些可能性是要舍弃的。

最优解就是舍弃了某些可能性，原理就是已经找到 L L L 出发到 R R R 的一个解，如果 L + 1 L+1 L+1 开头的答案比之前的答案短，就直接舍弃，因为关心的是全局最长。

整理一下整个流程：

  1. 先利用 minSum 和 minSumEnd 数组将 0 位置开头的累加和 ≤ K \le K ≤K 的子数组最长长度求得，假设是0 ~ 13，长度为 14；
  2. 在 0 位置从窗口中出去的情况下，以1位置为开头，窗口右边界依然在 13，维护 [1, 13] 这个范围的累加和，看14开头的满足条件的子数组能否进入窗口。如果不能进入窗口，则收集一个答案，这个答案可能是1位置开头的累加和 ≤ K \le K ≤K的子数组最长长度，也可能不是，但是无所谓，因为这个长度已经比 14 小了；如果能进入窗口，则继续往右扩；
  3. 在 1 位置从窗口中出去的情况下，维护 [2, 13] 这个范围的累加和，是否能将 14 开头满足条件的子数组吸纳。如果可以，假设14开头扩到了 26，那么收集到了2位置开头的累加和 ≤ K \le K ≤K的子数组最长长度为 25，即[2, 26]。
  4. 极端情况是 [0, 13] 这个窗口每次都无法往后扩，那么当窗口中没有数据的时候，窗口左边界到14 位置，就从 14 位置出发，继续往右扩。

如果暴力地从每个位置开始往右扩，找满足条件的子数组，固然也能解决，但是这种方式的时间复杂度为 O ( N 2 ) O(N^2) O(N2)。

3.3 代码实现

public class LongestLessSumSubArrayLength {
	//最优解：时间复杂度O(N)
	public static int maxLengthAwesome(int[] arr, int k) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int[] minSums = new int[arr.length];
		int[] minSumEnds = new int[arr.length];
		//从右往左遍历填 minSums 和 minSumEnds 数组
		//所以可以确定最后一个位置
		minSums[arr.length - 1] = arr[arr.length - 1];
		minSumEnds[arr.length - 1] = arr.length - 1;
		//从右往左遍历填 minSums 和 minSumEnds 数组
		for (int i = arr.length - 2; i >= 0; i--) {
			if (minSums[i + 1] < 0) {
				minSums[i] = arr[i] + minSums[i + 1];
				minSumEnds[i] = minSumEnds[i + 1];
			} else {
				minSums[i] = arr[i];
				minSumEnds[i] = i;
			}
		}
		
		int end = 0; // 迟迟扩不进来那一块儿的开头位置，不会回退
		int sum = 0; // 窗口累加和
		int ans = 0; //最大长度，就是最终结果
		//因为end是不回退的，所以时间复杂度为O(N)
		for (int i = 0; i < arr.length; i++) { //从0位置开头扩到了哪儿、1位置开头扩到了哪儿、......
			// while循环结束之后：
			// 1) 如果以i开头的情况下，累加和<=k的最长子数组是arr[i..end-1]，看看这个子数组长度能不能更新res；
			// 2) 如果以i开头的情况下，累加和<=k的最长子数组比arr[i..end-1]短，更新还是不更新res都不会影响最终结果；
			while (end < arr.length && sum + minSums[end] <= k) { //迟迟扩不进来的那块可以吸纳
				sum += minSums[end];
				end = minSumEnds[end] + 1; 
			}
			ans = Math.max(ans, end - i); //收集答案，end - i可能是i开头的准确答案，也可能不是。如果不是，长度就较短，本来也比之前的答案小，所以不关心；如果是，那就可能将答案推到更高
			if (end > i) { // 还有窗口，哪怕窗口没有数字 窗口的范围是[i,end) [4,4)
				sum -= arr[i];
			} else { // i == end,  即将 i++, 则 i > end, 此时窗口概念维持不住了，所以end跟着i一起走
				//例子：arr = [-10, 6, 3, 1, 5, -5], K = 0
				//		下标：   0  1  2  3  4  5
				//则窗口[0,3]是0开头的答案，sum = 0，此时end = 4，即 4 位置开头的数组是进不了窗口的
				//0位置的-10出窗口，[1,3] sum = 10 > 0, 4位置开头的数组依然进不了窗口
				//1位置的6出窗口，[2,3] sum = 4 > 0, 4位置开头的数组依然进不了窗口
				//2位置的3出窗口，[3,3] sum = 1 > 0, 4位置开头的数组依然进不了窗口
				//3位置的1出窗口，此时窗口中无数据，且i=3，接下来i++，到了4位置，但是4位置的数不能进窗口，因为4位置的5 > 0，此时的i = end
				//接下来到5位置进行计算，于是end跟着i走，看5位置开头是否能继续往后扩
				end = i + 1;
			}
		}
		return ans;
	}
	
	//对数器方法（次优解）：时间复杂度O(NlogN)
	public static int maxLength(int[] arr, int k) {
		int[] h = new int[arr.length + 1];
		int sum = 0;
		h[0] = sum;
		for (int i = 0; i != arr.length; i++) {
			sum += arr[i];
			h[i + 1] = Math.max(sum, h[i]);
		}
		sum = 0;
		int res = 0;
		int pre = 0;
		int len = 0;
		for (int i = 0; i != arr.length; i++) {
			sum += arr[i];
			pre = getLessIndex(h, sum - k);
			len = pre == -1 ? 0 : i - pre + 1;
			res = Math.max(res, len);
		}
		return res;
	}

	public static int getLessIndex(int[] arr, int num) {
		int low = 0;
		int high = arr.length - 1;
		int mid = 0;
		int res = -1;
		while (low <= high) {
			mid = (low + high) / 2;
			if (arr[mid] >= num) {
				res = mid;
				high = mid - 1;
			} else {
				low = mid + 1;
			}
		}
		return res;
	}

	// for test
	public static int[] generateRandomArray(int len, int maxValue) {
		int[] res = new int[len];
		for (int i = 0; i != res.length; i++) {
			res[i] = (int) (Math.random() * maxValue) - (maxValue / 3);
		}
		return res;
	}

	public static void main(String[] args) {
		System.out.println("test begin");
		for (int i = 0; i < 10000000; i++) {
			int[] arr = generateRandomArray(10, 20);
			int k = (int) (Math.random() * 20) - 5;
			if (maxLengthAwesome(arr, k) != maxLength(arr, k)) {
				System.out.println("Oops!");
			}
		}
		System.out.println("test finish");
	}
}

4、题目四：整数数组中子数组平均值 ≤ v \le v ≤v 的最大长度

4.1 题目描述

给定一个数组arr，给定一个值v。

求子数组平均值 ≤ v \le v ≤v 的最长子数组长度。

4.2 思路分析

首先预处理——将原数组 arr 中的每个值都减去 v v v。

然后求预处理数组中子数组累加和 ≤ 0 \le 0 ≤0 的最大长度。

4.3 代码实现

import java.util.TreeMap;

public class AvgLessEqualValueLongestSubarray {
	// 时间复杂度O(N)
	public static int ways3(int[] arr, int v) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		
		//预处理
		for (int i = 0; i < arr.length; i++) {
			arr[i] -= v; 
		}
		return maxLengthAwesome(arr, 0);
	}

	// 找到数组中累加和<=k的最长子数组
	public static int maxLengthAwesome(int[] arr, int k) {
		int N = arr.length;
		int[] sums = new int[N];
		int[] ends = new int[N];
		sums[N - 1] = arr[N - 1];
		ends[N - 1] = N - 1;
		for (int i = N - 2; i >= 0; i--) {
			if (sums[i + 1] < 0) {
				sums[i] = arr[i] + sums[i + 1];
				ends[i] = ends[i + 1];
			} else {
				sums[i] = arr[i];
				ends[i] = i;
			}
		}
		int end = 0;
		int sum = 0;
		int res = 0;
		for (int i = 0; i < N; i++) {
			while (end < N && sum + sums[end] <= k) {
				sum += sums[end];
				end = ends[end] + 1;
			}
			res = Math.max(res, end - i);
			if (end > i) {
				sum -= arr[i];
			} else {
				end = i + 1;
			}
		}
		return res;
	}
}

对数器：

public class AvgLessEqualValueLongestSubarray {
	// 暴力解，时间复杂度O(N^3)，用于做对数器
	public static int ways1(int[] arr, int v) {
		int ans = 0;
		for (int L = 0; L < arr.length; L++) {
			for (int R = L; R < arr.length; R++) {
				int sum = 0;
				int k = R - L + 1;
				for (int i = L; i <= R; i++) {
					sum += arr[i];
				}
				double avg = (double) sum / (double) k;
				if (avg <= v) {
					ans = Math.max(ans, k);
				}
			}
		}
		return ans;
	}

	// 解法2，时间复杂度O(N*logN)
	public static int ways2(int[] arr, int v) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		TreeMap<Integer, Integer> origins = new TreeMap<>();
		int ans = 0;
		int modify = 0;
		for (int i = 0; i < arr.length; i++) {
			int p1 = arr[i] <= v ? 1 : 0;
			int p2 = 0;
			int querry = -arr[i] - modify;
			if (origins.floorKey(querry) != null) {
				p2 = i - origins.get(origins.floorKey(querry)) + 1;
			}
			ans = Math.max(ans, Math.max(p1, p2));
			int curOrigin = -modify - v;
			if (origins.floorKey(curOrigin) == null) {
				origins.put(curOrigin, i);
			}
			modify += arr[i] - v;
		}
		return ans;
	}

	// 用于测试
	public static int[] randomArray(int maxLen, int maxValue) {
		int len = (int) (Math.random() * maxLen) + 1;
		int[] ans = new int[len];
		for (int i = 0; i < len; i++) {
			ans[i] = (int) (Math.random() * maxValue);
		}
		return ans;
	}

	// 用于测试
	public static int[] copyArray(int[] arr) {
		int[] ans = new int[arr.length];
		for (int i = 0; i < arr.length; i++) {
			ans[i] = arr[i];
		}
		return ans;
	}

	// 用于测试
	public static void printArray(int[] arr) {
		for (int i = 0; i < arr.length; i++) {
			System.out.print(arr[i] + " ");
		}
		System.out.println();
	}

	// 用于测试
	public static void main(String[] args) {
		System.out.println("测试开始");
		int maxLen = 20;
		int maxValue = 100;
		int testTime = 500000;
		for (int i = 0; i < testTime; i++) {
			int[] arr = randomArray(maxLen, maxValue);
			int value = (int) (Math.random() * maxValue);
			int[] arr1 = copyArray(arr);
			int[] arr2 = copyArray(arr);
			int[] arr3 = copyArray(arr);
			int ans1 = ways1(arr1, value);
			int ans2 = ways2(arr2, value);
			int ans3 = ways3(arr3, value);
			if (ans1 != ans2 || ans1 != ans3) {
				System.out.println("测试出错！");
				System.out.print("测试数组：");
				printArray(arr);
				System.out.println("子数组平均值不小于 ：" + value);
				System.out.println("方法1得到的最大长度：" + ans1);
				System.out.println("方法2得到的最大长度：" + ans2);
				System.out.println("方法3得到的最大长度：" + ans3);
				System.out.println("=========================");
			}
		}
		System.out.println("测试结束");
	}
}

5、总结

  1. 题目一主要技巧：利用单调性优化

【补充说明】能够使用窗口滑动的前提是具有单调性，就是当窗口的范围变化时，指标（累加和或者给定的数组中的数的类型等）是否有单调性

  1. 题目二主要技巧：利用预处理结构优化 + 讨论开头结尾

【补充说明】题目二记录了「前缀和最早出现的位置」搞定了遍历的问题，不用再遍历地找符合条件的子数组，根据前缀和最早出现的位置直接定位答案。关于「子数组问题」 通常是将答案定成 「必须以 i i i 位置结尾」或者 「必须以 i i i 位置开头」会怎么样，用这种方式解决。

预处理结构 如 「前缀和」、「线段树」、「Index Tree」等。

讨论「数组问题」往往是讨论开头和结尾

  1. 题目三主要技巧：假设答案法 + 淘汰可能性（很难，以后还会见到）

【补充说明】可能在每个位置求不出正确答案，如题目三中精确求解每个位置开头时的答案就不必要，只关注将最终答案变大的可能性，淘汰掉每次都求正确答案的所有情况，只关注能不能变更大的可能性。这是Max Gap 问题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/384187.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

关于HTTP/3的小知识点

关于HTTP/3的小知识点

客户端用 TCP 发送了三个包&#xff0c;但服务器所在的操作系统只收到了后两个包&#xff0c;第一个包丢了。那么内核里的 TCP 协议栈就只能把已经收到的包暂存起来&#xff0c;“停下”等着客户端重传那个丢失的包&#xff0c;这样就又出现了“队头阻塞”。由于这种“队头阻塞…
阅读更多...
Kubernetes之存储管理（中）

Kubernetes之存储管理（中）

NFS网络存储 emptyDir和hostPath存储&#xff0c;都仅仅是把数据存储在pod所在的节点上&#xff0c;并没有同步到其他节点&#xff0c;如果pod出现问题&#xff0c;通过deployment会产生一个新的pod&#xff0c;如果新的pod不在之前的节点&#xff0c;则会出现问题&#xff0c…
阅读更多...
CV——day81（1） 读论文： 基于自监督一致性学习的驾驶场景交通事故检测（有源码）

CV——day81（1） 读论文： 基于自监督一致性学习的驾驶场景交通事故检测（有源码）

Traffic Accident Detection via Self-Supervised Consistency Learning in Driving Scenarios 基于自监督一致性学习的驾驶场景交通事故检测I. INTRODUCTIONIII. OUR APPROACHA. 帧预测B. 物体位置预测C. 驾驶场景上下文表示(DSCR)D. 协作多任务一致性学习E.交通事故判定IV. E…
阅读更多...
UART串口通信协议

UART串口通信协议

一、协议 1.1 消息格式 串口协议是一种全双工、异步通信协议&#xff0c;不需要同步时钟&#xff0c;数据的发送是一位一位的发送&#xff0c;完整的一帧数据通常由起始位、数据、奇偶校验位和停止位组成 1.2 波特率 为确保正确的收发信息&#xff0c;双方必须设置相同的波…
阅读更多...
火山引擎 DataLeap：揭秘字节跳动数据血缘架构演进之路

火山引擎 DataLeap：揭秘字节跳动数据血缘架构演进之路

更多技术交流、求职机会&#xff0c;欢迎关注字节跳动数据平台微信公众号&#xff0c;回复【1】进入官方交流群 DataLeap 是火山引擎数智平台 VeDI 旗下的大数据研发治理套件产品&#xff0c;帮助用户快速完成数据集成、开发、运维、治理、资产、安全等全套数据中台建设&#x…
阅读更多...
MySQL 中的锁有哪些类型，MySQL 中加锁的原则

MySQL 中的锁有哪些类型，MySQL 中加锁的原则

锁的类型MySQL 找那个根据加锁的范围&#xff0c;大致可以分成全局锁&#xff0c;表级锁和行级锁。全局锁全局锁&#xff0c;就是对整个数据库加锁。加锁flush tables with read lock解锁unlock tables全局锁会让整个库处于只读状态&#xff0c;之后所有的更新操作都会被阻塞&a…
阅读更多...
OB运维 | 连接 kill 中的 session_id

OB运维 | 连接 kill 中的 session_id

作者&#xff1a;姚嵩 外星人… 本文来源&#xff1a;原创投稿 *爱可生开源社区出品&#xff0c;原创内容未经授权不得随意使用&#xff0c;转载请联系小编并注明来源。 背景&#xff1a; 通过 obproxy 连接 OB 后&#xff0c;发现&#xff1a; kill 命令使⽤ show processli…
阅读更多...
如何写出让人看不懂的MATLAB代码？

如何写出让人看不懂的MATLAB代码？

最近呢有不少好奇的伙伴私下问咱这是怎么实现大幅度降低matlab代码可读性。于是咱准备将相关的资源分享给大家&#xff0c;这个工具的根来源于大神thrynae (Rik)公开分享一款名叫minify的小工具图片。 咱也不藏着掖着&#xff0c;其实大家用minify作为关键词检索&#xff0c;不…
阅读更多...
学生成绩管理系统/学生信息管理系统

学生成绩管理系统/学生信息管理系统

文章目录项目介绍一、技术栈二、项目功能介绍三、功能页面展示四、获取代码项目介绍 一、技术栈 编程语言&#xff1a;Java 技术栈&#xff1a;ServletJspJdbcEasyUIjQueryAjax面向接口编程 二、项目功能介绍 用户角色&#xff1a;学生、教师、系统管理员。&#xff1b; 管…
阅读更多...
Nuxt 3.0 全栈开发

Nuxt 3.0 全栈开发

Nuxt 3.0 全栈开发 - 杨村长 - 掘金小册核心知识 工程架构 全栈进阶 项目实战&#xff0c;快速精通 Nuxt3 开发&#xff01;。「Nuxt 3.0 全栈开发」由杨村长撰写&#xff0c;299人购买https://s.juejin.cn/ds/S6p7MVo/ 这门课我会全面讲解 Nuxt3 核心知识&#xff0c;然后…
阅读更多...
【uni-app教程】一、UniAPP 介绍

【uni-app教程】一、UniAPP 介绍

一、UniAPP 介绍 (1) 什么是 UniAPP? uni-app 是一个使用 Vue.js 开发所有前端应用的框架&#xff0c;开发者编写一套代码&#xff0c;可发布到 iOS&#xff0c;Android&#xff0c;HS&#xff0c;以及各种小程序&#xff08;微信/支付宝/百度/头条/QQ/钉钉》等多个平台&#…
阅读更多...
Docker之部署Canal

Docker之部署Canal

Canal 就是一个同步增量数据的一个工具。 目录概念Mysql开启binlog是否开启binlog开启binlog日志创建授权用户部署Canal拉取镜像挂载properties配置文件创建容器概念 canal是阿里巴巴旗下的一款开源项目&#xff0c;纯Java开发。基于数据库增量日志解析&#xff0c;提供增量数…
阅读更多...
VTK例子--使用不同的vtkActor同时显示灰度图、体渲染、多边形

VTK例子--使用不同的vtkActor同时显示灰度图、体渲染、多边形

在实际项目中&#xff0c;常遇到不同类型的数据在同一个渲染窗口显示&#xff1b;如网格多边形与灰度图像的显示、体渲染与多边形的显示、体渲染与灰度图像的显示&#xff0c;如下面几张图的效果&#xff1b;多边形灰度图像体渲染多边形体渲染灰度图像如何实现这种混合显示的效…
阅读更多...
怎么连接同局域网下的其他同事的mysql

怎么连接同局域网下的其他同事的mysql

**一、双击运行MySQL 5.5 Command Line Client。**然后输入你这个设备的MySQL的root账户密码 二、输入grant all privileges on *.* to root% identified by"root";&#xff08;identified by后面的是别人要登入的密码&#xff09;后回车。这样就设置局域网内所有ip都…
阅读更多...
【NLP相关】NLP的发展历程

【NLP相关】NLP的发展历程

❤️觉得内容不错的话&#xff0c;欢迎点赞收藏加关注&#x1f60a;&#x1f60a;&#x1f60a;&#xff0c;后续会继续输入更多优质内容❤️&#x1f449;有问题欢迎大家加关注私戳或者评论&#xff08;包括但不限于NLP算法相关&#xff0c;linux学习相关&#xff0c;读研读博…
阅读更多...
C++实现AVL树

C++实现AVL树

目录 一、搜索二叉树 1.1 搜索二叉树概念 二、模拟实现二叉搜索树 2.1 框架 2.2 构造函数 2.2.1 构造函数 2.2.2 拷贝构造 2.2.3 赋值拷贝 2.3 插入函数 2.3.1 insert() 2.3.2 RcInsert() 递归实现 2.4 删除结点函数 2.4.1 Erase() 2.4.2 RcErase() 2.5 中序遍历…
阅读更多...
Nuxt 3.0 全栈开发:五种数据获取 API 选择和应用最佳实践

Nuxt 3.0 全栈开发:五种数据获取 API 选择和应用最佳实践

Nuxt 3.0 全栈开发 - 杨村长 - 掘金小册核心知识 工程架构 全栈进阶 项目实战&#xff0c;快速精通 Nuxt3 开发&#xff01;。「Nuxt 3.0 全栈开发」由杨村长撰写&#xff0c;299人购买https://s.juejin.cn/ds/S6p7MVo/ 上一讲我们学习了如何基于 API Route 编写接口&#…
阅读更多...
12.2 基于Django的服务器信息查看应用（CPU信息）

12.2 基于Django的服务器信息查看应用（CPU信息）

文章目录CPU信息展示图表展示-视图函数设计图表展示-前端界面设计折线图和饼图展示饼图测试折线图celery和Django配合实现定时任务Windows安装redis根据数据库中的数据绘制CPU折线图CPU信息展示 图表展示-视图函数设计 host/views.py def cpu(request):logical_core_num ps…
阅读更多...
【Unity VR开发】结合VRTK4.0：创建人工按钮

【Unity VR开发】结合VRTK4.0：创建人工按钮

语录&#xff1a; 人生需要准备的&#xff0c;不是昂贵的茶&#xff0c;而是喝茶的心情。 前言&#xff1a; 按钮按下抬起是虚仿中经常会出现的功能&#xff0c;那么如何去表现呢&#xff0c;我们可以使用线性变换驱动器对人工按钮进行装箱&#xff0c;以对来自交互器的碰撞做…
阅读更多...
Netty——心跳机制与断线重连

Netty——心跳机制与断线重连

心跳机制与断线重连心跳机制IdleStateHandler客户端服务端测试正常情况异常情况总结断线重连为了保证系统的稳定性&#xff0c;心跳机制和断线重连可是必不可少的&#xff0c;而这两个在Netty中也是非常好实现的心跳机制 我们以客户端发送心跳为例&#xff0c;平时我们的心跳实…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023