学习视频
1.特殊矩阵
1.1 通用特殊矩阵
format
% 零矩阵(全0) 幺矩阵(全1) 单位矩阵
% zeros ones eye rand(生成0~1的随机元素) randn(生成均值为1,方差为0的符合正太分布的随机阵)
zeros(3) % 3x3的全0方阵
zeros(3, 4) % 3x4的全0矩阵
exA = ones(3, 5) % 3x5的全1矩阵
zeros(size(exA)) % 和exA大小一致的全0矩阵
eye(3, 3), eye(5, 3) % 主对角线为1的全0矩阵

示例:


1.2 用于特殊领域的矩阵
魔方矩阵(magic)

范德蒙矩阵(vander)

希尔伯特矩阵(hilb)

2. 矩阵变换
2.1 基础概念
对角阵(diag)
主对角线有值,其他均为0的矩阵
diag作用1 - 创建对角阵:


diag作用2 - 取对角线:

数量矩阵(k*eye)
只有主对角线有值,且全相同

单位矩阵(eye)
只有主对角线有值,且全是1

三角阵

秩(rank)
非零子式的最高阶数就是秩
设在矩阵 A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在的话)全等于0,那么D称为矩阵A的最高阶非零子式,数r称为矩阵A的秩,记作R(A).并规定零矩阵的秩等于0.
-是否可逆: 只有满秩的矩阵才可逆
- 初等变换后矩阵的秩不变
-判断非齐次线性方程组(方程组右侧的值不全为0)解的情况

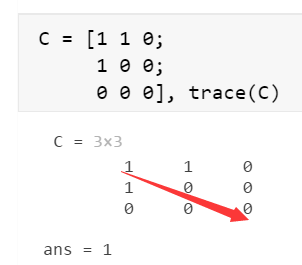
迹(trace)
矩阵主对角线元素的和,trace()计算;相似变换时矩阵的迹不变
逆(inv)和广义逆(pinv)
设A是数域上的一个n阶方阵,若在相同数域上存在另一个n阶矩B,使得:
AB=BA=I
则我们称B是A的逆矩阵,而A则被称为可逆矩阵。

示例:

伪逆:对于非方阵、奇异阵(是方阵,但是行列式为0)、非满秩矩阵(rank(A) ~= n)是不存在逆矩阵的;但是可以去定义一个伪逆矩阵pinv()。

行列式
矩阵行列式是指矩阵的全部元素构成的行列式。排成 n 阶方阵形式的 n^2 个数所确定的一个数称为 n 阶方阵 A 的行列式,记为:det(A) 或 |A|
一个 2x2 的矩阵的行列式可表示为:

范数(norm)
简单来说,用来度量某个向量空间(或矩阵)中的每个向量的长度或大小。
条件数(cond)
矩阵A的条件数等于A的范数与A的逆的范数的乘积,即cond(A)=‖A‖·‖A^(-1)‖,是判断矩阵病态与否的一种度量,条件数越大矩阵越病态。(条件数同时描述了矩阵 A 对向量的拉伸能力和压缩能力,换句话说,令向量发生形变的能力。条件数越大,向量在变换后越可能变化得越多。)
示例:

2.2 矩阵的转置与旋转
转置(.')

共轭转置(')

旋转(rot90(A, k))

左右翻转(fliplr)

上下翻转(flipud)

3.矩阵求值
3.1行列式求值(det)

3.2 矩阵的秩与迹

3.3向量和矩阵的范数


3.4 矩阵的条件数

4.矩阵特征值与特征向量(eig)


5.稀疏矩阵
5.1区分稀疏矩阵(含极大量0元素的矩阵) 和 采用稀疏方式存储的矩阵

5.2稀疏存储方式的产生(sparse)

5.3与稀疏矩阵操作相关的函数
find()

full()

spconvert()

spdiags()

5.4稀疏矩阵应用实例