递增子序列
题目详细:LeetCode.491
注意这道题求的是子序列,而不是子数组,子数组要求其数组是原数组的子集,且元素是连续的,而子序列只需要保证至少有两个元素即可,不需要关系元素是否连续。
所以一开始我确定了递归的结束条件是 startIndex == nums.length 之后,在循环过程中增加了nums[i] - nums[i - 1] < 0 来判断序列是否递增,如果递增则直接break,这样的做法是错误的,因为我们要求的是所有的可能的子序列,所以不能够直接跳出循环,还需要取后续树上的节点。
同时nums[i] - nums[i - 1] < 0 ,判断的是在原数组中连续的元素是否递增,但是子序列并不要求元素是连续的,所以这一判断条件本身也是错的,应该改为nums[i] < path.getLast(),用当前数值来比较上一个递增序列的尾数来判断是否是递增子序列。
在求子序列的同时,还要注意去重,一开始由于收到前面练习题的启发,我利用布尔数组used来进行去重,但发现在这道题中并不适用,因为之前利用used去重,都需要先将原数组进行排序;但在这道题中,排序之后,就得不到与原数组一样的递增子序列,变成从头到尾分割递增序例了,这是互相矛盾的。
所以正确的去重方式,应该是在每一层循环中都新建一个哈希表,用于记录在树形结构的同一层中(循环过程中)已经出现过的数字,假如该数值已经被添加到某一个子序列中,那么后面则不能再添加到该序列中,否则会出现重复的子序列。
这里我们在每一次递归中都新建一个哈希Set来记录在本次循环中出现过的数字,如果出现过,则跳过该数字,继续往后寻找递增的数字组成递增子序列。
以上仅是我的解题思考过程,以及踩过的一些坑和后续看完题解后,对思路的纠正过程,详细的题解可查阅:《代码随想录》— 递增子序列
Java解法(递归,回溯):
class Solution {
List<List<Integer>> ans = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
public void backTrack(int[] nums, int startIndex){
if(path.size() > 1){
ans.add(new ArrayList<>(path));
}
if(startIndex == nums.length){
return;
}
Set<Integer> set = new HashSet<>();
for(int i = startIndex; i < nums.length; i++){
if((!path.isEmpty() && nums[i] < path.getLast()) || set.contains(nums[i])){
continue;
}
set.add(nums[i]);
path.offer(nums[i]);
backTrack(nums, i + 1);
path.removeLast();
}
}
public List<List<Integer>> findSubsequences(int[] nums) {
this.backTrack(nums, 0);
return this.ans;
}
}
全排列
题目详细:LeetCode.46
全排列转化成树形结构之后,思路就非常明辽了:
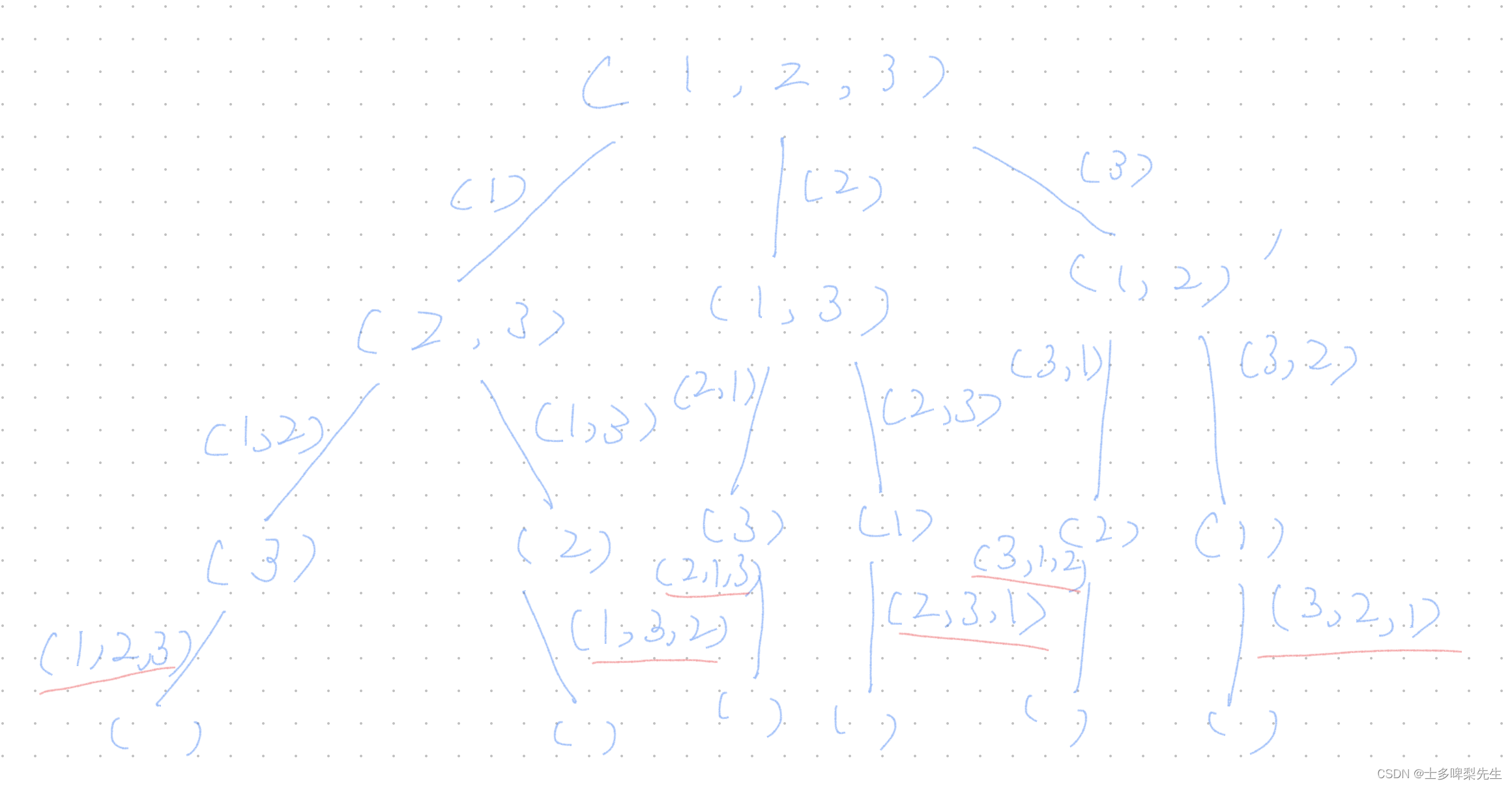
通过树形结构的叶子节点,也就是递归的结束条件可知,就是当 nums.length == 0 时,即可得到一个路径上的排列结果。
与之前做的练习题不同,在同一层中,每一个的数字都可以被访问到,也没有涉及到分割问题,所以在递归参数中可以不需要定义 startIndex 来控制从哪个下标开始访问。
所以我们可以模拟对该树形结构进行深度优先遍历得到下面的解法:
Java解法(递归,回溯,模拟):
import java.nio.*;
class Solution {
List<List<Integer>> ans = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
public int[] linkNums(int[] nums_l, int[] nums_r){
IntBuffer intbuffer = IntBuffer.allocate(nums_l.length + nums_r.length);
intbuffer.put(nums_l);
intbuffer.put(nums_r);
return intbuffer.array();
}
public int[] linkBetNums(int[] nums, int index){
int[] nums_l = Arrays.copyOfRange(nums, 0, index);
int[] nums_r = Arrays.copyOfRange(nums, index + 1, nums.length);
return this.linkNums(nums_l, nums_r);
}
public void backTrack(int[] nums){
if(nums.length == 0){
ans.add(new ArrayList<>(path));
return;
}
for(int i = 0; i < nums.length; i++){
path.offer(nums[i]);
backTrack(this.linkBetNums(nums, i));
path.removeLast();
}
}
public List<List<Integer>> permute(int[] nums) {
this.backTrack(nums);
return this.ans;
}
}
不过这样的模拟解法,看起来还是蛮多代码的,这是因为我们为了使数组nums 最后能够通过递归结束条件 nums.length == 0 ,所以多定义了两个方法,使得在每一次递归中都传递的分割后的新数组来进行操作。
但通过排列结果我们可以发现,其实可以不用这样做,递归的结束条件还可以是 path.length() == nums.length,只不过我们需要额外定义一个布尔数组used ,来标识我们每一次递归中(树的深度优先遍历)那些已经被排列的数字的下标,避免重复在排列中出现。
Java解法(递归,回溯,哈希):
class Solution {
List<List<Integer>> ans = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
public void backTrack(int[] nums, boolean[] used){
if(nums.length == path.size()){
ans.add(new ArrayList<>(path));
return;
}
for(int i = 0; i < nums.length; i++){
if(used[i]){
continue;
}
path.offer(nums[i]);
used[i] = !used[i];
backTrack(nums, used);
path.removeLast();
used[i] = !used[i];
}
}
public List<List<Integer>> permute(int[] nums) {
boolean[] used = new boolean[nums.length];
this.backTrack(nums, used);
return this.ans;
}
}
全排列 II
题目详细:LeetCode.47
在 46.全排列 中已经详细讲解了排列问题的写法,在 40.组合总和II 和 90.子集II中又详细讲解了去重的写法,话不多说,先画个图:
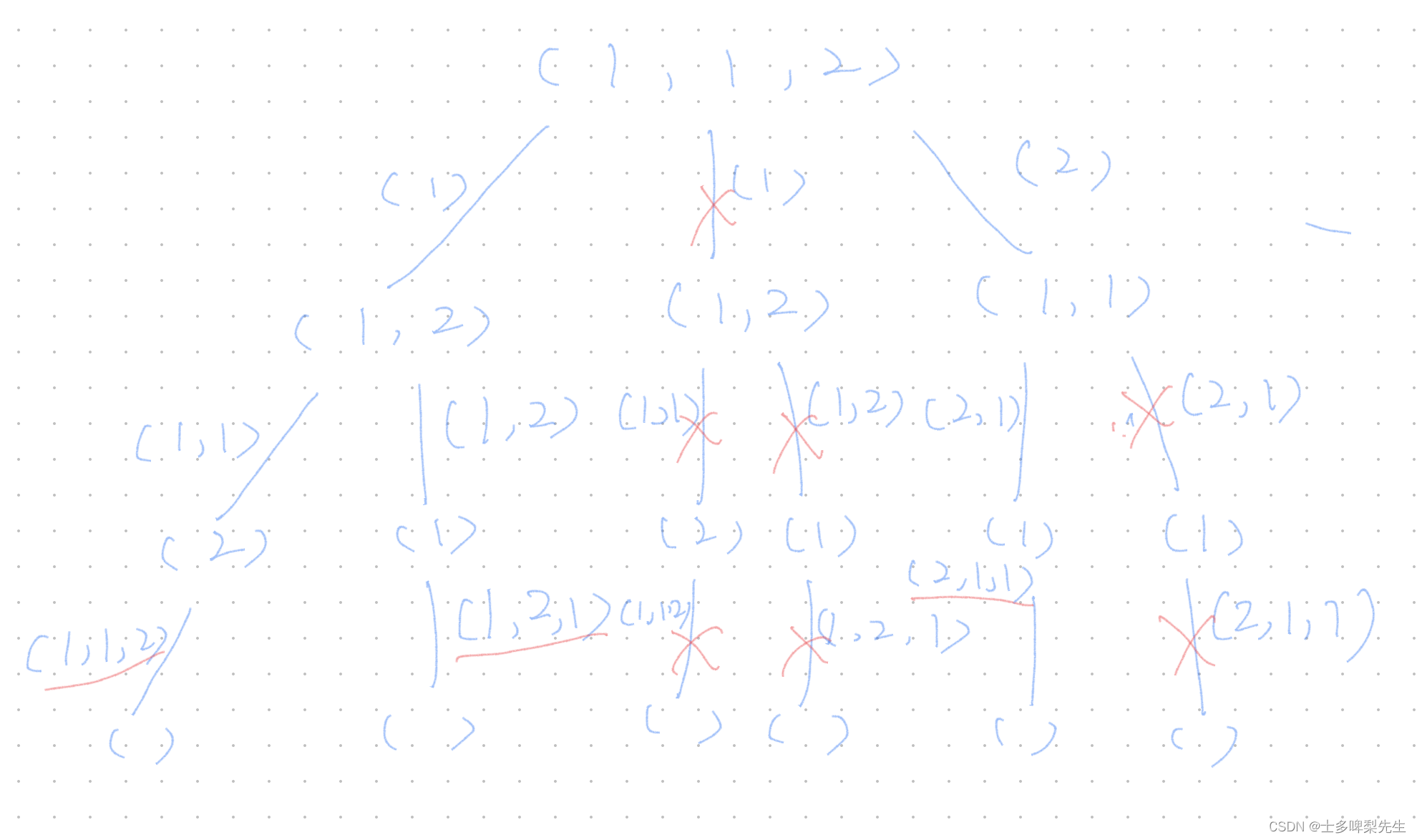
通过树形结构可知,这道题就是在上一题的基础上,加上去重的操作:
- 经过之前的题目中的去重练习,我们可以利用布尔数组used来跳过那些相同且已经被回溯的数字(即已经得到该数字开头的所有全排列结果),来进行去重
- 而且对于组合问题和排列问题进行去重,一定要对元素进行排序,这样可以方便地得知相邻的数字是否是重复的
- 去重的具体思路如下:
- 在宽度遍历到下标
i>0的数字时,就与之前一个数字做比较,如果两者相等nums[i] == nums[i - 1],且前一个数字已经被回溯used[i-1] == false,说明该数字开头的所有排列结果都已得到并添加到结果集中 - 直接
continue跳过相同的数字,继续循环直到遇到不相同的数字,进行递归继续收集其全排列结果。
- 在宽度遍历到下标
Java解法(递归,回溯,哈希):
class Solution {
List<List<Integer>> ans = new ArrayList<>();
Deque<Integer> path = new ArrayDeque<>();
public void backTrack(int[] nums, boolean[] used){
if(nums.length == path.size()){
ans.add(new ArrayList<>(path));
return;
}
for(int i = 0; i < nums.length; i++){
// used[i]:跳过在深度中已排列过的数字的下标
// i > 0 && nums[i] == nums[i - 1] && !used[i - 1]:跳过在宽度中已排列过的数字
if(used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])){
continue;
}
path.offer(nums[i]);
used[i] = !used[i];
backTrack(nums, used);
path.removeLast();
used[i] = !used[i];
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
Arrays.sort(nums);
boolean[] used = new boolean[nums.length];
this.backTrack(nums, used);
return this.ans;
}
}
做了这几道练习题之后,不难发现:
- ▲组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果。
- 有回溯必有递归,回溯的条件即是递归结束的条件
- 树形结构的宽度,与循环的次数有关
- 树形结构的深度,与递归的次数有关
- 递归的深度,相当于循环的嵌套层数
- ▲递归的深度由结束条件决定,和树的深度由树的叶子节点决定一样的道理,所以也可以说在回溯算法中,树的深度与递归的结束条件有关,换而言之,要想知道什么时候将路径上的结果加入结果集,只需要关心递归的结束条件即可。
- ▲循环的次数由循环的起始下标和循环体中的逻辑决定,主要处理的树形结构中同一层的元素访问逻辑,所以对结果去重主要是在循环体内,递归前进行。