线性表 链表表示

news2024/9/26 3:30:44

初识链表

  • 用一组物理位置任意的存储单元来存放线性表的数据元素。
  • 这组存储单元既可以是连续的，也可以是不连续的，甚至是零散分布在内存中的任意位置上的。
  • 链表中元素的逻辑次序和物理次序不一定相同。

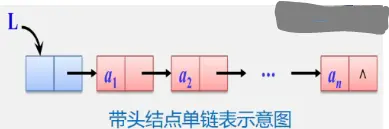
在存储自己内容的同时也存储下一个元素的地址。存储数据元素的域称为数据域，存储直接后继位置的域称为指针域。指针域中存储的信息称作指针或链。这两部分信息组成ai的存储映象称为结点(Node)。n个结点(ai(1≤i≤n)的存储映象链结成一个链表，即为线性表。把链表中第1个结点的存储位置叫头指针。最后一个元素意味着没有直接后继规定最后一个结点指针为空(通常用NULL或^表示)

单链表由头指针唯一确定，因此单链表可用头指针名字来命名。

单链表、双向链表、循环链表 其他基础辨析

结点只有一个指针域的链表称为单链表或线性链表

img

结点有两个指针域的链表称为双链表

img

首尾相接的链表叫循环链表

img

为了更加方便对链表进行操作，会在单链表的第1个结点前附设一个头结点.头结点的数据域可以不存储任何信息，也可以存储如线性表的长度等附加信息，头结点的指针域存储指向线性表第1个元素的结点。

img

头指针：

指链表指向第一个结点的指针，若链表有头结点，则是指向头结点的指针;

头指针具有标识作用，所以常用头指针冠以链表的名字;

无论链表是否为空，头指针均不为空。头指针是链表的必要元素

头结点：

头结点是为了操作的统一和方便而设立的，放在第一元素的结点之前，其数据域一般无意义（也可存放链表的长度）

有了头结点，对在第一元素结点前插入结点和删除第一结点，其操作与其它结点的操作就统一了

头结点不一定是链表必须要素

首元结点：

是指链表中存储第一个数据元素a1的结点

思考

如何表示空表

img

  • 无头结点时，头指针为空时表示空表

  • 有头结点时，当头结点的指针域为空时表示空表

有头结点有什么好处？

①有了头结点，对在第一元素结点前插入结点和删除第一结点，其操作与其它结点的操作就统一了

②便于空表和非空表的统一处理
当链表不设头结点时，假设L为单链表的头指针，它应该指向首元结点，则当单链表为长度n为0的空表时，L指针为空（判定空表的条件可记为：L == NULL)。增加头结点后，无论链表是否为空，头指针都是指向头结点的非空指针。头指针指向头结点。若为空表，则头结点的指针域为空（判定空表的条件可记为：L ->next == NULL)

链表（链式存储结构）的特点

  1. 结点在存储器中的位置是任意的，即逻辑上相邻的数据元素在物理上不一定相邻。
  2. 访问时只能通过头指针进入链表，并通过每个结点的指针域依次向后顺序扫描其余结点，所以寻找第一个结点和最后一个结点所花费的时间不等

  • 顺序表→随机存取

  • 链表→顺序存取

img

img

单链表基本操作实现

单链表的初始化（带头结点的单链表）

  • 即构造一个空表

步骤：

  1. 生成新结点作头结点，用头指针L指向头结点

  2. 将头结点的指针域置空

 Status InitList(LinkList &L) {	 //构造一个空的单链表L
        L = new LNode;        	 //生成新结点作为头结点，用头指针L指向头结点
        L->next = NULL;          //头结点的指针域置空
        return OK;
    }

补充单链表的几个常用简单算法

自我感觉除了判空都没啥用

判断链表是否为空

int ListEmpty(LinkList L)  //若L为空表，则返回1，否则返回0
{
	if(L->next) //非空
	return 0;
	else 
	return 1;
}

单链表的销毁

链表销毁后不存在

  • 从头指针开始依次释放所有结点
void DestoryList(Lnode* L)
{
	Lnode* p;
	while (L) 
	{
		p = L;
		L = L->next;
		free(p);
	}
	return;
}

清空单链表

链表仍存在，但链表中无元素，成为空链表（头指针和头结点仍然在）

  • 依次释放所有结点，并将头结点指针域设置为空

image-20230301142222821

void ClearList(Lnode* L)
{
	Lnode* p, * q;
	p = L->next;
	while (p)
	{
		q = p->next;
		free(p);
		p = q;
	}
	L->next = NULL;
}

求单链表的表长

  • 从首元结点开始，依次计数
int ListLength(Lnode* L)
{
	int i = 0;
	Lnode* p = L->next;  //p指向第一个结点
	while (p)
	{
		i++;
		p = p->next;
	}
	return i;
}

取值——取单链表第i个元素

  • 从链表的头指针出发，顺着链域next逐个结点往下搜索，直至搜索到第i个结点为止。因此，链表不是随机存取结构。
/*初识条件：顺序线性表L已存在，1 ≤ i ≤ListLength(L)
  操作结构：用e返回L中第i个数据元素的值。
*/
int GetElem(LinkList L, int i, int* e)
{
	int j;
	Lnode* p;    //声明一结点p
	p = L->next;    //让p指向链表L的第一个结点
	j = 1;          //j为计数器
	while (p && j < i )   //p不为空或者计数器j还没有等于i时循环继续
	{
		p = p->next;  //让p指向下一个结点
		j++;
	}

	if (!p || j > i)
	{
		return -1;  //第i个元素不存在
	}

	*e = p->data;    //取第i个元素的数据
	return *e;
}

算法分析：

该算法的基本操作是比较 j 和 i 并后移指针 p，while循环体中的语句频度与位置 i 有关。若 1 ≤ i ≤ n ，则频度为 i - 1 ，一定能取值成功；若 i ＞ n，则频度为n，取值失败。因此取值算法的时间复杂度为O(n)。

假设每个位置上的元素取值概率相等，即：pi = 1/n

则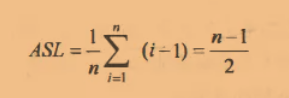：image-20230301230203501

按值查找——根据特定数据获取该数据所在地址

  1. 从第一个及诶点依次与e比较
  2. 如果找到一个与e相等的元素，则返回在列表中的地址
  3. 如果查边整个链表都没有找到和e相等的元素停止循环，并返回
Lnode* LocateElem(LinkList L, int e)
{
	// 在线性表L中查找值为e的数据元素
	//找到，则返回L中值为e的数据元素的地址，查找失败返回NULL（因为p最后指向了NULL）
	Lnode* p;
	p = L->next;
	while (p && p->data != e)
	{
		p = p->next;
	}
	return p;
}

返回该数据位置序号

相当于多加了个计数器而已

int LocateElem2(LinkList L, int e)
{
	//返回L中值为e的数据元素的位置序号，查找失败返回0
	Lnode* p;
	p = L->next;
	int j = 1;
	while (p && p->data != e)
	{
		p = p->next; 
		j++;
	}
	if (p) return j;
	else return -1;
}

该算法的执行时间与待查找的值e相关， 其平均时间复杂度分析类似于算法2.7,也为O(n)。

单链表的插入

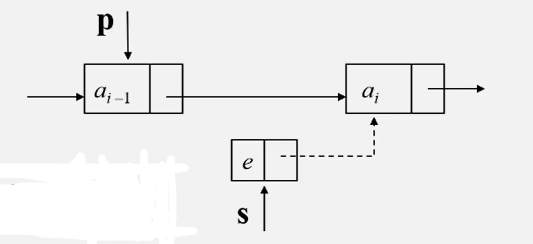
  1. 首先找到ai-1的存储结构p。
  2. 生成一个数据域为e的新结点s。
  3. 插入新结点：
    • 新结点的指针域指向结点ai s->next = p->next
    • 结点ai-1的指针域指向新结点 p->next = s;

image-20230301234735126

/*i表示插入第几个元素之前
最后L要+1*/
void ListInsert(LinkList L,int i ,int e)
{
	int j;
	Lnode* p, * s;
	p = L;    //查找算法从首元素开始p=L->next;j=1【插入算法i=1它的前一个结点的头结点j=i-1不循环】
	j = 0;
	while (p && j < i - 1)
	{
		p = p->next;
		j++;
	}
	if (!p || j > i - 1)
	{
		printf("error");//插入错误，，，并提示
		return;
	}
	s = (Lnode*)malloc(sizeof(Lnode));
	s->data = e;
	s->next = p->next;   
	p->next = s;
	return;
}

单链表的删除

按位删除

  1. 找到第i-1个结点，如果有必要的话保存ai的值且将地址存于在q中以被释放
  2. 找到ai-1的位置赋值给ai-1的next域
  3. 释放ai

p->next = p->next->next

img

/*删除L的第i个数据元素，并用e返回其值，L的长度减1*/
void Listdelete(LinkList L, int i, int* e)
{
	int j;
	Lnode* p, * q;
	p = L; //*i=1，p是头结点p=L;
	j = 0;
	while (p->next && j < i - 1)//遍历寻找第i-1个元素
	{
		p = p->next;
		j++;
	}
	if (!(p->next) || j > i - 1)
	{
		/*  printf("")  */
		return;  //第i个元素不存在，并提示
	}
	q = p->next;
	p->next = p->next->next; //或者p->next=q->next 
	*e = q->data;
	free(q);

}

按值删除

/*按值删除*/
void ListdeleteElem(LinkList L, int e)
{
	//先查找   有才能删
	//需要另写一个定位函数
	int index = find(L, e);
	if (index == -1)
	{
		//没找到
	}
	else {
		//定位到前一个元素
		Lnode* temp;
		temp = L;
		int i = 0;
		while (i < index)//定位置
		{
			temp = temp->next;
			i++;
		}

		Lnode* free_node = temp->next;
		temp->next = temp->next->next;
		free(free_node);
	}
}

int find(LinkList L, int key)
{  //定位函数，定位到待删除元素的前一个
	Lnode* temp;
	int i = 0;
	temp = L->next;
	while (temp != NULL)
	{
		if (temp->data == key)
		{
			return i;
		}
		temp = temp->next;
		i++;
	}
	return -1;
}

头插法 &尾插法建立单链表

头插法 – 元素插入在链表头部 （前插法）

  1. 从一个空表开始，重复读入数据；
  2. 生成新结点，将读入数据存放到新结点的数据域中
  3. 从最后一个结点开始，依次将各结点插入到链表的前端

img

img

/*头插法*/
void Linkinsert_head(LinkList L, int e)
{
	Lnode* temp = (Lnode*)malloc(sizeof(Lnode));// 创建新结点
	//if判断malloc是否分配成功
	temp->next = L->next;
	L->next = temp;
	temp->data = e;
}
	/*当然也可以考虑加个循环，连续插入*/

尾插法

  1. 从一个空表L开始，将新结点逐个插入到链表的尾部，尾指针r指向链表的尾结点。
  2. 初始时，r同L均指向头结点。每读入一个数据元素则申请一个新结点，将新结点插入到尾结点后，r指向新结点。
/*尾插法*/
void Linkinsert_tail(LinkList L, int e)
{
	Lnode* temp = (Lnode*)malloc(sizeof(Lnode));// 创建新结点
	temp->next = NULL;
	Lnode* r, *p; 
	r = L;
	p->data = e;
	p->next = NULL;
	r->next = p;// 插入到表尾
	r = p;  //r指向新尾结点
}

代码总结

#include<stdio.h>
#include<stdlib.h>

typedef struct Lnode {    //声明结点的类型和指向结点的指针类型
	int data;             //结点数据域
	struct Lnode* next;   //结点指针域
}Lnode, *LinkList;        //LinkList为指向结构体Lnode的指针类型

/*初始化  
	空链表
*/

Lnode* InitList(LinkList L)
{
	L = (Lnode*)malloc(sizeof(Lnode);
	if (L == NULL)
	{
		printf("分配失败");  //提示分配失败
	}
	else 
	{
		L->next = NULL;
	}
	return L;
}


void DestoryList(Lnode* L)
{
	Lnode* p;
	while (L) {
		p = L;
		L = L->next;
		free(p);
	}
	return;
}

void ClearList(Lnode* L)
{
	Lnode* p, * q;
	p = L->next;
	while (p)
	{
		q = p->next;
		free(p);
		p = q;
	}
	L->next = NULL;
}

int ListLength(Lnode* L)
{
	int i = 0;
	Lnode* p = L->next;  //p指向第一个结点
	while (p)
	{
		i++;
		p = p->next;
	}
	return i;
}

/*初识条件：顺序线性表L已存在，1 ≤ i ≤ListLength(L)
  操作结构：用e返回L中第i个数据元素的值。
*/
int GetElem(LinkList L, int i, int* e)
{
	int j;
	Lnode* p;    //声明一结点p
	p = L->next;    //让p指向链表L的第一个结点
	j = 1;          //j为计数器
	while (p && j < i )   //p不为空或者计数器j还没有等于i时循环继续
	{
		p = p->next;  //让p指向下一个结点
		j++;
	}

	if (!p || j > i)
	{
		return -1;  //第i个元素不存在
	}

	*e = p->data;    //取第i个元素的数据
	return *e;
}
/*按值查找*/
Lnode* LocateElem(LinkList L, int e)
{
	// 在线性表L中查找值为e的数据元素
	//找到，则返回L中值为e的数据元素的地址，查找失败返回NULL（因为p最后指向了NULL）
	Lnode* p;
	p = L->next;
	while (p && p->data != e)
	{
		p = p->next;
	}
	return p;
}

/*按值查找2   返回位置序号*/
int LocateElem2(LinkList L, int e)
{
	//返回L中值为e的数据元素的位置序号，查找失败返回0
	Lnode* p;
	p = L->next;
	int j = 1;
	while (p && p->data != e)
	{
		p = p->next; 
		j++;
	}
	if (p) return j;
	else return -1;
}

/*i表示插入第几个元素之前
最后L要+1*/
void ListInsert(LinkList L,int i ,int e)
{
	int j;
	Lnode* p, * s;
	p = L;    //查找算法从首元素开始p=L->next;j=1【插入算法i=1它的前一个结点的头结点j=i-1不循环】
	j = 0;
	while (p && j < i - 1)
	{
		p = p->next;
		j++;
	}
	if (!p || j > i - 1)
	{
		printf("error");//插入错误，，，并提示
		return;
	}
	s = (Lnode*)malloc(sizeof(Lnode));
	s->data = e;
	s->next = p->next;   
	p->next = s;
	return;
}

/*按位删除
删除L的第i个数据元素，并用e返回其值，L的长度减1*/
void Listdelete(LinkList L, int i, int* e)
{
	int j;
	Lnode* p, * q;
	p = L; //*i=1，p是头结点p=L;
	j = 0;
	while (p->next && j < i - 1)//遍历寻找第i-1个元素
	{
		p = p->next;
		j++;
	}
	if (!(p->next) || j > i - 1)
	{
		/*  printf("")  */
		return;  //第i个元素不存在，并提示
	}
	q = p->next;
	p->next = p->next->next; //或者p->next=q->next 
	*e = q->data;
	free(q);

}

/*按值删除*/
void ListdeleteElem(LinkList L, int e)
{
	//先查找   有才能删
	//需要另写一个定位函数
	int index = find(L, e);
	if (index == -1)
	{
		//没找到
	}
	else {
		//定位到前一个元素
		Lnode* temp;
		temp = L;
		int i = 0;
		while (i < index)//定位置
		{
			temp = temp->next;
			i++;
		}

		Lnode* free_node = temp->next;
		temp->next = temp->next->next;
		free(free_node);
	}
}

int find(LinkList L, int key)
{  //定位函数，定位到待删除元素的前一个
	Lnode* temp;
	int i = 0;
	temp = L->next;
	while (temp != NULL)
	{
		if (temp->data == key)
		{
			return i;
		}
		temp = temp->next;
		i++;
	}
	return -1;
}

/*头插法*/
void Linkinsert_head(LinkList L, int e)
{
	Lnode* temp = (Lnode*)malloc(sizeof(Lnode));// 创建新结点
	//if判断malloc是否分配成功
	temp->next = L->next;
	L->next = temp;
	temp->data = e;
}
	
/*尾插法*/
void Linkinsert_tail(LinkList L, int e)
{
	Lnode* temp = (Lnode*)malloc(sizeof(Lnode));// 创建新结点
	temp->next = NULL;
	Lnode* r, *p; 
	r = L;
	p->data = e;
	p->next = NULL;
	r->next = p;// 插入到表尾
	r = p;  //r指向新尾结点
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/382217.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Adobe illustrator使用教程

Adobe illustrator使用教程

抓手工具&#xff1a;绘制大型图片拖动图片 画放大缩小&#xff1a;Alt鼠标滚轮 间接选择工具&#xff1a;点击图标shift 进行多个对象选择&#xff0c;再次点击取消选择&#xff08;用于对多个对象进行批量操作&#xff09; 直接选择工具&#xff1a;可以对图案本身进行精细选…
阅读更多...
（二十二）操作系统-生产者·消费者问题

（二十二）操作系统-生产者·消费者问题

文章目录一、问题描述二、问题分析三、PV操作题目分析步骤1. 关系分析2. 整理思路3. 设置信号量4. 编写代码四、能否改变相邻P、V操作的顺序?五、小结1. PV操作题目的解题思路2. 注一、问题描述 系统中有一组生产者进程和一组消费者进程&#xff0c;生产者进程每次生产一个产品…
阅读更多...
什么是文件传输中台？

什么是文件传输中台？

企业文件传输的场景有哪些&#xff1f; 企业日常办公中无时无刻不在产生数据文件。多样化的数据已成为企业的重要资产&#xff0c;更被称为是“新石油”。数据并不是单单存储起来就行了&#xff0c;而是需要高效又安全的让数据流转起来&#xff0c;释放其自身的价值&#xff0…
阅读更多...
XGBoost和LightGBM时间序列预测对比

XGBoost和LightGBM时间序列预测对比

XGBoost和LightGBM都是目前非常流行的基于决策树的机器学习模型&#xff0c;它们都有着高效的性能表现&#xff0c;但是在某些情况下&#xff0c;它们也有着不同的特点。 XGBoost和LightGBM简单对比 训练速度 LightGBM相较于xgboost在训练速度方面有明显的优势。这是因为Ligh…
阅读更多...
发票自动OCR识别并录入模板 3分钟免费配置

发票自动OCR识别并录入模板 3分钟免费配置

要问整个公司里和数据打交道最多的职能&#xff0c;非财务莫属了吧。除了每天要处理大量财务数据外&#xff0c;还有发票录入的工作让财务陷入“易燃易爆炸”的工作状态。发票报销看似简单&#xff0c;但发票的类型有很多种&#xff0c;每种发票需要录入的信息也有差别。再加上…
阅读更多...
SimpleITK 获取CT spacing 底层原理

SimpleITK 获取CT spacing 底层原理

SimpleITK 获取CT spacing 底层原理 一、层厚、层间距概念 层厚&#xff1a; CT扫描机扫描出来的断层的层的厚度&#xff0c; 通常用Slice thickness表示&#xff0c; 比如 5mm 层间隔&#xff1a;一般用 Slice interval 或 Slice increment来表示&#xff0c;比如 5mm。在 …
阅读更多...
最新！蔚来2022年第四季度被理想汽车超越，或将在2023年全面落后

最新！蔚来2022年第四季度被理想汽车超越，或将在2023年全面落后

3月1日&#xff0c;蔚来汽车&#xff08;NYSE: NIO; HKEX: 9866; SGX: NIO&#xff0c;下称“蔚来”&#xff09;发布了截至2022年12月31日的第四季度及全年财报。财报显示&#xff0c;蔚来2022年第四季度实现营收160.64亿元&#xff08;约23.29亿美元&#xff09;&#xff0c;…
阅读更多...
SpringBoot实现静态资源映射，登录功能以及访问拦截验证——以黑马瑞吉外卖为例

SpringBoot实现静态资源映射，登录功能以及访问拦截验证——以黑马瑞吉外卖为例

目录 一、项目简介 二、设置静态资源访问路径 三、实现登录功能 四、拦截访问请求 本篇文章以黑马瑞吉外卖为例 一、项目简介 瑞吉外卖项目分为后台和前台系统&#xff0c;后台提供给管理人员使用&#xff0c;前台则是用户订餐使用 资源我们放在resources下 二、设置静态…
阅读更多...
Postman的下载和安装

Postman的下载和安装

文章目录一 下载二 安装一 下载 官网下载地址&#xff1a;https://www.postman.com/ 进入官网页面&#xff0c;选择对应的操作系统和版本&#xff0c;然后进入Postman下载页面&#xff0c;然后点击 Windows 64-bit 即可下载&#xff0c;如下 二 安装 Postman的安装很简单&am…
阅读更多...
Python每日一练(20230302)

Python每日一练(20230302)

目录 1. 字符串统计 2. 合并两个有序链表 3. 下一个排列 附录 Python字典内置方法 增 删 改 查 其它 1. 字符串统计 从键盘输入一个包含有英文字母、数字、空格和其它字符的字符串&#xff0c;并分别实现下面的功能&#xff1a;统计字符串中出现2次的英文字母&#…
阅读更多...
C++---最长上升子序列模型---友好城市（每日一道算法2023.3.2）

C++---最长上升子序列模型---友好城市（每日一道算法2023.3.2）

注意事项&#xff1a; 本题为"线性dp—最长上升子序列的长度"的扩展题&#xff0c;所以dp思路这里就不再赘述。 题目&#xff1a; Palmia国有一条横贯东西的大河&#xff0c;河有笔直的南北两岸&#xff0c;岸上各有位置各不相同的N个城市。 北岸的每个城市有且仅有…
阅读更多...
python自学之《21天学通Python》(18)——第21章 案例2 Python搞定大数据

python自学之《21天学通Python》(18)——第21章 案例2 Python搞定大数据

“大数据&#xff08;Big Data&#xff09;”这个术语最早期的引用可追溯到apache org的开源项目Nutch。当时&#xff0c;大数据用来描述为更新网络搜索索引需要同时进行批量处理或分析的大量数据集。随着谷歌MapReduce和GoogleFileSystem &#xff08;GFS&#xff09;的发布&a…
阅读更多...
第十三节 继承

第十三节 继承

什么是继承&#xff1f; java中提供一个关键字extends&#xff0c;用这个关键字&#xff0c;我们可以让一个类和另一个类建立父子关系。 public class Student extends People{} student为子类&#xff08;派生类&#xff09;&#xff0c;people为父类&#xff08;基类或者超类…
阅读更多...
激光雷达迈向规模量产期：如何看待3类玩家的竞争格局？

激光雷达迈向规模量产期：如何看待3类玩家的竞争格局？

激光雷达正进入规模量产周期。 高工智能汽车研究院监测数据显示&#xff0c;2022年中国市场&#xff08;不含进出口&#xff09;乘用车前装标配激光雷达交付12.99万颗&#xff0c;配套新车11.18万辆&#xff0c;同比分别增长1544.30%和2626.82%&#xff1b;预计2023年标配交付将…
阅读更多...
第四回：文字图例尽眉目

第四回：文字图例尽眉目

import matplotlib import matplotlib.pyplot as plt import numpy as np import matplotlib.dates as mdates import datetime一、Figure和Axes上的文本 Matplotlib具有广泛的文本支持&#xff0c;包括对数学表达式的支持、对栅格和矢量输出的TrueType支持、具有任意旋转的换…
阅读更多...
Python进阶-----面向对象2.0（特有属性和方法与私有属性和方法）

Python进阶-----面向对象2.0（特有属性和方法与私有属性和方法）

目录 前言&#xff1a; 1.添加特有属性/方法 示例1&#xff1a;添加特有属性 示例2&#xff1a;添加特有方法 2.私有属性/方法 &#xff08;1&#xff09;私有化示例 &#xff08;2&#xff09; 私有化属性/方法可以在类的内部使用 &#xff08;3&#xff09;强制访问私…
阅读更多...
一：BT、BLE版本说明及对比

一：BT、BLE版本说明及对比

蓝牙版本说明1.常见名词说明2.BT&BLE特性对比3.BT各版本对比4.BLE各版对比1.常见名词说明 名称说明BR(Basic Rate)基本码率EDR(Enhanced Data Rate)增强码率BLE(Bluetooth Low Energy)低功耗蓝牙HS(High Speed)高速蓝牙BT(BlueTooth)蓝牙技术LE(Low Energy)低能耗AFH(Adap…
阅读更多...
态路小课堂丨光模块使用可能遇到的4大问题以及注意事项！

态路小课堂丨光模块使用可能遇到的4大问题以及注意事项！

光模块作为光通信系统的核心器件&#xff0c;其内部集成了精密的光学元件和电路元件。在日常使用过程中如果不按规定操作&#xff0c;很容易导致光模块损坏。本文态路通信为您介绍光模块在使用时可能遇到的问题&#xff0c;以及我们应该注意的事项。以此来减少光模块使用寿命&a…
阅读更多...
Spring 事务（编程式事务、声明式事务@Transactional、事务隔离级别、事务传播机制）

Spring 事务（编程式事务、声明式事务@Transactional、事务隔离级别、事务传播机制）

文章目录1. 事务的定义2. Spring 中事务的实现2.1 MySQL 中使用事务2.2 Spring 中编程式事务的实现2.3 Spring 中声明式事务2.3.1 声明式事务的实现 Transactional2.3.2 Transactional 作用域2.3.3Transactional 参数设置2.3.4 Transactional 异常情况2.3.5 Transactional 工作…
阅读更多...
桑基图绘制

桑基图绘制

绘制桑基图 但是关于数据流上的数据标签可能还得用ps… 注意 1、节点&#xff08;nodes&#xff09;要包括各层的&#xff0c;且不能重复&#xff0c;需要自己在后边append几个数据 2、数据流的数据要是整数&#xff0c;不能时numpy 3、注意表格加入时要再由array转为list&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023