注意事项:
本题为"线性dp—最长上升子序列的长度"的扩展题,所以dp思路这里就不再赘述。
题目:
Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的N个城市。
北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。
编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。
输入格式
第1行,一个整数N,表示城市数。
第2行到第n+1行,每行两个整数,中间用1个空格隔开,分别表示南岸和北岸的一对友好城市的坐标。
输出格式
仅一行,输出一个整数,表示政府所能批准的最多申请数。
数据范围
1≤N≤5000,
0≤xi≤10000
输入:
7
22 4
2 6
10 3
15 12
9 8
17 17
4 2
输出:
4
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010;
pair<int, int> w[N];
int f[N];
int n;
//最长上升子序列模板,返回长度
int lis() {
int res = 0;
for (int i = 1; i<=n; i++) {
f[i] = 1;
for (int j = 1; j<i; j++) {
if (w[j].second < w[i].second) f[i] = max(f[i], f[j] + 1);
}
res = max(res, f[i]);
}
return res;
}
int main()
{
//读入
cin >> n;
for (int i = 1; i<=n; i++) cin >> w[i].first >> w[i].second;
//pair的排序默认就是按照第一个元素的大小由小到大,我这里写出来是复习一下, 大家直接sort(w+1, w+n+1)即可
sort(w+1, w+n+1, [](auto a, auto b){return a.first < b.first;});
cout << lis();
return 0;
}
思路:
这道题的代码很简单,难点在于对于题目思路的转换
首先分析重点:
1.每个城市只能建一座桥
2.桥与桥不能相交
目标:问最多能建多少座桥
可以画出这样一个图:
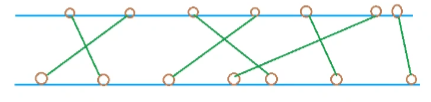
图中的圆圈就是城市,每个城市在对岸都有其对应的友好城市,以绿线连接。
到这里就能看出一个重要性质了,将某一侧的城市位置进行排序后
在对岸的友好城市位置的最长上升子序列的长度 即为 桥最多能建立的数量。
这个性质是需要一些纯经验或者看脑袋的开窍程度才能在一定时间内想明白的,莫办法,多练吧呜呜呜
声明:
算法思路来源为y总,详细请见https://www.acwing.com/
本文仅用作学习记录和交流