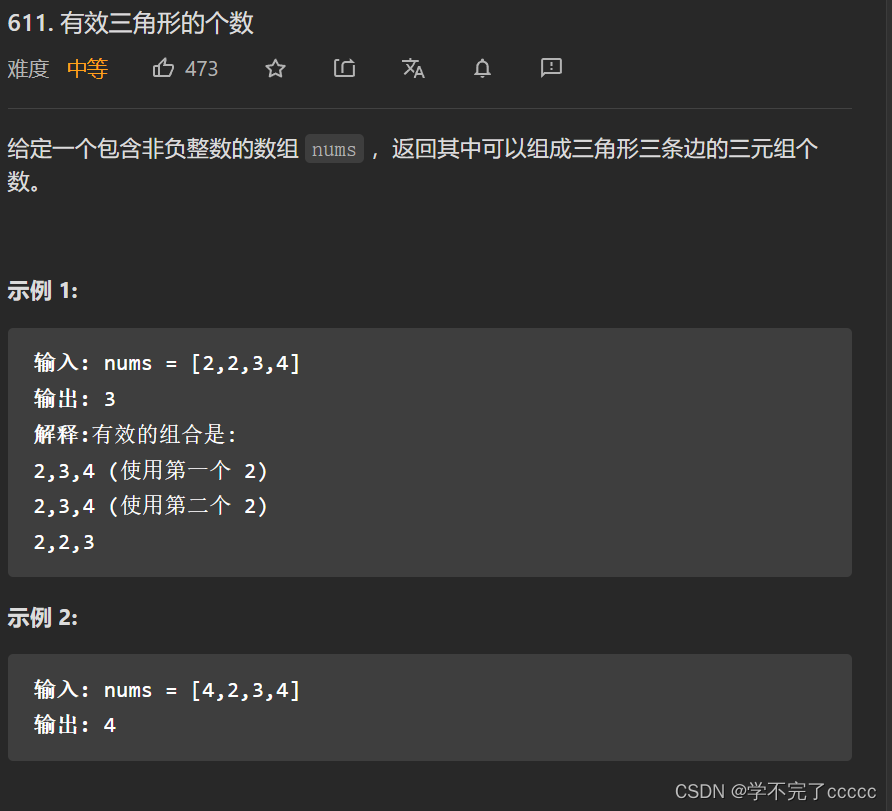
树状数组
文章目录
- 树状数组
- 引入
- 例题
- AcWing241.楼兰图腾
- 思路
- 代码
- AcWing 242. 一个简单的整数问题
- 思路
- 代码
- AcWing 244. 谜一样的牛
- 思路
- 代码
- 总结
引入
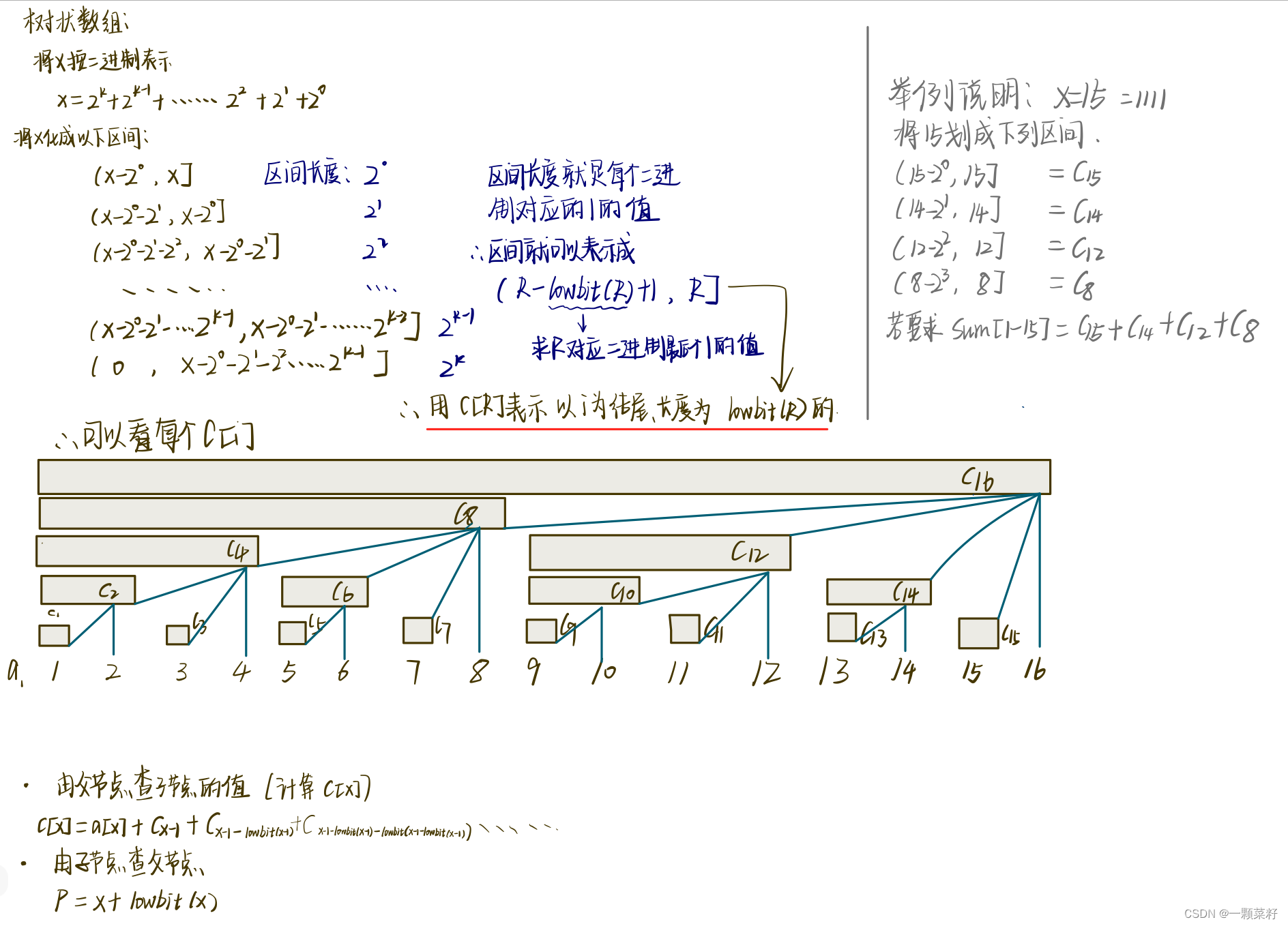
树状数组主要维护的是这样一个数据结构:
tr[x]表示以x为终点的长度为lowbit(x)的前缀和
对于树状数组主要就两种操作
- 对一段区间求解前缀和
通过合并分解后的每一段长度为相应lowbit的tr[i]求解
模板
def ask(x) :
res = 0
i = x
while i :
res += tr[i]
i -= lowbit(i)
return res
- 修改某个数
通过对其每一段父节点(加上lowbit)进行操作。
def add(x, c) :
i = x
while i <= n :
tr[i] += c
i += lowbit(i)
应用:
例题
AcWing241.楼兰图腾
在完成了分配任务之后,西部 314
来到了楼兰古城的西部。
相传很久以前这片土地上(比楼兰古城还早)生活着两个部落,一个部落崇拜尖刀(V),一个部落崇拜铁锹(∧),他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。
西部 314
在楼兰古城的下面发现了一幅巨大的壁画,壁画上被标记出了 n
个点,经测量发现这 n
个点的水平位置和竖直位置是两两不同的。
西部 314
认为这幅壁画所包含的信息与这 n
个点的相对位置有关,因此不妨设坐标分别为 (1,y1),(2,y2),…,(n,yn)
,其中 y1∼yn
是 1
到 n
的一个排列。
西部 314
打算研究这幅壁画中包含着多少个图腾。
如果三个点 (i,yi),(j,yj),(k,yk)
满足 1≤i<j<k≤n
且 yi>yj,yj<yk
,则称这三个点构成 V 图腾;
如果三个点 (i,yi),(j,yj),(k,yk)
满足 1≤i<j<k≤n
且 yi<yj,yj>yk
,则称这三个点构成 ∧ 图腾;
西部 314
想知道,这 n
个点中两个部落图腾的数目。
因此,你需要编写一个程序来求出 V 的个数和 ∧ 的个数。
输入格式
第一行一个数 n
。
第二行是 n
个数,分别代表 y1,y2,…,yn
。
输出格式
两个数,中间用空格隔开,依次为 V 的个数和 ∧ 的个数。
数据范围
对于所有数据,n≤200000
,且输出答案不会超过 int64
。
y1∼yn
是 1
到 n
的一个排列。
输入样例:
5
1 5 3 2 4
输出样例:
3 4
思路
对于V形图腾来说,可以通过枚举每一个点作为最低点时,可组成的V形序列个数,最终求和得到最终答案。
基于单个点x,我们可以先从左到右的记录其左端大于x的点个数,同理可以记录其右端大于x的点个数,二者相乘即为结果。
每次都得查询之前所有点中小于(大于)a[x]的个数,再遍历后一个点前,需要将当前点加入查询的数据结构中。
区间查询、单点修改
树状数组呼之欲出。
代码
N = 200010
a = [0] * N
def lowbit(x) :
return x & -x
def ask(x) :
res = 0
i = x
while i :
res += tr[i]
i -= lowbit(i)
return res
def add(x, c) :
i = x
while i <= n :
tr[i] += c
i += lowbit(i)
n = int(input())
a[1 : n + 1] = list(map(int, input().split()))
greater, lower = [0] * (n + 1), [0] * (n + 1)
tr = [0] * (n + 1)
# 从左到右,记录每个点左边大于/小于的情况
for i in range(1, n + 1) :
x = a[i]
greater[i] = ask(n) - ask(x)
lower[i] = ask(x - 1)
add(x, 1)
res1, res2 = 0, 0
tr = [0] * (n + 1)
# 从右到左求解结果
for i in range(n, 0, -1) :
x = a[i]
res1 += greater[i] * (ask(n) - ask(x))
res2 += lower[i] * ask(x - 1)
add(x, 1)
print(res1, res2)
AcWing 242. 一个简单的整数问题
给定长度为 N的数列 A,然后输入 M 行操作指令。
第一类指令形如 C l r d,表示把数列中第 l∼r
个数都加 d
。
第二类指令形如 Q x,表示询问数列中第 x
个数的值。
对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数 N
和 M
。
第二行包含 N
个整数 A[i]
。
接下来 M
行表示 M
条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤105
,
|d|≤10000
,
|A[i]|≤109
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2
输出样例:
4
1
2
5
思路
C表示对一定区间进行操作,Q表示对单点查询。
转化为差分
对差分数组的单点操作
≡
\equiv
≡ 对原数组的区间操作
对差分数组的区间查询
≡
\equiv
≡ 对原数组的单点查询
代码
N = 100010
a= [0] * N
tr = [0] * N
def lowbit(x) :
return x & -x
def add(x, c) :
i = x
while i <= n :
tr[i] += c
i += lowbit(i)
def ask(x) :
res = 0
i = x
while i :
res += tr[i]
i -= lowbit(i)
return res
n, m = map(int, input().split())
a[1 : n + 1] = list(map(int, input().split()))
# 初始化差分树状数组
for i in range(1, n + 1) :
add(i, a[i] - a[i - 1])
for i in range(m) :
cmd = input()
if cmd[0] == "Q" :
x = int(cmd.split()[1])
print(ask(x))
else :
l, r, c = map(int, cmd[2 :].split())
add(l, c)
add(r + 1, -c)
AcWing 244. 谜一样的牛
有 n 头奶牛,已知它们的身高为 1∼n
且各不相同,但不知道每头奶牛的具体身高。
现在这 n
头奶牛站成一列,已知第 i
头牛前面有 Ai
头牛比它低,求每头奶牛的身高。
输入格式
第 1
行:输入整数 n
。
第 2…n
行:每行输入一个整数 Ai
,第 i
行表示第 i
头牛前面有 Ai
头牛比它低。
(注意:因为第 1
头牛前面没有牛,所以并没有将它列出)
输出格式
输出包含 n
行,每行输出一个整数表示牛的身高。
第 i
行输出第 i
头牛的身高。
数据范围
1≤n≤105
输入样例:
5
1
2
1
0
输出样例:
2
4
5
3
1
思路
从后往前,最后一头牛知道自己比前
A
n
A_n
An头牛高,则最后一头牛是
A
n
+
1
A_n+1
An+1高的牛。
倒数第二头牛,知道自己比前
A
n
−
1
A_{n-1}
An−1头牛高,则当前的牛是除去
A
n
+
1
A_n+1
An+1的高度外的
A
n
−
1
+
1
A_{n-1} + 1
An−1+1的高度的牛。
由此可以递推得到所有结果。
这个过程中我们需要维护一个所有未确定高度的数据结构,我们需要对这个数据结构的操作是,查询某个高度是第几高,以及删除某点的高度。
树状数组!!!!
代码
N = 100010
tr = [0] * N
a = [0] * N
def lowbit(x) : return x & -x
def add(x, c) :
i = x
while i <= n :
tr[i] += c
i += lowbit(i)
def ask(x) :
res = 0
i = x
while i :
res += tr[i]
i -= lowbit(i)
return res
n = int(input())
for i in range(2, n + 1) :
a[i] = int(input())
for i in range(1, n + 1) :
add(i, 1)
res = [0] * (n + 1)
for i in range(n, 0, -1) :
x = a[i] + 1
# 找到一个满足第x的高度
l, r = 0, n
while l < r :
mid = (l + r) >> 1
if ask(mid) >= x :
r = mid
else :
l = mid + 1
res[i] = l
add(l, -1)
for i in range(1, n + 1) :
print(res[i])
总结
树状数组的题,一般需要发掘题目中需要的两种操作,这一点非常关键,剩下实现就肥肠煎蛋。